树上信息维护

对于树上的信息，根据操作的不同，用不同的数据结构来维护，它们是相互独立的。如果有多种操作，分开维护最后加起来就行了。

目录

一、子树加，子树求和

二、链加，单点求值

三、链加，子树求和

四、点加，链求和

五、子树加，链求和

---

一、子树加，子树求和

【口胡】

可以利用dfs序。如果记录L[i]表示i号点的dfs序，R[i]表示i号点的子树搜索完后的dfs序那么x是y的祖先等价于：

L[y]∈ [L[x],R[x]] 

dfs时用L数组记录dfn[x]，当子树搜索完后，用R数组记录R[x].如下：

void dfs(int x,int fa){
	L[x]=++sz;
	for(int i=Head[x];i;i=Next[i])
        if(V[i]!=fa)
		    dfs(V[i],x);
	R[x]=sz;
}

这时要求子树和或子树加，用线段树维护就行了。

线段树模板

二、链加，单点求值

先上个模板题

描述

有n个节点N-1条边，这是一颗树，有2个操作：

1 x y v：表示将节点x到y最短路径上所有的点的权值+v

【链加】

 

2 x：表示查询节点x的权值

【单点求值】

 

开始的时候每个节点的权值是0

输入

第一行是数N，表示N个节点 接下来n-1行，每行描述了n-1条边。

接下来是一个数q表示有q次查询与询问 接下来q行，格式如题

输出

若干行

样例输入[复制]

3
1 2
2 3
3
1 1 2 5
1 1 3 2
2 2

样例输出[复制]

7

提示

n<=1e5 q<=1e5

【口胡】

对于一个链加，我们把它看做一个点到根的路径加：

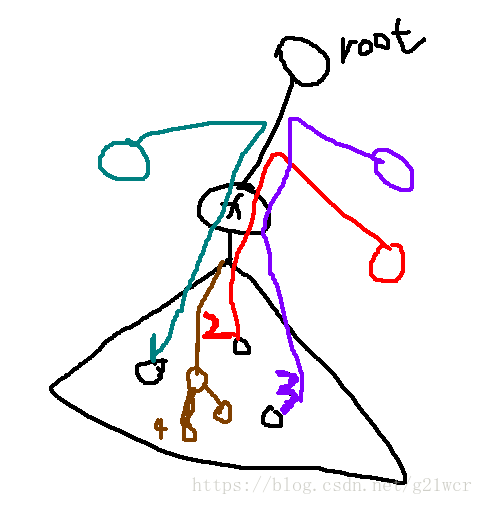
这是一条从u到v的路径，g是u和v的最近公共祖先，在这条链上加C可以看做u到root加C，然后v到root加C，然后g到root减去2*C。但是这样g点的修改就被抵消，所以用一个额外的数组app记录当一个点为lca时修改的值。

我们修改时可以把修改放在u，v和g上(单点修改)，查询时，我们就在这个点的子树中询问贡献（区间求和）。【因为一个点子树中的修改才对它有影响，其他地方的修改对它是没有贡献的】

这里用树状数组维护，支持单点修改和区间求和。【树状数组建立在DFS序上。】

假设我们查询一个点x，它的子树中有若干个修改，链1，链2，链3，链4.

对于链1，链2，链3，它们穿过了x，查询x的子树时就会把点1，点2，点3的贡献计入x中。

对于链4，虽然它在x的子树中，但是没有穿过x，所以它对x没有贡献。假设链4加上了C。

而计算时，我们计算了链4的u、v和lca(u,v)的贡献，分别是C、C、-2C，加起来就抵消了，恰好对x没有贡献。

代码：

#include<bits/stdc++.h>
#define lowbit(x) ((x)&-(x))
using namespace std;
const int maxn=100010;
int n,m,u,v,cnt=0,sz=0,op,x,y;
int Head[maxn],Next[maxn<<1],V[maxn<<1];
int f[maxn][20],L[maxn],R[maxn],dep[maxn];
int tr[maxn];
int app[maxn];
void read(int &x){
	x=0;char ch=getchar();
	while(ch>'9'||ch<'0') ch=getchar();
	while(ch<='9'&&ch>='0') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
}
void sc(int x){
	if(x>9) sc(x/10);
	putchar(x%10+48);
}
void change(int x,int v){
	if(x==0) return;
	for(;x<=n;x+=lowbit(x)) tr[x]+=v;
}

int sum(int x){
	int ret=0;
	for(;x;x-=lowbit(x)) ret+=tr[x];
	return ret;
}
	
void Add(int u,int v){
	++cnt;
	Next[cnt]=Head[u];
	V[cnt]=v;
	Head[u]=cnt;
}
void dfs(int x,int fa){
	L[x]=++sz;
	f[x][0]=fa; for(int i=1;i<19;++i) f[x][i]=f[f[x][i-1]][i-1];
	dep[x]=dep[fa]+1;
	for(int i=Head[x];i;i=Next[i])  if(V[i]!=fa)
		dfs(V[i],x);
	R[x]=sz;
}
int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=18;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=18;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}
int main(){
	read(n);
	for(int i=1;i<n;++i){
		read(u),read(v);
		Add(u,v),Add(v,u);
	}
	dfs(1,0);
	read(m);
	for(int i=1;i<=m;++i){
		read(op);
		if(op==1){
			read(x),read(y),read(v);
			int g=lca(x,y);
			change(L[x],v);
			change(L[y],v);
			change(L[g],(-2)*v);
			app[g]+=v;
		}
		if(op==2){
			read(x);
			int ans=sum(R[x])-sum(L[x]-1)+app[x];
			sc(ans);
			putchar('\n');
		}
	}
}

三、链加，子树求和

再来一发模板题

描述

有n个节点N-1条边，这是一颗树，有2个操作：

1 x y v：表示将节点x到y最短路径上所有的点的权值+v

2 x：表示查询子树x的权值和

开始的时候每个节点的权值是0

输入

第一行是数N，表示N个节点 接下来n-1行，每行描述了n-1条边。

接下来是一个数q表示有q次查询与询问 接下来q行，格式如题

输出

若干行

样例输入[复制]

3
1 2
2 3
3
1 1 2 5
1 1 3 2
2 2

样例输出[复制]

9

提示

q,n<=1e5 权值修改范围在100

 

对于链加，和刚才类似，看做一个点到根的路径加。

考虑一个修改(x,W)【x为点】，如果它对y有贡献当且仅当y为x的祖先。贡献为(dep[x]-dep[y]+1)*W。

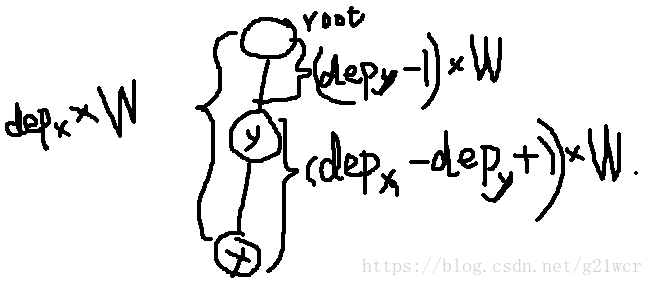
把(dep[x]-dep[y]+1)*W分解得两部分：dep[x]*W和(-dep[y]+1)*W

用两个树状数组维护这两个部分【两个部分相互独立】

用一个部分维护dep[x]*W,每次询问的时候加上就行了。

另一个部分维护W,记录每次修改的值。

询问一个点A的子树和时，求它子树中每个点dep[x]*W的和，然后求它子树中 修改的总和W×(1-dep[A])，再加起来就行了。

注意这里的修改方式：

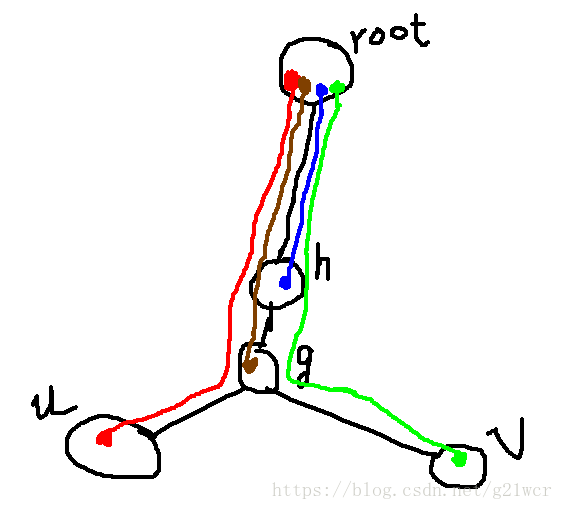
红+绿-棕-蓝，剩下的就是u到v的链，这就是一次修改。【g为lca(u,v),h为g的father】

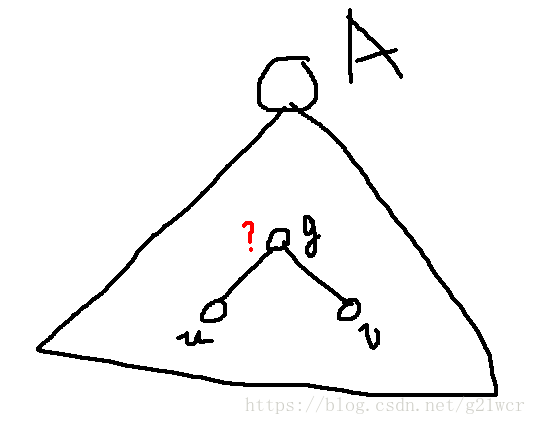
【注意这里不能用数组单独记录在lca上的修改然后lca减两次。因为询问的是子树。如下图，A不能记录子树中的lca，顶多记录以它为lca的修改。而刚才询问的是点，只需要关注它一个点就行了，所以可以记录下来。】

写完之后不要忘了dfs............

代码：

#include<bits/stdc++.h>
#define lowbit(x) (x&-(x))
using namespace std;
const int maxn=100010;
int n,m,x,y,u,v,op,cnt=0,sz=0;
int Next[maxn<<1],V[maxn<<1],Head[maxn];
int L[maxn],R[maxn],dep[maxn],f[maxn][20];
int t1[maxn],t2[maxn],app[maxn],bpp[maxn];

void change(int *tr,int x,int v){
	if(x==0) return;
	for(;x<=n;x+=lowbit(x)) tr[x]+=v;
}

int sum(int *tr,int x){
	int ret=0;
	for(;x;x-=lowbit(x)) ret+=tr[x];
	return ret;
}

void Add(int u,int v){
	++cnt;
	Next[cnt]=Head[u];
	V[cnt]=v;
	Head[u]=cnt;
}

void dfs(int x,int fa){
    L[x]=++sz;
    f[x][0]=fa;for(int i=1;i<19;i++)f[x][i]=f[f[x][i-1]][i-1];
    dep[x]=dep[fa]+1;
    for(int i=Head[x];i;i=Next[i]) if(V[i]!=fa) dfs(V[i],x);
    R[x]=sz;
}   

int lca(int x,int y) {   
    if (dep[x]<dep[y]) swap(x,y);   
    for (int i=18; i>=0; i--) if (dep[f[x][i]]>=dep[y]) x=f[x][i];   
    if (x==y) return x;   
    for (int i=18; i>=0; i--) if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];    
    return f[x][0];   
}   

void read(int &x){
	x=0;char ch=getchar();
	while(ch>'9'||ch<'0') ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
}

int main(){
	read(n);
	
	for(int i=1;i<n;++i){
		read(u),read(v);
		Add(u,v),Add(v,u);
	}
	
	dfs(1,0);
	read(m);
	for(int i=1;i<=m;++i){
		read(op);
		if(op==1){
			read(x),read(y),read(v);
			int g=lca(x,y);
			change(t1,L[x],dep[x]*v);change(t1,L[y],dep[y]*v);
			change(t1,L[g],-dep[g]*v);change(t1,L[f[g][0]],-dep[f[g][0]]*v);
			
			change(t2,L[x],v);change(t2,L[y],v);
			change(t2,L[g],-v);change(t2,L[f[g][0]],-v);
		}
		if(op==2){
			read(x);
			printf("%d\n",sum(t1,R[x])-sum(t1,L[x]-1)+(sum(t2,R[x])-sum(t2,L[x]-1))*(1-dep[x]));
		}
	}
}

四、点加，链求和

对一条链求和，可以转化为一个点到根的路径和。【和链加一样】

先考虑问题的简化版：如何求一个点到根的点权和。

一个修改(x,W)对y有贡献当且仅当x为y的祖先。所以修改一个x时，将它的子树全部修改。

 

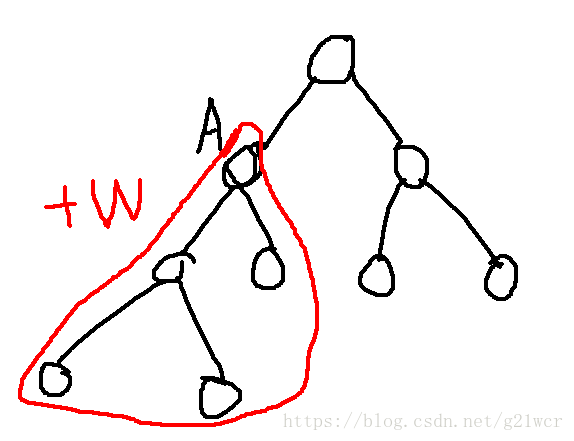
我们如果对A点加W，那么它的子孙节点到根的点权和都会加上W。建立一个线段树维护一下就行了。

修改时就是从L[A]到R[A]全部加上W，就是区间加。然后询问一个点到根节点的点权和时就是一个单点查询。

然后把这个问题转移到链求和上，就跟刚才一样，查四个点然后乱搞就行了。

 题目：

描述

有n个节点N-1条边，这是一颗树，有2个操作：

1 x v：表示将节点x的权值+v

2 x y：表示查询x到y的路径权值和

输入

第一行是数N，表示N个节点，接下一行是n个数，表示每个节点的初始权值。

接下来n-1行，每行描述了n-1条边。

接下来是一个数q表示有q次查询与询问 接下来q行，格式如题

输出

若干行

样例输入[复制]

3
1 2 3
1 2
2 3
3
1 1 2 
1 2 3 
2 1 3

样例输出[复制]

11

提示

q,n<=1e5 权值修改范围在100

 

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,m,x,y,u,v,op,cnt=0,sz=0;
int Head[maxn],Next[maxn<<1],V[maxn<<1];
int dep[maxn],L[maxn],R[maxn],f[maxn][20],w[maxn];
int lazy[maxn<<2];

void push_down(int root){
	if(lazy[root]){
		lazy[root<<1]+=lazy[root];
		lazy[root<<1|1]+=lazy[root];
		lazy[root]=0;
	}
}

void Update(int L,int R,int C,int l,int r,int root){
	if(L<=l&&R>=r){
		lazy[root]+=C;
		return;
	}
	int mid=(l+r)>>1;
	push_down(root);
	if(L<=mid) Update(L,R,C,l,mid,root<<1);
	if(R>mid)  Update(L,R,C,mid+1,r,root<<1|1);
}

int Query(int pos,int l,int r,int root){
	if(pos==0) return 0;
	if(l==r) return lazy[root];
	int mid=(l+r)>>1;
	push_down(root);
	if(pos<=mid) return Query(pos,l,mid,root<<1);
	else return Query(pos,mid+1,r,root<<1|1);
}

void read(int &x){
	x=0;char ch=getchar();
	while(ch>'9'||ch<'0') ch=getchar();
	while(ch<='9'&&ch>='0') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
}

void Add(int u,int v){
	++cnt;
	Next[cnt]=Head[u];
	V[cnt]=v;
	Head[u]=cnt;
}

void dfs(int u,int fa){
	L[u]=++sz;
	f[u][0]=fa; for(int i=1;i<19;++i) f[u][i]=f[f[u][i-1]][i-1];
	dep[u]=dep[fa]+1;
	for(int i=Head[u];i;i=Next[i]) if(V[i]!=fa) dfs(V[i],u);
	R[u]=sz;
}

int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=18;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=18;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}

int main(){
	read(n);
	for(int i=1;i<=n;++i)
		read(w[i]);
	for(int i=1;i<n;++i){
		read(u),read(v);
		Add(u,v),Add(v,u);
	}
	dfs(1,0);
	//最开始点有点权
	for(int i=1;i<=n;++i) Update(L[i],R[i],w[i],1,n,1);
	read(m);
	for(int i=1;i<=m;++i){
		read(op);
		if(op==1){
			read(x),read(v);
			Update(L[x],R[x],v,1,n,1);
		}
		if(op==2){
			read(x),read(y);
			int g=lca(x,y);
			int ansX=Query(L[x],1,n,1);
			int ansY=Query(L[y],1,n,1);
			int ansG=Query(L[g],1,n,1);
			int ansF=Query(L[f[g][0]],1,n,1);
			printf("%d\n",ansX+ansY-ansG-ansF);
		}
	}
}

五、子树加，链求和

链求和还是看做一个点到根的路径和。

一个修改(x,W)对y有贡献，当且仅当x为y的祖先。贡献为(dep[y]-dep[x]+1)*W。

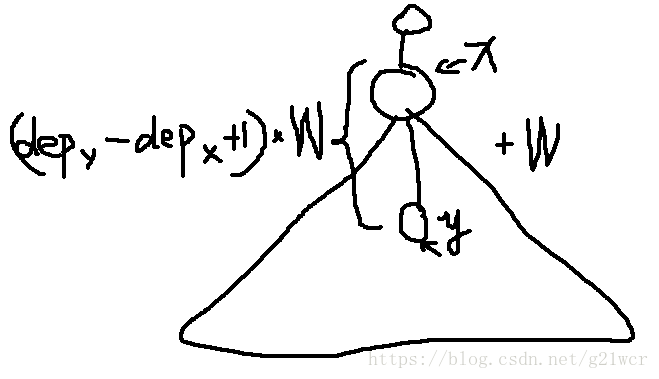
拆一下，变成 -dep[x]*W 和 (1+dep[y])*W —— (-dep[x]*W)记在L[x]到R[x]上，W也记在L[x]到R[x]上。分别维护两个区间和就行了,然后查询时就是单点查询。举个栗子：

询问y到根的距离，然后这条路径上有3个子树修改x1，x2，x3，修改值分别为w1，w2，w3。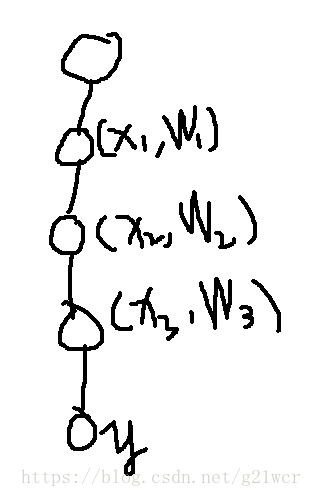

那么询问y得到的值就是(dep[y]-dep[x1]+1)*W1+(dep[y]-dep[x2]+1)*W2+(dep[y]-dep[x3]+1)*W3。

拆一下，变成(dep[y]+1)*(W1+W2+W3)  +  (-dep[x1]*W1-dep[x2]*W2-dep[x3]*W3)

前者的dep[y]+1是已知的，W1+W2+W3在修改时就加给了y，这时询问L[y]的值，再和dep[y]+1相乘就行了。

后者的三坨也都是在修改时就加给了y，询问L[y]的值即可。【用两个不同的树状数组维护的】

然后把两个值加起来就得到了y到根的距离。后面再链求和就不赘述了。

【没有代码，因为没有板子题】