算法与数据结构（Java解八皇后问题）

最新推荐文章于 2023-04-21 11:26:23 发布

Fu Junzhe

最新推荐文章于 2023-04-21 11:26:23 发布

阅读量227

点赞数

CC 4.0 BY-SA版权

分类专栏：算法与数据结构文章标签：数据结构算法

本文链接：https://blog.youkuaiyun.com/fujz123/article/details/105848147

算法与数据结构专栏收录该内容

25 篇文章

订阅专栏

本文详细解析了八皇后问题的解决思路，通过递归算法和冲突检测函数，实现了皇后在棋盘上的正确放置，展示了如何避免皇后之间的相互攻击。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

八皇后问题

思路：

八个皇后互不冲突，即同一行同一列只能出现一位皇后。以行为标准，每一行只能放入一位皇后。可以使用一个一维数组来表示皇后的位置，一维数组的下表表示行数，一维数组中的元素表示列数。

    int[] posQueen = new int[maxQueen];
    // posQueen = {0, 4, 7, 5, 2, 6, 1, 3} 表示在第一位皇后在第1行， 第1列；第二位皇后在第2行，第5列,以此类推...

当放入第n位皇后时，前面（n-1）行已经有皇后了，所以需要判断第 n 位皇后是否与前（n-1）位冲突。所以需要有一个检测冲突的函数：

    //检测第n个皇后是否和前面冲突
    	private boolean check(int n) {
    		 for (int i=0; i<n; i++) {
    			 if (posQueen[n] == posQueen[i] //在同一列
               ||Math.abs(n-i) == Math.abs(posQueen[n]-posQueen[i])) //在正、反对角线上
           { 
    				 return false;
    			 }
    		 }
    		 return true;
    	}

写好了检测冲突方法，就可以考虑开始放入皇后了，在这里用递归可以找出所有的可行解：

    //放置第n个皇后
    	private void place(int n) {
    		//检测是否所有皇后已放好
    		if (n==8) {
    			count++;
    			display();
    			return;
    		}
    		//依次放入皇后，并判断是否冲突
    		for(int i=0; i<maxQueen; i++) {
    			//先把当前皇后放在第1列
    			posQueen[n] = i;
    			//判断是否冲突
    			if (check(n)) {
    				//不冲突，进入下一层
    				place(n+1);
    			} 
    			//冲突，检查本行的下一个位置是否可行，即进入for循环的下一位
    		}
    	}

以5皇后举例说明：

这个方法需要输入当前第几个皇后正在被放置，在开始时我们会输入0（也就是放置第1位皇后）。

首先会检测5位皇后是否已经被放好，否，进行下一步，将第1位皇后放在第1行的第1列上，用{0,0,0,0,0}表示此时的状态；
然后判断是否冲突，否，进入下一层循环，放置第2位皇后；
先检测5位皇后是否都被放好，否，将第2位皇后放在第2行第1列上，冲突；
将第2位皇后右移一位，放在第2行第2列上，冲突；
将第2位皇后右移一位，放在第2行第3列上，不冲突，此时状态为{0,2,0,0,0}
进入下一层循环，放置第3位皇后；
先检测5位皇后是否都被放好，否，将第3位皇后放在第3行第1列上，冲突；
将第3位皇后右移一位，放在第3行第2列上，冲突；
…
将第3位皇后右移一位，放在第3行第5列上，不冲突，此时状态为{0,2,4,0,0}
进入下一层循环，放置第四位皇后；
同理，状态为{0,2,4,1,0}，进入下一层循环，放置第5位皇后；
同理，当for循环到i=4时，状态为{0,2,4,1,3}，第5位皇后不冲突，进入下一层循环；
因为5位皇后都已经被放置好，因此 if 检测为 true，输出第一组合理排列；
返回到上一层循环中，即回到第5步，并继续第5步（因为上一次第5步只检查到第5行第4列）；
直接从for循环的i=5开始，将第5位皇后放在第5行第5列上，冲突；
这一轮搜索结束，退回上一层，即第4步，从for循环的i=2开始，重复上述过程；
直到返回第1步，从for循环的i=1开始，重复第2-7步
最终会遍历所有位置，找出所有的组合方式

图解：

先从最后一行开始遍历；然后回到上一行，遍历；直到回到第一行

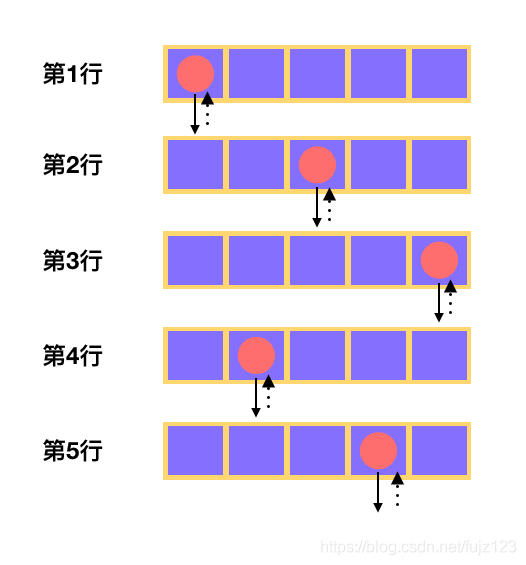
在这里插入图片描述

完整代码

public class Queen {

	//皇后的数量
	int maxQueen = 5;
	//皇后的位置数组，例：{0, 4, 7, 5, 2, 6, 1, 3}
	int[] posQueen = new int[maxQueen];
	//解法总数量
	int count = 0;
	
	//检测第n个皇后是否和前面冲突
	private boolean check(int n) {
		 for (int i=0; i<n; i++) {
			 if (posQueen[n] == posQueen[i] || Math.abs(n-i) == Math.abs(posQueen[n]-posQueen[i])) {
				 return false;
			 }
		 }
		 return true;
	} 
	
	//放置第n个皇后
	private void place(int n) {
		//检测是否所有皇后已放好
		if (n==maxQueen) {
			count++;
			display();
			return;
		}
		//依次放入皇后，并判断是否冲突, i表示当前皇后放置在第n+1行第i+1列
		for(int i=0; i<maxQueen; i++) {
			//先把当前皇后放在第1列
			posQueen[n] = i;
			//判断是否冲突
			if (check(n)) {
				//不冲突，进入下一层
				place(n+1);
			} 
			//冲突，检查本行的下一个位置是否可行，即进入for循环的下一位
		}
	} 
	
	//打印结果
	private void display() {
		System.out.println("第"+count+"种解法：");
		int[][] result = new int[posQueen.length][posQueen.length];
		for(int i=0; i<posQueen.length; i++) {
			result[i][posQueen[i]] = 1;
			for (int j=0; j<posQueen.length; j++) {
				System.out.print(result[i][j]+" ");
			}
			System.out.println();	
		}
	}
	
	
	public static void main(String[] args) {
		Queen queen = new Queen();
		queen.place(0);
		System.out.println(queen.maxQueen+"皇后问题一共有"+queen.count+"种解法。");
	}

}