理解和实现LRU缓存机制-优快云博客

背景

最近面了一个公司，有几道关于最近最少使用的选择题，由于没有明白LRU的含义，导致挂了。今天又看到了这道编程题，尝试自己做，做不出来。后来看了B站的一个视频，照着做了一下，做出来了。但花的时间远远超过了题目给定的时间。结论是，如果下次面试遇到同样的编程题，大概率还是挂。对于我这种反映慢的人，已经不适合这种面试了。工作中遇到同样的问题，大概率是可以解决的，无非时间比别人多花一点。但面试中遇到，没有提前学过或者练过，完全靠自己的设计能力做出来，只能膜拜这类人物了。

最后申明一下：下面的笔记来源于B站：就海海海波吧账号的视频内容。但视频内容里面的代码不全，我自己补全了，厚着脸皮把文章标记为原创了。如果有冒犯原作者的地方，留言我会删除。本来不想写博客记录的，只是B站的评论内容长度限制了我添加完整的代码。在此申明。

LRU

LRU 全称是 Least Recently Used, 即最近最久未使用的意思。

关键点

一个最大容量，两个API
保证都是O(1)的时间复杂度
上一次访问的元素排在队列的第一个

/*缓存容量为2*/
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头，右边是队尾
// 最近使用的排在队头，很久未使用的排在队尾
cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1);// 返回 1
// cache = [(1, 1), (2, 2)]
// 解释：因为最近访问了键1， 所以提前至队头
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释： 缓存容量已满，需要删除内容空出位置
// 优先删除久未使用的数据， 也就是队尾的数据
// 然后把新的数据插入队头
cache.get(2); // 返回 -1(未找到)
// cache = [(3, 3), (1, 1)]
// 解释： cache 中不存在键为 2 的数据
cache.put(1, 4);
// cache = [(1, 4), (3, 3)]
// 解释：键 1 已存在，把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头

特性：
查找快，插入快
删除快，有顺序之分

Map? 不是有序的呀。

双向链表+散列表。

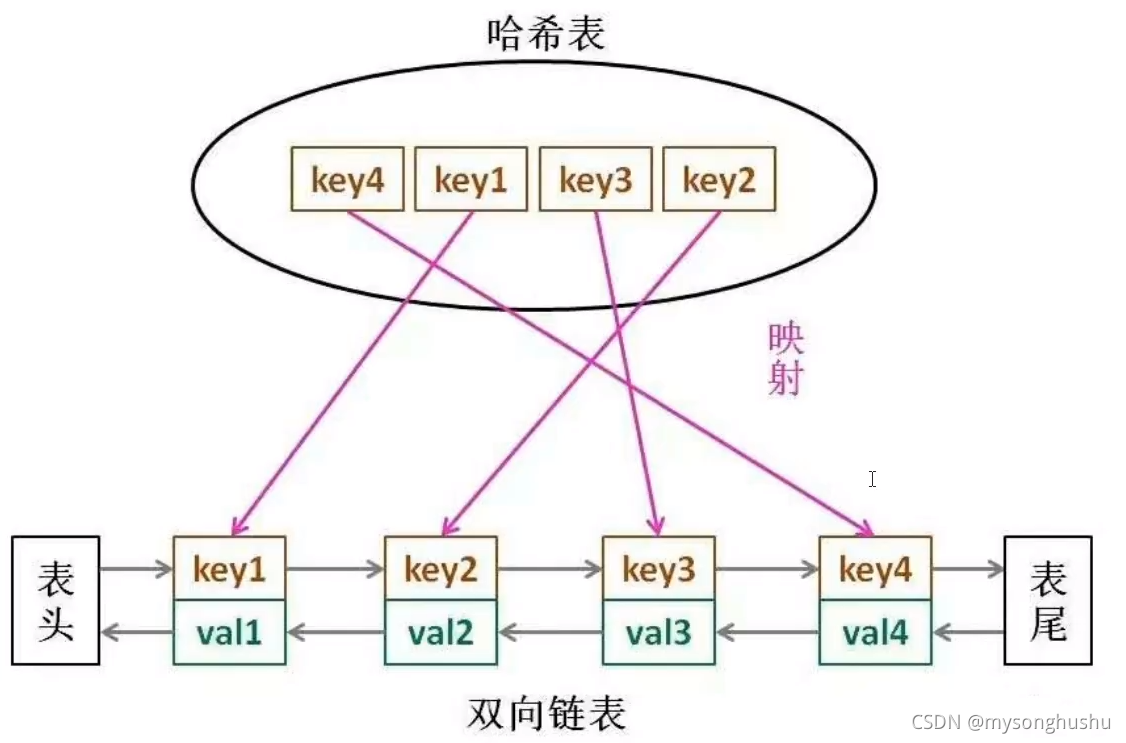
hash表加双向链表

代码实现

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;

public class Solution {
//    public static void main(String[] args) {
//        Solution solution = new Solution();
//
//        // [[1,1,1],[1,1,2],[2,1]],3
//        int[][] operators = new int[3][];
//        operators[0] = new int[] {1, 1, 1};
//        operators[1] = new int[] {1, 1, 2};
//        operators[2] = new int[] {2, 1};
//
////        int[][] operators = new int[6][];
////        operators[0] = new int[] {1, 1, 1};
////        operators[1] = new int[] {1, 2, 2};
////        operators[2] = new int[] {1, 3, 2};
////        operators[3] = new int[] {2, 1};
////        operators[4] = new int[] {1, 4, 4};
////        operators[5] = new int[] {2, 2};
//
//        int k = 3;
//        int[] result = solution.LRU(operators, k);
//        System.out.println(Arrays.toString(result));
//
//    }
    /**
     * lru design
     * @param operators int整型二维数组 the ops
     * @param k int整型 the k
     * @return int整型一维数组
     */
    public int[] LRU (int[][] operators, int k) {
        // write code here
        LRUCache lruCache = new LRUCache(k);
        ArrayList<Integer> output = new ArrayList();
        for(int i=0; i<operators.length; i++) {
            int[] operator = operators[i];
            int operateCode = operator[0];
            int operateKey = operator[1];
            // 添加
            if (operateCode == 1) {
               lruCache.put(operateKey, operator[2]);
            } else if (operateCode == 2) { //查询
                int res = lruCache.get(operateKey);
                output.add(res);
            }
        }
        int[] out = new int[output.size()];
        for (int i=0; i<output.size(); i++) {
           out[i] =output.get(i);
        }
        return out;
    }

    class LRUCache {
        private int capacity;
        DoubleList list;
        HashMap<Integer, Node> map;

        public LRUCache(int cap) {
            this.capacity = cap;
            list = new DoubleList();
            map = new HashMap<>();
        }

        /**
         * 没有
         * 有
         * @param key
         * @return
         */
        public int get(int key) {
            if (!map.containsKey(key)) {
                return -1;
            }
            // 先得到对应的value.
            int res = map.get(key).value;
            // 将对应的节点提到队列的头部
            put(key, res);
            return res;
        }

        public void put(int key, int val) {
            Node node = new Node(key, val);
            if (map.containsKey(key)) {
                list.remove(map.get(key));
                list.addFirst(node);
                map.put(key, node);
            } else {
                if (capacity == list.size()) {
                    Node last = list.removeLast();
                    map.remove(last.key);
                }
                list.addFirst(node);
                map.put(key, node);
            }
        }
    }

    class Node {
        public int key;
        public int value;
        public Node next;
        public Node prev;

        public Node(int k, int v) {
            this.key = k;
            this.value = v;
        }
    }

    class DoubleList {
        Node head;
        Node tail;
        int size;

        public void addFirst(Node node) {
            if (null == head && null == tail) {
                head = node;
                tail = node;
                size = 1;
                return;
            }
            node.next = head;
            head.prev = node;
            head = node;
            size = size+1;
        }

        public void remove(Node node) {
            if (node == null) {
                return;
            }
            // 1 <-> 2 <-> 3
            Node previous = node.prev;
            Node next = node.next;
            // 移除头结点
            if (null == previous) {
                head = node.next;
                node.next = null;
                if (head != null) {
                    head.prev = null;
                } else {
                    tail = null;
                }
            } else if (null == next) { // 移除尾结点
                tail = node.prev;
                tail.next = null;
                node.prev = null;
            } else {
                previous.next = next;
                next.prev = previous;
            }
            size = size - 1;
        }

        public Node removeLast() {
            Node res = tail;
            Node tailPrev = tail.prev;
            tailPrev.next = null;
            tail.prev = null;
            tail = tailPrev;
            size = size - 1;
            return res;
        }

        public int size() {
            return size;
        }
    }
}
···