用过哪些Map类,都有什么区别,HashMap是线程安全的吗,并发下使用的Map是什么,他们内部原理分别是什么,比如存储方式,hashcode,扩容,默认容量等。
先上图
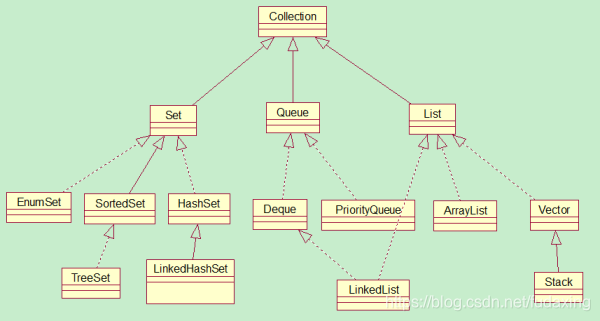
Set和List接口是Collection接口的子接口,分别代表无序集合和有序集合,Queue是Java提供的队列实现。
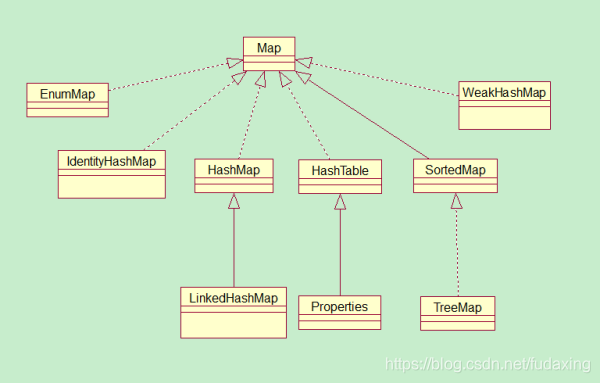
Map用于保存具有key-value映射关系的数据
Java 中有四种常见的Map实现——HashMap, TreeMap, Hashtable和LinkedHashMap:
- HashMap就是一张hash表,键和值都没有排序。
- TreeMap以红黑树结构为基础,键值可以设置按某种顺序排列。
- LinkedHashMap保存了插入时的顺序。
- Hashtable是同步的(而HashMap是不同步的)。所以如果在线程安全的环境下应该多使用HashMap,而不是Hashtable,因为Hashtable对同步有额外的开销,不过JDK 5之后的版本可以使用conncurrentHashMap代替HashTable。
本文重点总结HashMap,HashMap是基于哈希表实现的,每一个元素是一个key-value对,其内部通过单链表解决冲突问题,容量不足(超过了阀值)时,同样会自动增长。
HashMap是非线程安全的,只用于单线程环境下,多线程环境下可以采用concurrent并发包下concurrentHashMap。
HashMap 实现了Serializable接口,因此它支持序列化。
HashMap还实现了Cloneable接口,故能被克隆。
关于hashmap的用法,这里就不再赘述了,只说原理和一些注意点。
- HashMap的存储结构
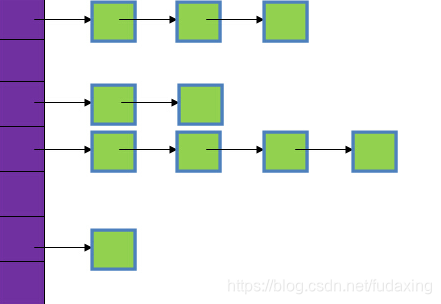
紫色部分即代表哈希表本身(其实是一个数组),数组的每个元素都是一个单链表的头节点,链表是用来解决hash地址冲突的,如果不同的key映射到了数组的同一位置处,就将其放入单链表中保存。
HashMap有四个构造方法,方法中有两个很重要的参数:初始容量 和 加载因子
/**
* Constructs an empty <tt>HashMap</tt> with the specified initial
* capacity and load factor.
*
* @param initialCapacity the initial capacity
* @param loadFactor the load factor
* @throws IllegalArgumentException if the initial capacity is negative
* or the load factor is nonpositive
*/
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
这两个参数是影响HashMap性能的重要参数,其中容量表示哈希表中槽的数量(即哈希数组的长度),初始容量是创建哈希表时的容量(默认为16),加载因子是哈希表当前key的数量和容量的比值,当哈希表中的条目数超出了加载因子与当前容量的乘积时,则要对该哈希表提前进行 resize 操作(即扩容)。
- 如果加载因子越大,对空间的利用更充分,但是查找效率会降低(链表长度会越来越长);
- 如果加载因子太小,那么表中的数据将过于稀疏(很多空间还没用,就开始扩容了),严重浪费。
JDK开发者规定的默认加载因子为0.75,因为这是一个比较理想的值。另外,无论指定初始容量为多少,构造方法都会将实际容量设为不小于指定容量的2的幂次方,且最大值不能超过2的30次方。
重点分析HashMap中用的最多的两个方法put和get的源码
- get方法源码
// 获取key对应的value
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
/**
* Implements Map.get and related methods
*
* @param hash hash for key
* @param key the key
* @return the node, or null if none
*/
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
- TreeNode源码
/* ------------------------------------------------------------ */
// Tree bins
/**
* Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn
* extends Node) so can be used as extension of either regular or
* linked node.
*/
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
/**
* Returns root of tree containing this node.
*/
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
/**
* Ensures that the given root is the first node of its bin.
*/
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
if (root != first) {
Node<K,V> rn;
tab[index] = root;
TreeNode<K,V> rp = root.prev;
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
if (first != null)
first.prev = root;
root.next = first;
root.prev = null;
}
assert checkInvariants(root);
}
}
/**
* Finds the node starting at root p with the given hash and key.
* The kc argument caches comparableClassFor(key) upon first use
* comparing keys.
*/
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}
/**
* Calls find for root node.
*/
final TreeNode<K,V> getTreeNode(int h, Object k) {
return ((parent != null) ? root() : this).find(h, k, null);
}
/**
* Tie-breaking utility for ordering insertions when equal
* hashCodes and non-comparable. We don't require a total
* order, just a consistent insertion rule to maintain
* equivalence across rebalancings. Tie-breaking further than
* necessary simplifies testing a bit.
*/
static int tieBreakOrder(Object a, Object b) {
int d;
if (a == null || b == null ||
(d = a.getClass().getName().
compareTo(b.getClass().getName())) == 0)
d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
-1 : 1);
return d;
}
/**
* Forms tree of the nodes linked from this node.
* @return root of tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}
/**
* Returns a list of non-TreeNodes replacing those linked from
* this node.
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
/**
* Tree version of putVal.
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
/**
* Removes the given node, that must be present before this call.
* This is messier than typical red-black deletion code because we
* cannot swap the contents of an interior node with a leaf
* successor that is pinned by "next" pointers that are accessible
* independently during traversal. So instead we swap the tree
* linkages. If the current tree appears to have too few nodes,
* the bin is converted back to a plain bin. (The test triggers
* somewhere between 2 and 6 nodes, depending on tree structure).
*/
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // detach
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
/**
* Splits nodes in a tree bin into lower and upper tree bins,
* or untreeifies if now too small. Called only from resize;
* see above discussion about split bits and indices.
*
* @param map the map
* @param tab the table for recording bin heads
* @param index the index of the table being split
* @param bit the bit of hash to split on
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
/* ------------------------------------------------------------ */
// Red-black tree methods, all adapted from CLR
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
return root;
if (xp == (xppl = xpp.left)) {
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
/**
* Recursive invariant check
*/
static <K,V> boolean checkInvariants(TreeNode<K,V> t) {
TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right,
tb = t.prev, tn = (TreeNode<K,V>)t.next;
if (tb != null && tb.next != t)
return false;
if (tn != null && tn.prev != t)
return false;
if (tp != null && t != tp.left && t != tp.right)
return false;
if (tl != null && (tl.parent != t || tl.hash > t.hash))
return false;
if (tr != null && (tr.parent != t || tr.hash < t.hash))
return false;
if (t.red && tl != null && tl.red && tr != null && tr.red)
return false;
if (tl != null && !checkInvariants(tl))
return false;
if (tr != null && !checkInvariants(tr))
return false;
return true;
}
}
```
put方法源码
```java
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
注意这里倒数第三行的构造方法,将key-value键值对赋给table[bucketIndex],并将其next指向元素e,这便将key-value放到了头结点中,并将之前的头结点接在了它的后面。该方法也说明,每次put键值对的时候,总是将新的该键值对放在table[bucketIndex]处(即头结点处)。两外注意最后两行代码,每次加入键值对时,都要判断当前已用的槽的数目是否大于等于阀值(容量*加载因子),如果大于等于,则进行扩容,将容量扩为原来容量的2倍。
重点来分析下求hash值和索引值的方法,这两个方法便是HashMap设计的最为核心的部分,二者结合能保证哈希表中的元素尽可能均匀地散列。
由hash值找到对应索引的方法如下
static int indexFor(int h, int length) {
return h & (length-1);
}
因为容量初始还是设定都会转化为2的幂次。故可以使用高效的位与运算替代模运算。下面会解释原因。
下面是几个常见的面试题
说下hashmap的 扩容机制?
前面说了,hashmap的构造器里指明了两个对于理解HashMap比较重要的两个参数 int initialCapacity, float loadFactor,这两个参数会影响HashMap效率,HashMap底层采用的散列数组实现,利用initialCapacity这个参数我们可以设置这个数组的大小,也就是散列桶的数量,但是如果需要Map的数据过多,在不断的add之后,这些桶可能都会被占满,这是有两种策略,一种是不改变Capacity,因为即使桶占满了,我们还是可以利用每个桶附带的链表增加元素。但是这有个缺点,此时HaspMap就退化成为了LinkedList,使get和put方法的时间开销上升,这是就要采用另一种方法:增加Hash桶的数量,这样get和put的时间开销又回退到近于常数复杂度上。Hashmap就是采用的该方法。
关于扩容。看hashmap的扩容方法,resize方法,它的源码如下
扩容的resize方法
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
很明显,扩容是一个相当耗时的操作,因为它需要重新计算这些元素在新的数组中的位置并进行复制处理。因此,我们在用HashMap时,最好能提前预估下HashMap中元素的个数,这样有助于提高HashMap的性能。
hashmap什么时候需要增加容量呢?
因为效率问题,JDK采用预处理法,这时前面说的loadFactor就派上了用场,当size > initialCapacity * loadFactor,hashmap内部resize方法就被调用,使得重新扩充hash桶的数量,在目前的实现中,是增加一倍,这样就保证当你真正想put新的元素时效率不会明显下降。所以一般情况下HashMap并不存在键值放满的情况。当然并不排除极端情况,比如设置的JVM内存用完了,或者这个HashMap的Capacity已经达到了MAXIMUM_CAPACITY(目前的实现是2^30)。
initialCapacity和loadFactor参数设什么样的值好呢?
initialCapacity的默认值是16,有些人可能会想如果内存足够,是不是可以将initialCapacity设大一些,即使用不了这么大,就可避免扩容导致的效率的下降,反正无论initialCapacity大小,我们使用的get和put方法都是常数复杂度的。这么说没什么不对,但是可能会忽略一点,实际的程序可能不仅仅使用get和put方法,也有可能使用迭代器,如initialCapacity容量较大,那么会使迭代器效率降低。所以理想的情况还是在使用HashMap前估计一下数据量。
加载因子默认值是0.75,是JDK权衡时间和空间效率之后得到的一个相对优良的数值。如果这个值过大,虽然空间利用率是高了,但是对于HashMap中的一些方法的效率就下降了,包括get和put方法,会导致每个hash桶所附加的链表增长,影响存取效率。如果比较小,除了导致空间利用率较低外没有什么坏处,只要有的是内存,毕竟现在大多数人把时间看的比空间重要。但是实际中还是很少有人会将这个值设置的低于0.5。
HashMap的key和value都能为null么?如果k能为null,那么它是怎么样查找值的?
如果key为null,则直接从哈希表的第一个位置table[0]对应的链表上查找。记住,key为null的键值对永远都放在以table[0]为头结点的链表中。
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
HashMap中put值的时候如果发生了冲突,是怎么处理的?
JDK使用了链地址法,hash表的每个元素又分别链接着一个单链表,元素为头结点,如果不同的key映射到了相同的下标,那么就使用头插法,插入到该元素对应的链表。
HashMap的key是如何散列到hash表的?相比较HashTable有什么改进?
我们一般对哈希表的散列很自然地会想到用hash值对length取模(即除留余数法),HashTable就是这样实现的,这种方法基本能保证元素在哈希表中散列的比较均匀,但取模会用到除法运算,效率很低,且hashtable直接使用了hashcode值,没有重新计算。
HashMap中则通过 hash&(length-1) 的方法来代替取模,其中h是key的hash值,同样实现了均匀的散列,但效率要高很多,这也是HashMap对Hashtable的一个改进。
接下来,我们分析下为什么哈希表的容量一定要是2的整数次幂。
首先,length为2的整数次幂的话,h&(length-1) 在数学上就相当于对length取模,这样便保证了散列的均匀,同时也提升了效率;
其次,length为2的整数次幂的话,则一定为偶数,那么 length-1 一定为奇数,奇数的二进制的最后一位是1,这样便保证了 h&(length-1) 的最后一位可能为0,也可能为1(这取决于h的值),即与后的结果可能为偶数,也可能为奇数,这样便可以保证散列的均匀,而如果length为奇数的话,很明显 length-1 为偶数,它的最后一位是0,这样 h&(length-1) 的最后一位肯定为0,即只能为偶数,这样导致了任何hash值都只会被散列到数组的偶数下标位置上,浪费了一半的空间,因此length取2的整数次幂,是为了使不同hash值发生碰撞的概率较小,这样就能使元素在哈希表中均匀地散列。
作为对比,在讨论一下Hashtable
HashTable同样是基于哈希表实现的,其实类似HashMap,只不过有些区别,HashTable同样每个元素是一个key-value对,其内部也是通过单链表解决冲突问题,容量不足(超过了阀值)时,同样会自动增长。
HashTable比较古老, 是JDK1.0就引入的类,而HashMap 是 1.2 引进的 Map 的一个实现。
HashTable 是线程安全的,能用于多线程环境中。Hashtable同样也实现了Serializable接口,支持序列化,也实现了Cloneable接口,能被克隆。
Hashtable继承于Dictionary类,实现了Map接口。Dictionary 是声明了操作"键值对"函数接口的抽象类。 有一点注意,HashTable除了线程安全之外(其实是直接在方法上增加了synchronized关键字,比较古老,落后,低效的同步方式),还有就是它的key、value都不为null。另外Hashtable 也有 初始容量 和 加载因子。
/**
* Constructs a new, empty hashtable with a default initial capacity (11)
* and load factor (0.75).
*/
public Hashtable() {
this(11, 0.75f);
}
默认加载因子也是 0.75,HashTable在不指定容量的情况下的默认容量为11,而HashMap为16,Hashtable不要求底层数组的容量一定要为2的整数次幂,而HashMap则要求一定为2的整数次幂。因为HashTable是直接使用除留余数法定位地址。且Hashtable计算hash值,直接用key的hashCode()。
还要注意:前面说了Hashtable中key和value都不允许为null,而HashMap中key和value都允许为null(key只能有一个为null,而value则可以有多个为null)。但如在Hashtable中有类似put(null,null)的操作,编译同样可以通过,因为key和value都是Object类型,但运行时会抛出NullPointerException异常,这是JDK的规范规定的。
最后针对扩容:Hashtable扩容时,将容量变为原来的2倍加1,而HashMap扩容时,将容量变为原来的2倍。
下面是几个常见的笔试,面试题
- HashTable和HashMap的区别有哪些?
HashMap和Hashtable都实现了Map接口,但决定用哪一个之前先要弄清楚它们之间的分别。主要的区别有:线程安全性,同步(synchronization),以及速度。
理解HashMap是Hashtable的轻量级实现(非线程安全的实现,hashtable是非轻量级,线程安全的),都实现Map接口,主要区别在于:- 1、由于HashMap非线程安全,在只有一个线程访问的情况下,效率要高于HashTable
- 2、HashMap允许将null作为一个entry的key或者value,而Hashtable不允许。
- 3、HashMap把Hashtable的contains方法去掉了,改成containsValue和containsKey。因为contains方法容易让人引起误解。
- 4、Hashtable继承自陈旧的Dictionary类,而HashMap是Java1.2引进的Map 的一个实现。
- 5、Hashtable和HashMap扩容的方法不一样,HashTable中hash数组默认大小11,扩容方式是 old*2+1。HashMap中hash数组的默认大小是16,而且一定是2的指数,增加为原来的2倍,没有加1。
- 6、两者通过hash值散列到hash表的算法不一样,HashTbale是古老的除留余数法,直接使用hashcode,而HashMap是强制容量为2的幂,重新根据hashcode计算hash值,在使用hash 位与 (hash表长度 – 1),也等价取膜,但更加高效,取得的位置更加分散,偶数,奇数保证了都会分散到。前者就不能保证。
- 7、另一个区别是HashMap的迭代器(Iterator)是fail-fast迭代器,而Hashtable的enumerator迭代器不是fail-fast的。所以当有其它线程改变了HashMap的结构(增加或者移除元素),将会抛 ConcurrentModificationException,但迭代器本身的remove()方法移除元素则不会抛出ConcurrentModificationException异常。但这并不是一个一定发生的行为,要看JVM。这条同样也是Enumeration和Iterator的区别。
fail-fast和iterator迭代器相关。如果某个集合对象创建了Iterator或者ListIterator,然后其它的线程试图“结构上”更改集合对象,将会抛出ConcurrentModificationException异常。但其它线程可以通过set()方法更改集合对象是允许的,因为这并没有从“结构上”更改集合。但是假如已经从结构上进行了更改,再调用set()方法,将会抛出IllegalArgumentException异常。
结构上的更改指的是删除或者插入一个元素,这样会影响到map的结构。
该条说白了就是在使用迭代器的过程中有其他线程在结构上修改了map,那么将抛出ConcurrentModificationException,这就是所谓fail-fast策略。
- 为什么HashMap是线程不安全的,实际会如何体现?
- 第一,如果多个线程同时使用put方法添加元素
假设正好存在两个put的key发生了碰撞(hash值一样),那么根据HashMap的实现,这两个key会添加到数组的同一个位置,这样最终就会发生其中一个线程的put的数据被覆盖。 - 第二,如果多个线程同时检测到元素个数超过数组大小*loadFactor
这样会发生多个线程同时对hash数组进行扩容,都在重新计算元素位置以及复制数据,但是最终只有一个线程扩容后的数组会赋给table,也就是说其他线程的都会丢失,并且各自线程put的数据也丢失。且会引起死循环的错误。
- 第一,如果多个线程同时使用put方法添加元素
具体细节上的原因,可以参考:不正当使用HashMap导致cpu 100%的问题追究
- 能否让HashMap实现线程安全,如何做?
- 1、直接使用Hashtable,但是当一个线程访问HashTable的同步方法时,其他线程如果也要访问同步方法,会被阻塞住。举个例子,当一个线程使用put方法时,另一个线程不但不可以使用put方法,连get方法都不可以,效率很低,现在基本不会选择它了。
- 2、HashMap可以通过下面的语句进行同步:
Collections.synchronizeMap(hashMap);- 3、直接使用JDK 5 之后的 ConcurrentHashMap,如果使用Java 5或以上的话,请使用ConcurrentHashMap。
JAVA8的ConcurrentHashMap为什么放弃了分段锁,有什么问题吗,如果你来设计,你如何设计。
先看看ConcurrentHashMap的说法吧:
一个哈希表,支持检索的完全并发和更新的高预期并发性。该类遵循与java.util.Hashtable相同的功能规范,并包括与Hashtable的每个方法对应的方法版本。但是,即使所有操作都是线程安全的,检索操作也不需要锁定,并且不支持以阻止所有访问的方式锁定整个表。在依赖于线程安全但不依赖于其同步细节的程序中,此类可与Hashtable完全互操作。
检索操作{@code get}通常不会阻塞,因此可能与更新操作{@code put}和{@code remove}重叠。检索反映了最近完成的更新操作的结果。 (更正式地说,给定密钥的更新操作承担与该密钥报告更新值的任何(非空)检索之前发生的关系。)对于诸如{@code putAll}和{@code clear}之类的聚合操作,并发检索可能反映只插入或删除一些条目。类似地,Iterators,Spliterators和Enumerations在迭代器/枚举的创建时或之后的某个时刻返回反映哈希表状态的元素。它们不会抛出java.util.ConcurrentModificationException ConcurrentModificationException。但是,迭代器设计为一次只能由一个线程使用。请记住,包括{@code size},{@ code isEmpty}和{@code containsValue}在内的聚合状态方法的结果通常仅在 Map 未在其他线程中进行并发更新时才有用。否则,这些方法的结果反映了可能足以用于监视或估计目的的瞬态,但不适用于程序控制。
当存在太多冲突时(即,具有不同哈希码的密钥但落入与表大小模数相同的槽中的密钥),该表被动态扩展,具有每个映射大致保持两个箱的预期平均效果(对应于0.75负载)调整大小的因子阈值)。随着映射的添加和删除,这个平均值可能会有很大的差异,但总的来说,这维持了哈希表的普遍接受的时间/空间权衡。但是,调整此大小或任何其他类型的散列表可能是一个相对较慢的操作。在可能的情况下,最好将大小估计值作为可选的{@code initialCapacity}构造函数参数提供。另一个可选的{@code loadFactor}构造函数参数通过指定在计算给定数量的元素时要分配的空间量时使用的表密度,提供了另一种自定义初始表容量的方法。此外,为了与此类的先前版本兼容,构造函数可以选择指定预期的{@code concurrencyLevel}作为内部大小调整的附加提示。请注意,使用具有完全相同的{@code hashCode()}的许多键是降低任何哈希表性能的可靠方法。为了改善影响,当密钥为{@link Comparable}时,此类可以使用密钥之间的比较顺序来帮助打破关系。





















 16万+
16万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








