读书笔记《Outlier Analysis》 第四章 基于邻近的异常检测

1.基本介绍

基于邻近的技术是指，当一个数据点的位置或邻近是稀疏时，则将其定义为一个离群点。

1.1 基于邻近的技术最常见的三种离群点分析的定义：

基于聚类：

使用非任何聚类中数据点的成员、其与其他聚类质心的距离、最近的聚类的大小或这些因素的组合来量化异常值评分。聚类问题和异常检测问题有互补关系，其中要么属于聚类，要么属于异常值。

基于距离：

使用数据点到其k近邻的距离来定义邻近。具有较大k近邻距离的数据点被定义为离群点。基于距离的算法通常比其他两种方法需要执行更详细的粒度。另一方面，这种更大的粒度往往需要很大的计算成本（因为其需要计算每个数据点到其k邻近的数据点的距离）。

基于密度：

数据点的指定局部区域（网格区域或基于距离的区域）内的其他点的数量，用于定义局部密度。这些局部密度值可以转换为异常值分数。也可以使用其他基于核的方法或用于密度估计的统计方法。聚类和基于密度的方法的主要区别在于，基于聚类的方法是划分数据点，而基于密度的方法是划分数据空间。

1.2 各种邻近方法的比较：主要是执行分析的粒度级别不同

显然，所有这些技术都是密切相关的，因为他们是基于某种邻近（或相似）的概念。主要区别在于如何定义这种邻近的详细程度。

基于距离的方法和其他两种方法的一个主要区别在于执行分析的粒度级别。

在基于聚类和密度的方法中，数据在异常分析之前通过划分【数据点或数据空间】进行预聚集。将数据点与此预聚集数据中的分布进行比较以进行分析。

另一方面，在基于距离的方法中，K近邻到原始数据点的距离被计算为异常值分数。

因此，最近邻方法（基于距离）中的分析是在比聚类方法更详细的粒度级别上进行的。

最近邻方法计算距离时，可以使用索引和剪枝技术来加快计算速度（索引和剪枝技术只在一些受限的数据集（如低维数据集）中有效），否则需要O(N2)时间来计算（具有N个记录）。此外，剪枝不是为异常值分数计算而设计的，他只能用于需要报告二进制标签（指示是否为异常点）的设置。

1.3 邻近方法的适用性：

最近邻方法特别适用于对于不可能进行稳健聚类或密度分析的较小数据集。

基于邻近的方法适合用来检测噪声和异常值。

基于邻近的方法的可解释性较好，也适合各种数据类型，如时间序列数据、图形数据、序列数据等。

 

2.基于聚类的方法

简单理解就是基于聚类的方法和异常值时互补关系的，即一个数据点要么属于任何一个簇，要么不属于任何要给簇。不属于任何一个簇的数据点即为异常值。

在聚类中，目标是将点划分为密集的子集，而在异常检测中，目标是识别不属于任何一个密集子集的数据点。

2.1 异常值的定义

问题：不属于任何簇的数据点不一定是异常值，也有可能是弱离群点或噪声；非常小的簇也有可能被视为异常值。简单使用欧式距离来计算异常值分数可能不适合。

解决方法：

由于簇可能有不同的形状和方向，因此，可以使用马氏距离来计算数据点到簇质心的距离来构造异常值分数。可以将马氏距离看作是经过一些变换和缩放后的点与簇质心之间的调整的欧式距离。具体来说就是点和质心被转换为由主成分方向定义的轴系。

案例：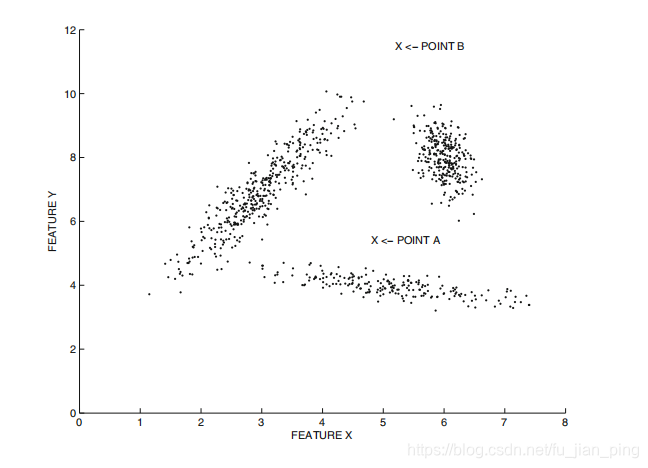

 从上图所示的示例中可以明显看出这一点，其中数据点‘A’比数据点‘B’更明显地是一个离群点，因为后者可能与拉长的簇之一有关。 然而，这种微妙的区别不能用欧氏距离来检测，根据欧氏距离，数据点‘A’最接近最近的聚类质心。

一个结论：聚类过程对底层数据集群的不同形状和方向比较敏感。

（书中还提到除了距离的标准外，还可以将集群基数作为异常值分数的组成部分。基数准则在基于直方图的方法中特别流行，其中空间被划分为大小大致相等的区域。 值得注意的是，基于直方图的方法是聚类方法的变体。 将聚类基数纳入分数有助于区分小群聚类离群点和大群聚类中的正常点。）

2.2 集体异常

一个识别集体（小的簇）异常的方法：可以通过设定一个阈值，如果簇的数据点数量少于这个阈值，才定义为异常值。

2.3 预测的变异性问题

基于聚类的方法的预测的变异性的原因：模型的选择、初始化、参数的设置（如k，簇的数量）。

为了提高性能，可以使用集成学习的思想，即通常最好使用来自多个集群（具有不同参数设置）的离群点分数的平均值来获得更好的结果。

一般来说，充分随机化往往比基本聚类方法的质量更重要。 在这方面，一个特别有用的方法是使用极其随机的森林聚类。

2.4 聚类类型的敏感

聚类集合的一个有趣特性是发现的离群点类型对所使用的聚类类型敏感。 例如，子空间聚类将产生子空间离群点(cf。 第5章第5.2.4节)；相关敏感聚类将产生相关敏感异常值，局部敏感聚类将产生局部敏感异常值。 通过组合不同的基聚类方法，可以发现不同类型的异常值。

2.5 任意聚类形状的扩展

前面提到的关于使用马氏距离计算数据点到质心的距离的方法对于椭圆形状的团簇比较有效，但是对于某些形状的数据集也许并不有效。如下图案例所示。

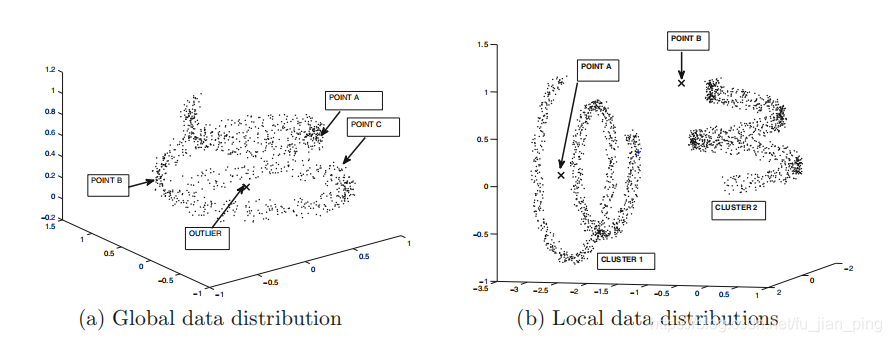
图（a）是一种全局流形的、单一的团簇。图（b）中左边簇1中的点A比许多其他点更接近簇1的质心。

解决方法：

对于图(a)的情况，只要使用非线性主成分（或核主成分）分析等方法将点映射到一个可以有效使用欧氏距离的新空间就足够了。

对于图(b)的情况，显然，我们需要某种类型的数据转换，它可以将点映射到一个新的空间，在这个空间中暴露出这些异常值。如对非线性主成分分析等方法进一步修改（这些修改来源于谱聚类spectral clustering的概念，是相似矩阵稀疏化sparsifification和局部归一化loc