深度学习复习笔记（7）分类任务——卷积

全连接：

回归与分类：

输出：

1、值离谁近就是哪一类。×不能用这种方式表示类别，因为所有类别都是等价的。如果按值的远近表示类，就引申了一个含义，A比起猫来说更像狗。

2、用独热编码表示类别。√

所有输入的图片必须相同的size。一般统一变成224*224

和回归不一样，求两个分布之间的loss，用交叉熵Cross entropy。

输入：

图片天生是三通道矩阵。

1、把矩阵拉直成向量，拼在一起。 

        

        参数量太多，非常容易过拟合。

        

2、卷积神经网络√

卷：拿着图一格一格挪动去比较。

积：格子分别各自相乘，再求和。

          卷积核⬆                             特征图⬆                         特征图⬆   

卷积核单次和特征图比对得到一个值（27个值得到1个值）

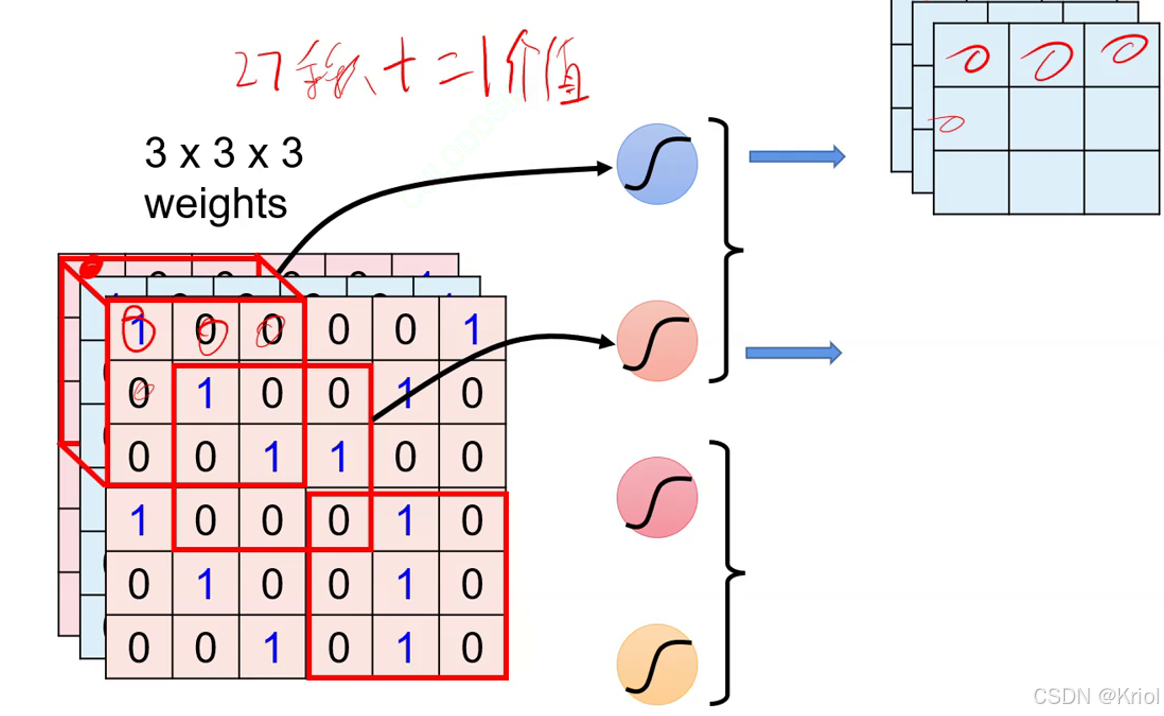
卷积核的大小称为神经元的感受野，即卷积核能看多大。（鸟嘴，鸟）

为了保持特征图大小不变，进行的操作：

1、补零。

特征图有多深，卷积核就得有多深。

一层卷积：下图红圈是一层卷积。五张图叠起来，再加上3*3*5的卷积核又是一层卷积。

特征图的厚度是靠卷积核的数量改变的，特征图的长宽是靠卷积核大小改变的。

参数：卷积核是模型的参数，上图第一层卷积的参数量是3*3*3*5（忽略bias）.

每次卷积参数量太大，运算量太多，所以要降采样方法（常用两种）：

1、扩大步长（少用）会丢失信息且引入复杂计算        2、池化pooling（常用）

卷积核计算公式：不能整除向下取整：

池化：用一个数表示多个数。

最大池化和平均池化：（常用最大池化，平均池化计算量大）而且一般只看最显著的特征。

pooling（2）表示2*2池化成1

适应性池化：Adaptive XXX Pool（7）表示无论多大，后面都变成7*7

一般情况希望通道数增加，特征图减少。通道数增大一倍，特征图缩小为原来1/4

卷一次池化一次：

等卷积和池化后，拉直数据，再全连接，得到数据判断类别：

输出的结果不是概率，所以要用softmax（）把输出转换为概率。y‘可称为概率分布。（将softmax的输出视作模型预测的概率分布。

对于概率分布，计算损失使用交叉熵。

对于二分类：

当y尖=1，那么后半部分为0，要想让Loss最小，希望y‘趋近于1，即y’和y尖接近，是一个类别。

当y尖=0，那么前半部分为0，要想让Loss最小，希望1-y‘趋近于1，y’趋近于0，即y‘和y不是一个类别。

对于多分类：样本真实标签*对应样本预测概率值 的 和 再除以样本数的负数

当y尖=1，那么希望loss越小越好，即pic越大越好。

交叉熵Loss的输入：

分类神经网络：

前向过程：

输入，卷积，池化，卷积，池化 循环，卷到一定程度 拉直，全连接，每个类别都得到一个值，值最大的就是模型预测出的类别。（把全连接后的值经过Softmax转化成概率，计算loss交叉熵）

反向过程：

通过backward（）梯度回传，得到每一个卷积核的每一个权重的梯度，通过优化器更新模型。

训练模型需要百万以上的带标签的图片才能有较好的训练效果，所以我们需要用到一些经典数据集。