迪杰斯特拉算法(Dijkstra)——最短路由算法

迪杰斯特拉算法(Dijkstra)——最短路由算法

---

---

1、问题介绍

如图所示：

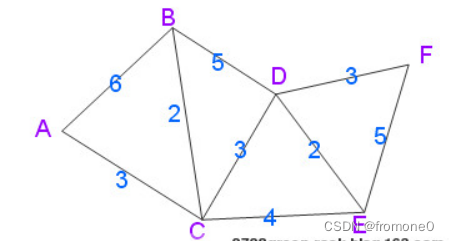
以A点为例，最短路由算法为：从A点出发到达其他各点所经过的边的权值相加最小的一条路径，称为最短路径。

主要算法：

1. 迪杰斯特拉算法（Dijkstra算法）
2. 弗洛伊德算法（Floyd算法）

2、算法思想

设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源顶点（A点）到该顶点的最短路径长度已知。初始时，S中仅含有源顶点。设u是图G的某一个顶点，把从源顶点到u且中间只经过S中顶点的路称为从源顶点到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

3、算法演示

以上图为例，演示从A点到各个顶点的最短距离。

第一步：声明 dist 数组，并设置初始值（为A到能直接到各点的距离）

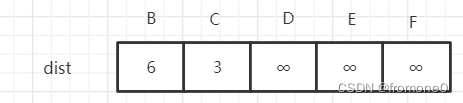
初始化顶点集S={1}

第二步：由于A能到各点的距离为dist数组中的数据，挑出dist中最小的距离，将该点放入顶点集S中，既：A点到C点的最小距离为3，其他点暂时没有放到顶点集S中，所以A点到其他各点的最短距离可能为dist数组中的数据，但是还不能准确的确定。

此时：S={1,3}、dist不变

第三步：既然我们现在确定了一个顶点的最短路径，那么我们从A点出发经过C点再去其他的点，这时A到各点的距离会不会发生改变，也就是在边<A,B>=6，而<A,C>+<C,B>=5，这个时候由于我们从A直接到B的权值为6，但是如果经过C再去B的总权值为5，所以目前从A到B的最短权值为5，但是现在还不能确定就是5，我们需要将经过C点到所有点的距离做一个临时数组，dist_temp：该数组存放C点到各点的最短路径。

将dist_temp中对应点与dist中的数据相加，如果结果小于dist中的数据就替换，不小于就不动（A经过C点到目标点的距离是否小于A直接到目标点的距离）
dist为

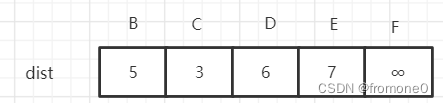
此时最小值为C，但是C点已经在集合S中，所以在找到下一个小的距离为B，B点没有在集合S中，此时将B放入S，则A到B的最短距离为5.

此时S={A,C,B}

…

以此类推，最终结果为：

迭代	S	B点	C点	D点	E点	F点
初始化	{A}	6	3	∞	∞	∞
1	{A，C}	5	3	6	7	∞
2	{A，C，B}	5	3	6	7	∞
3	{A，C，B，D}	5	3	6	7	9
4	{A，C，B，D，E}	5	3	6	7	9
5	{A，C，B，D，E，F}	5	3	6	7	9

从图中可知A到各点的距离为{5，3，6，7，9}

---

4、算法实现

结构体定义：

#define maxnum 100           //存放最大点数
#define int_max 65535        //存放正无穷
int dist[maxnum];            //最短距离
int prev[maxnum];            //前驱节点
typedef struct{
    char vexs[maxnum];       //存放节点
    int vexsum;              //存放节点数
    int edgsum;              //存放边数
    int arc[maxnum][maxnum]; //邻接矩阵
}graph;
void Dijkstra(graph *G,int v0);  //最短距离算法
void searchPath(int v0,int i);   //最短路径算法
void creategraph(graph *G);

创建图的方法void creategraph(graph* G)

{
    printf("%p\n", &dist);
    printf("%p\n", &G->arc);
    char v1, v2;
    int len;
    int x, y;
    x = y = 0;
    printf("请输入有向图的节点数及边数：");
    scanf_s("%d %d", &G->vexsum, &G->edgsum);
    getchar();
    printf("请输入节点的值：");
    //fflush(stdin);
    for (int i = 1; i <= G->vexsum; ++i) { 
        scanf_s("%c", &G->vexs[i],sizeof(G->vexs[i]));
        getchar();
    }
    for(int i=1;i<=G->vexsum;++i)               //初始化邻接矩阵
        for (int j = 1; j <= G->vexsum; ++j) {
            G->arc[i][j]=int_max;
        }
    for (int i = 1; i <= G->edgsum; ++i) {
        //fflush(stdin);
        printf("请输入边的顶点及权值：");
        scanf_s("%c %c %d", &v1,1, &v2,1, &len);
        getchar();
        for (int j = 1; j <= G->vexsum; ++j) {  //用字符查找对应的位置
            if (v1 == G->vexs[j])
                x = j;
        }
        for (int n = 1; n <= G->vexsum; ++n) {
            if (v2 == G->vexs[n])
                y = n;
        }
        G->arc[x][y] = len;        
    }
}

最短距离算法

void Dijkstra(graph* G, int v0) {
    int s[maxnum];
    for (int i = 1; i <= G->vexsum; ++i)
    {
        dist[i] = G->arc[v0][i];
        s[i] = 0;
        if (dist[i] == int_max)
            prev[i] = 0;
        else
            prev[i] = v0;
    }
    s[v0] = 1;
    dist[v0] = 0;
    for (int i = 1; i <= G->vexsum; ++i) {
        int u = v0;
        int temp = int_max;
        for (int j = 1; j <= G->vexsum; ++j) {
            if (dist[j] < temp && !s[j]){
                u = j;
                temp = dist[j];
            }
        }
        s[u] = 1;
        for (int j = 1; j <= G->vexsum; ++j)
        {
            if (!s[j] && G->arc[u][j] < int_max) {
                int newdist = dist[u] +G->arc[u][j];
                if (newdist < dist[j]) {
                    dist[j] = newdist;
                    prev[j] = u;
                }
            }
        }
    }
}

最短路径算法

void searchPath(int v0, int i) {
    int que[maxnum];
    int tot = 1;
    que[tot] = i;
    tot++;
    int temp = prev[i];
    while (temp != v0) {
        que[tot] = temp;
        tot++;
        temp = prev[temp];
    }
    que[tot] = v0;
    for (int i = tot; i >= 1; --i) {
        if (i != 1)
            printf("%d->", que[i]);
        else
            printf("%d\n", que[i]);
    }
 }

主函数

int main() {
   graph G;
   char dot;
   int v0=0;
   creategraph(&G);
   printf("请输入起始点：");
   scanf_s("%c", &dot,1);
   getchar();
   for (int j = 1; j<=G.vexsum; ++j) {
       if (dot == G.vexs[j])
           v0 = j;
   }
   Dijkstra(&G, v0);
   for (int i = 1; i <= G.vexsum; ++i) {
       
       if (dist[i] < int_max) {

       
           printf("%c到%c的最短距离为：%d\n",dot,G.vexs[i],dist[i]);
           printf("%c到%c的最短路径为:", dot, G.vexs[i]);
           searchPath(v0,i);
       } 
   }
}