OPTIMAL CONVERSION OF CONVENTIONAL ARTIFICIAL NEURAL NETWORKS TO SPIKING NEURAL NETWORKS 阅读总结

最新推荐文章于 2025-02-17 11:27:08 发布

原创最新推荐文章于 2025-02-17 11:27:08 发布 · 726 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #深度学习

Neuronal Dynamics 专栏收录该内容

13 篇文章

订阅专栏

OPTIMAL CONVERSION OF CONVENTIONAL ARTIFICIAL NEURAL NETWORKS TO SPIKING NEURAL NETWORKS 阅读总结

ABSTRACT
1.INTRODUCTION
2.PRELIMINARIES
3.CONVERSION EQUATION FROM ANN TO SNN
4.DECOMPOSITION OF CONVERSION ERROR
5.LAYER-WISE AND TOTAL CONVERSION ERROR
6.RELATED WORK
7.EXPERIMENTS
8.DISCUSSION
APPENDIX

ABSTRACT

主要工作：
通过递归归约到分层求和来分析转换误差
提出了一种新的策略管道:通过结合阈值平衡和软复位机制将ANN权重转移到目标SNN

效果：支持在几乎没有准确率损失的情况下，SNN模拟只需要传统方法十分之一的时间。

1.INTRODUCTION

ANN虽然有效但是需要大量能耗和内存空间，不容易在嵌入式平台部署
而SNN相对能耗低，内存少，有利于嵌入式平台部署。
主流获取SNN方法：
1.使用替代梯度反向传播直接进行有监督学习，在小数据集上有时表现较好，缺点是训练过程需要大量时间与内存且在大数据集不容易收敛。
2.ANN2SNN方法。SNN采用IF模型和软复位机制，局限性在于将同一次的输入信息相等地离散化，没有考虑不同的神经元的激活频率的变化。一般SNN很难通过较短的模拟序列传递信息，需要在精度与模拟序列长度之间权衡。
该论文主要工作：
1.理论分析了转换的过程，推导出了精确到每一层的可以优化的转换误差。（第4节）
2.提出了一种转换算法：在使用更短的模拟步长的情况下，有效的控制了源ANN和目标SNN之间的激活值的差异（第5节）
3.同时从理论和实验证明了该算法的有效性，并讨论了其推广的潜力（第7节）

2.PRELIMINARIES

该论文的方法对RELU函数进行了包括最大激活阈值设置和改变转折点的改进方式。
阈值设置使所有神经元能够在较短的时间内被激活
改变转折点的操作补偿了向下舍入引起的误差

这一节后面简要介绍了传统ANN2SNN方法，此处不再缀叙,框架如下图A
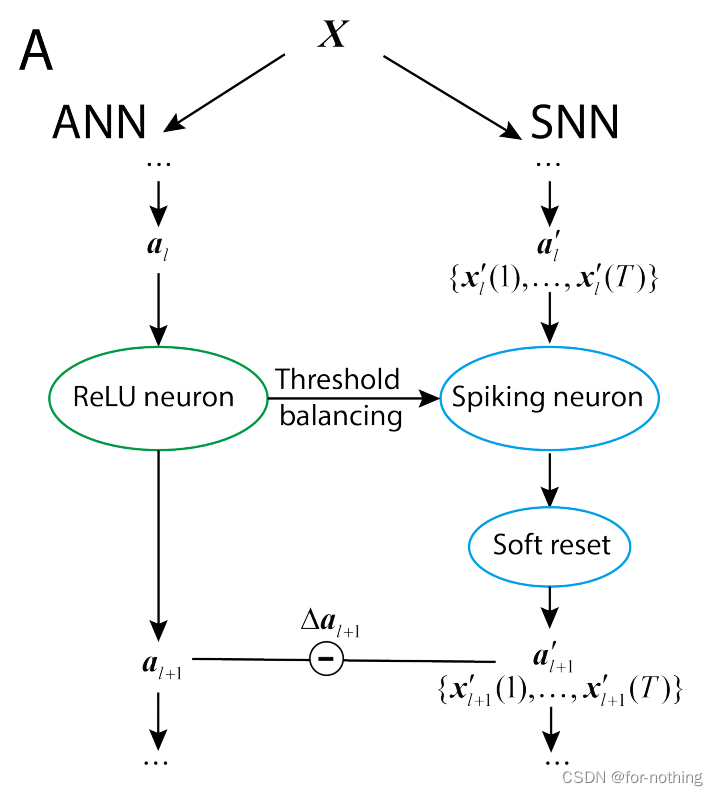
在这里插入图片描述

后面的论文中，首先推导出从源ANN到目标SNN的权值变换方程。(Part3)
接着证明了整体转换误差可以分解为每一层源激活值与目标输出频率之间的误差之和。(Part4)
最后，根据阈值平衡机制估计每一层的最优位移值，并用公式表示了总体转换误差。(Part5)

3.CONVERSION EQUATION FROM ANN TO SNN

参考我之前写的博客https://blog.youkuaiyun.com/for_none/article/details/128703352的推导，可以得到其中2.3节式子
$\phi^l(T)=\bm W^l\phi^{l-1}(T)-\frac{\bm v^l(T)-\bm v^l(0)}T$
这篇文章中用向量 $\bm a'_l$ 代替 $\phi^l$ 即SNN中的第l层每个神经元的平均输出，用向量 $\bm a_l$ 表示ANN中的第l层每个神经元的平均输出，用 $W_l$ 代替上式的 $W^l$ 表示l层与l+1层之间的权重
当我们取 $\bm v^l(0)=0$ 的时候有：
$\bm a'_{l+1}=W_l\bm a'_l-\frac{\bm v^l(T)}{T}$
引入阈值 $V_{th}$ ,由于当 $V_{th}$ 比ANN的最大激活值来的大的时候，剩余的 $\bm v^l(t)$ 小于 $V_{th}$ 不会对输出造成影响，所以定义 $h^{'}$ :
$\bm a'_{l+1} := h'(W_l\bm a'_l)=\frac{V_{th}}{T}clip(\lfloor\frac{W_l\bm a'_l}{V_{th}/T}\rfloor,0,T)$
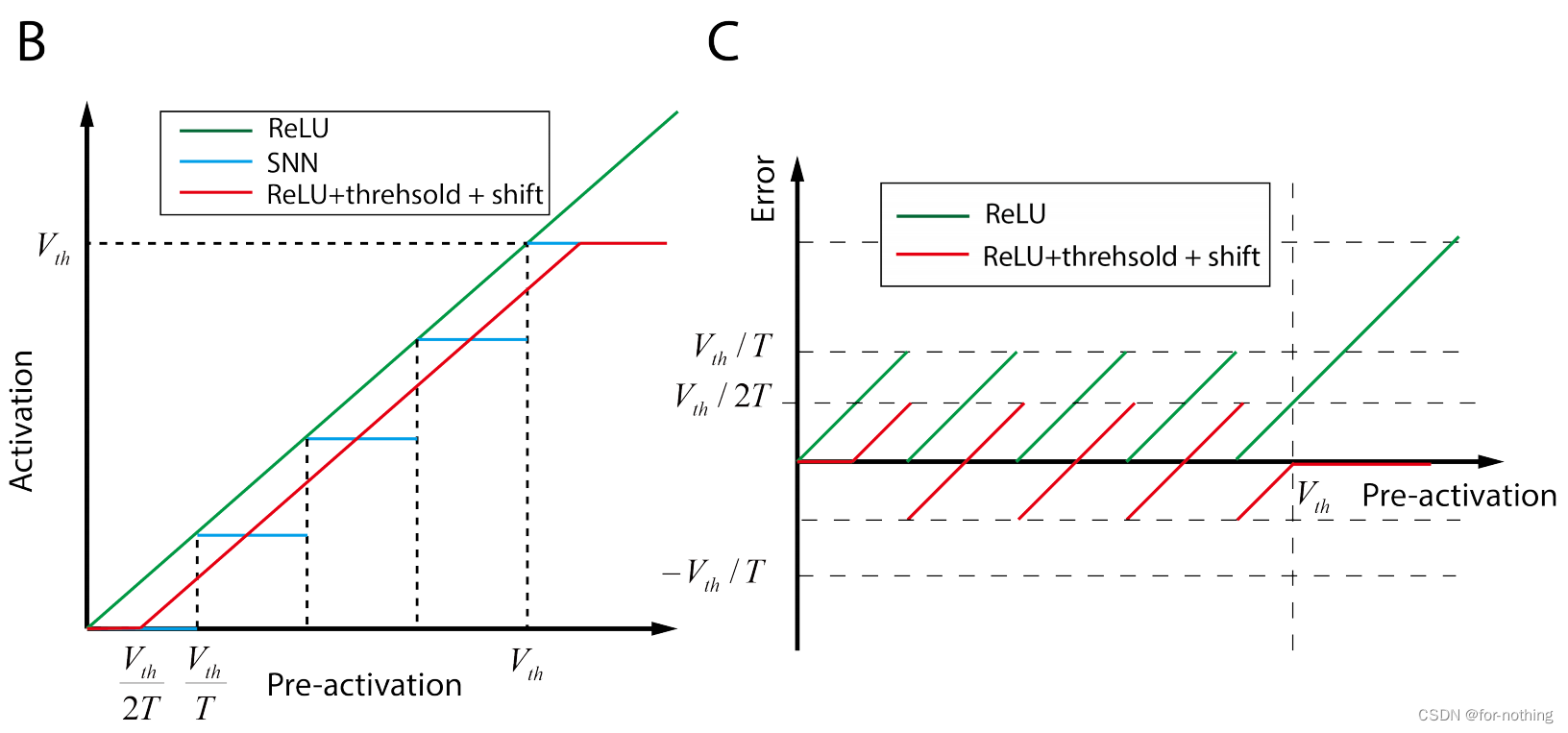
但是即使 $\bm a'_{l-1}$ 与 $\bm a_{l-1}$ 相同的时候， $\bm a'_l$ 与 $\bm a_l$ 也会有误差如图B，C
在这里插入图片描述

4.DECOMPOSITION OF CONVERSION ERROR

SNN的好坏由源ANN的好坏和转换产生的误差共同决定，此处仅讨论如何对后者进行优化。
我们定义损失函数L是关于最后一层输出的函数，由此定义转换误差：
$\Delta L=E[L(a'_L)]-E[L(a_L)]$
对于SNN中的第l层，我们可以用源ANN的激活函数h(·)反向近似其输出，得到：
$\bm a'_l=h'_l(W_l\bm a'_{l-1})=h_l(W_l\bm a'_{l-1})+\Delta\bm a'_{l-1}$
其中， $\Delta\bm a'_l$ 为ANN激活函数与SNN激活函数差异引起的误差。
源神经网络与目标SNN在第l层的总输出误差 $\Delta\bm a_l$ ，即激活 $\bm a_l$ 与 $\bm a'_l$ 的差值可近似为:
$\Delta\bm a_l:=\bm a'_l-\bm a_l=\Delta\bm a'_l+[h_l(W_l\bm a'_{l-1})-h_l(W_l\bm a_{l-1})]\approx\Delta\bm a'_l+B_lW_l\Delta\bm a_{l-1}$
其中最后一步近似是由一阶泰勒展开给出， $B_l$ 是 $h_l$ 的一阶导数的一维矩阵。
将总的转换误差 $\Delta L$ 在 $a_L$ 处展开可以得到：
$\Delta L\approx E[\bigtriangledown_{a_L}L\Delta\bm a_L]+\frac{1}{2}E[\Delta\bm a_L^TH_{\bm a_L}\Delta\bm a_L]$
其中 $H_{\bm a_L}$ 是L的黑塞矩阵。由于L是在源ANN上优化的（个人认识是ANN的此处L的斜率为零，因为是极值点），我们可以忽略这里的第一项（不是一定的）。因此，求出∆aL即可使第二项最小化，将上式子带入得到：
$E[\Delta\bm a_L^TH_{\bm a_L}\Delta\bm a_L]=E[\Delta\bm a_L'^TH_{\bm a_L}\Delta\bm a'_L]+E[\Delta\bm a_{L-1}^TB_LW^T_LH_{\bm a_L}W_LB_L\Delta\bm a_{L-1}]+2E[\Delta\bm a_{L-1}^TB_LW_L^TH_{\bm a_L}\Delta\bm a'_L]$
其中 $2E[\Delta\bm a_{L-1}^TB_LW_L^TH_{\bm a_L}\Delta\bm a'_L]$ 被证明可以忽略(参考此处文章)，同时采用近似 $H_{\bm a_{L-1}}=B_LW^T_LH_{\bm a_L}W_LB_L$ （参考此处文章的附录A和第三节，也可见下方补充1）可以得到：
$E[\Delta\bm a_L^TH_{\bm a_L}\Delta\bm a_L]\approx E[\Delta\bm a_L'^TH_{\bm a_L}\Delta\bm a'_L]+E[\Delta\bm a_{L-1}^TH_{\bm a_{L-1}}\Delta\bm a_{L-1}]=...=\sum_lE[\Delta\bm a_L'^TH_{\bm a_l}\Delta\bm a'_l]$
此处的 $H_{\bm a_l}$ 可以视为Fisher信息矩阵(参考此处文章)或者视为一个常数(参考此处文章,该文章中第五部分通过经验结果得到采取一个常数不会对结果造成很大影响)。
为简单起见，我们将其作为一个常数，将转换误差最小化的问题简化为每一层激活值差异的最小化的问题。

补充1:

在这里插入图片描述
其中 $h_\lambda = W_\lambda a_{\lambda-1}$
但是这里由于这里H是E对H求导而不是E对a求导，所以和我们不大一样，我重新书写了一下(后续的推导有一点不一样，前面一项就是我们需要的形式，而后面一项我还没搞清楚是怎么省略，后续会进行补充)
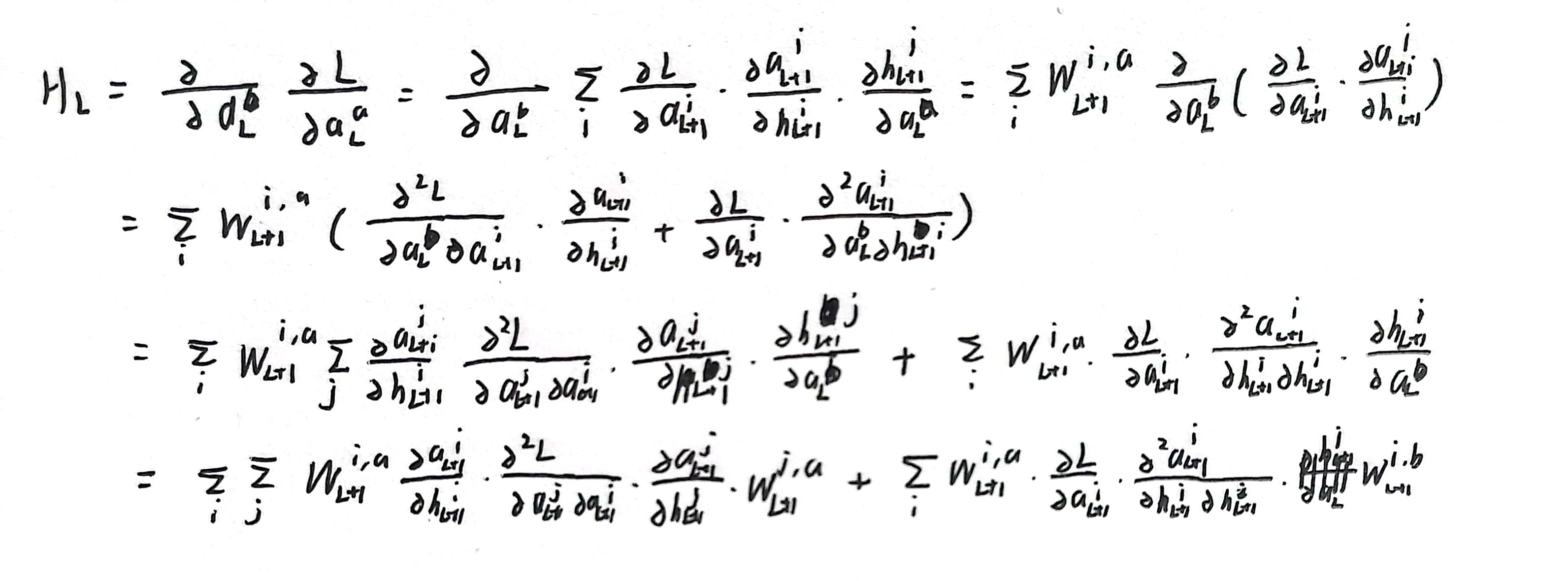
在这里插入图片描述

5.LAYER-WISE AND TOTAL CONVERSION ERROR

在前一节中，分析了最小化转换误差相当于最小化每一层上由ANN和SNN的不同激活函数引起的输出误差。
在这一节中，将进一步分析如何修改激活函数，以使分层误差最小化。
首先，我们考虑两种极端情况:1)阈值 $V_{th}$ 太大，以至于模拟时间T不够长，神经元无法发射脉冲;2)阈值 $V_{th}$ 太小，以至于神经元每次都出现脉冲，并且在模拟后积累了非常大的膜电位。对于这两种情况，剩余的电位包含大部分来自ANN的信息，几乎不可能从源ANN转换到目标SNN。为了消除这两种情况，我们使用阈值ReLU代替常规的ReLU，并将SNN中的阈值电压 $V_{th}$ 设置为ANN中ReLU的阈值 $y_{th}$ 。
接着，由于我们视 $H_{\bm a_l}$ 为一个常数，所以目标变为最小化 $E||\Delta\bm a'_l||^2$ 即 $E||h'_l(W_l\bm a'_{l-1})-h_l(W_l\bm a'_{l-1})||^2$ .
由图B和图C可以知道，尽管输入相同，但是 $h_l$ 和 $h'_l$ 之间仍然存在系统误差，我们通过添加位移项的方式解决，于是有：
$E_{\bm z}[h'_l(\bm z-\delta)-h_l(\bm z)]^2$ 我们假设 $\bm z=W\bm a'_{l-1}$ 均匀的分布在 $[\frac{(t-1)V_{th}}{T},\frac{tV_{th}}{T}]$ ,t=1,…,T
为了获得 $\delta$ 可以将上式化为： $\argmin_\delta\frac T2[(\frac{V_{th}}T-\delta)^2+\delta^2]$ ，由此得到 $\delta=\frac{V_{th}}{2T}$
由此总的误差： $\Delta L_{min}\approx\sum_lE[\Delta\bm a_L'^TH_{\bm a_l}\Delta\bm a'_l]\approx\frac{LV_{th}^2}{4T}$
最优位移可能与 $\frac{V_{th}}{2T}$ 不同。位移的作用是最小化源ANN输出与目标SNN之间的差异，而不是直接优化SNN的精度。因此，最优位移受到源ANN和目标SNN中激活值分布和过拟合水平的影响。
转化过程如下算法1:

在这里插入图片描述

6.RELATED WORK

此处非本文重点，所以略过。

7.EXPERIMENTS

7.1 ANN PERFORMANCE WITH THRESHOLD RELU

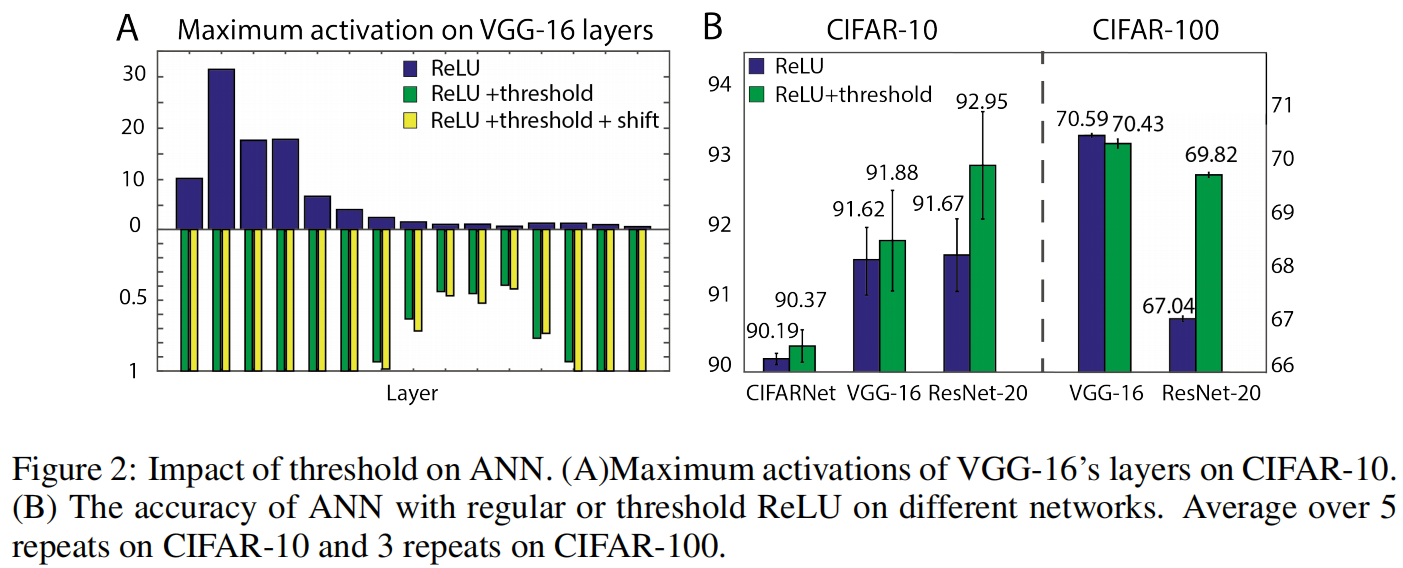
在这里插入图片描述
如图2，可以看到在加入阈值之后大部分数据的准确率都有提高（对CIFAR-10 $y_{th}=1$ ,CIFAR-100 $y_{th}=2$ ）
这些结果支持阈值ReLU可以合理地作为神经网络到SNN转换的来源。

7.2 IMPACT OF SIMULATION LENGTH AND SHIFT ON CLASSIFICATION ACCURACY

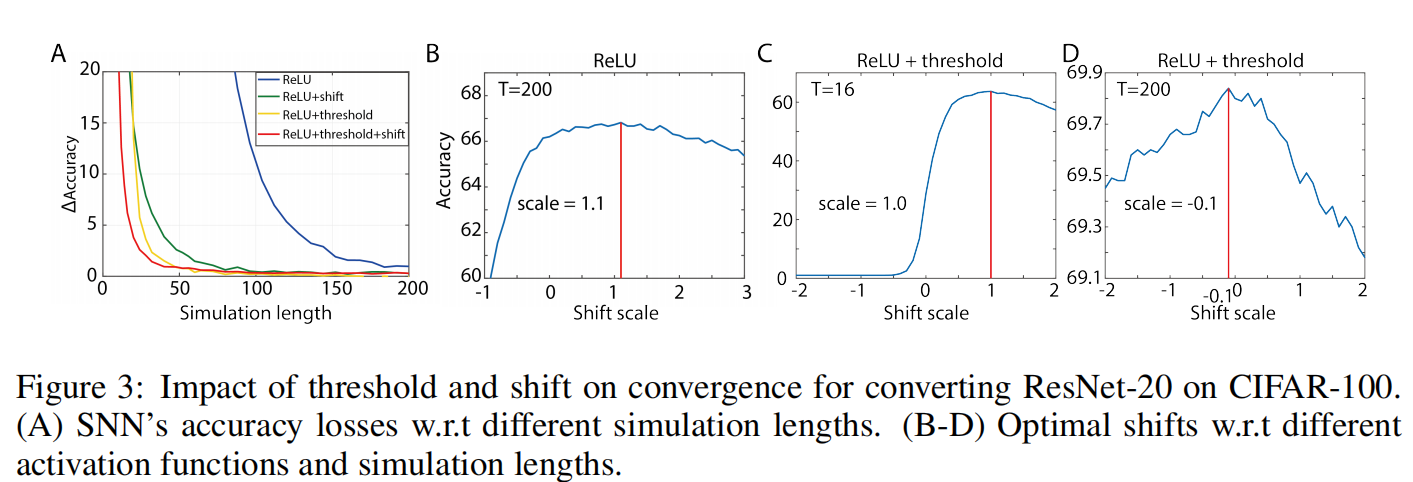
在这里插入图片描述
如图3实验表明了阈值和位移项对分类结果的准确性的影响（CIFAR-100， $y_{th}=2$ ）
图3A表明无论阈值和位移项单独还是同时应用，都会大大加快准确性收敛的速度，尤其当模拟长度T<50的时候两者结合效果最好。
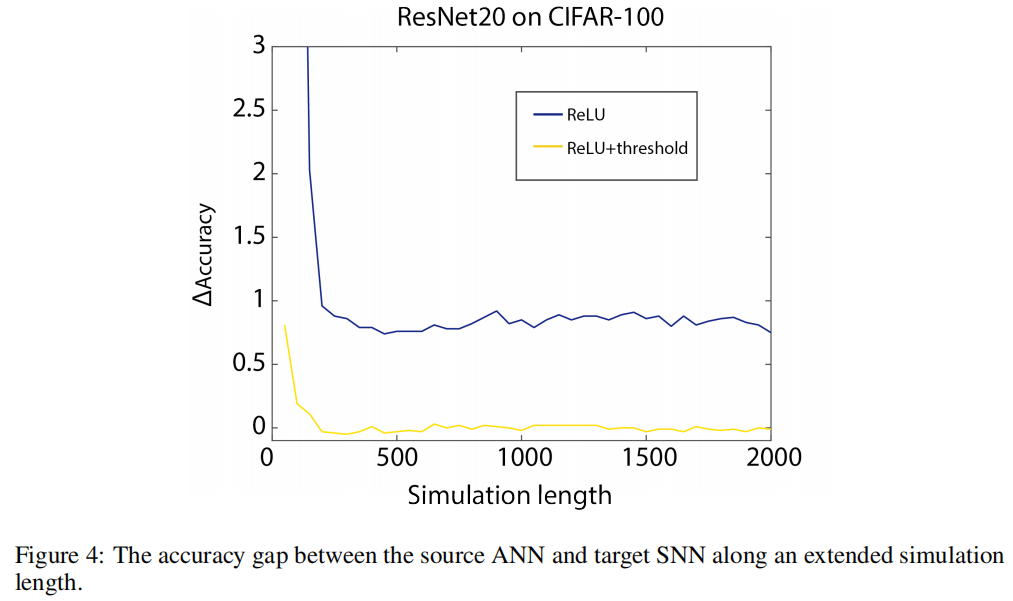
当ReLU具有阈值时，移位的工作方式不同。当模拟长度很短，比如T = 16时，转换可以带来巨大的好处如图3C。然而当仿真长度足够长时，移位不再有效，甚至可能会轻微损害精度如图3D，而仅增加阈值几乎可以消除原始阈值平衡方法中始终保持在零以上的转换误差。

7.3 COMPARISION WITH RELATED WORK

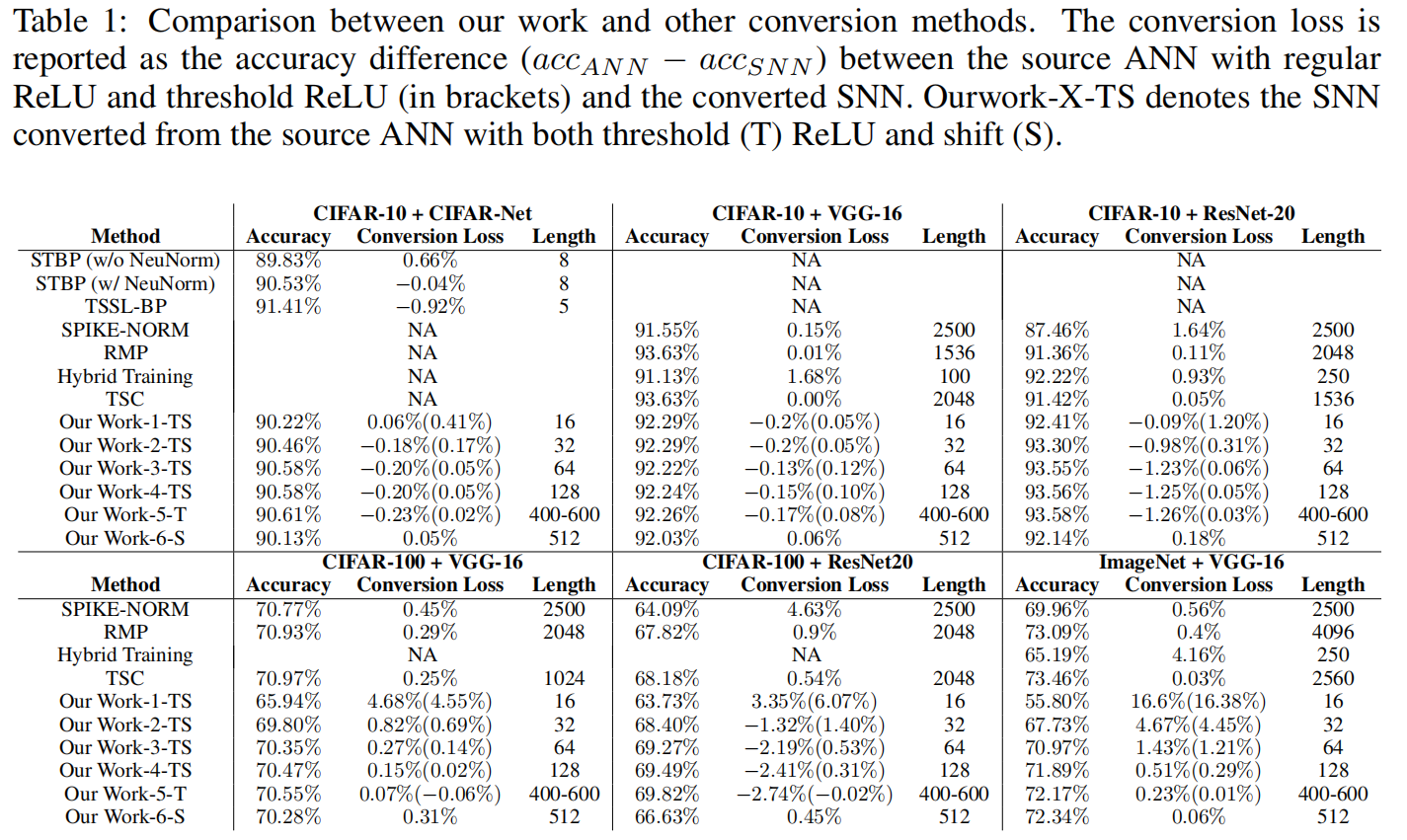
在这里插入图片描述
相对于直接训练的SNN虽然可以在更短的模拟步长内达到较好的效果，但是直接训练有很高的训练成本。
相对于其他ANN2SNN方法，该方法可以在较小的时间步长内达到很优秀的准确率。
这里便不再进行详细的数据结果解释。

8.DISCUSSION

先前的结果没有从理论上分析整个网路的转换误差，也没有考虑哪些类型的ANN更容易进行转换，该论文的工作填补了这一方面的空白，并用了一系列实验进行证明。
该论文1.对转换误差的理论分解为ANN-SNN转换提供了一个新的视角;2.证明了位移操作对于转换的必要性;3.极大缩短了转换所需的模拟长度，尤其是大型网络。

APPENDIX

附录部分仅记录一些标题与图片为了便于自己以后回想，感觉根据标题和图片已经能够读懂含义了，所以没有做过多解释,
A.1 NETWORK STRUCTURE AND OPTIMIZATION SETUP
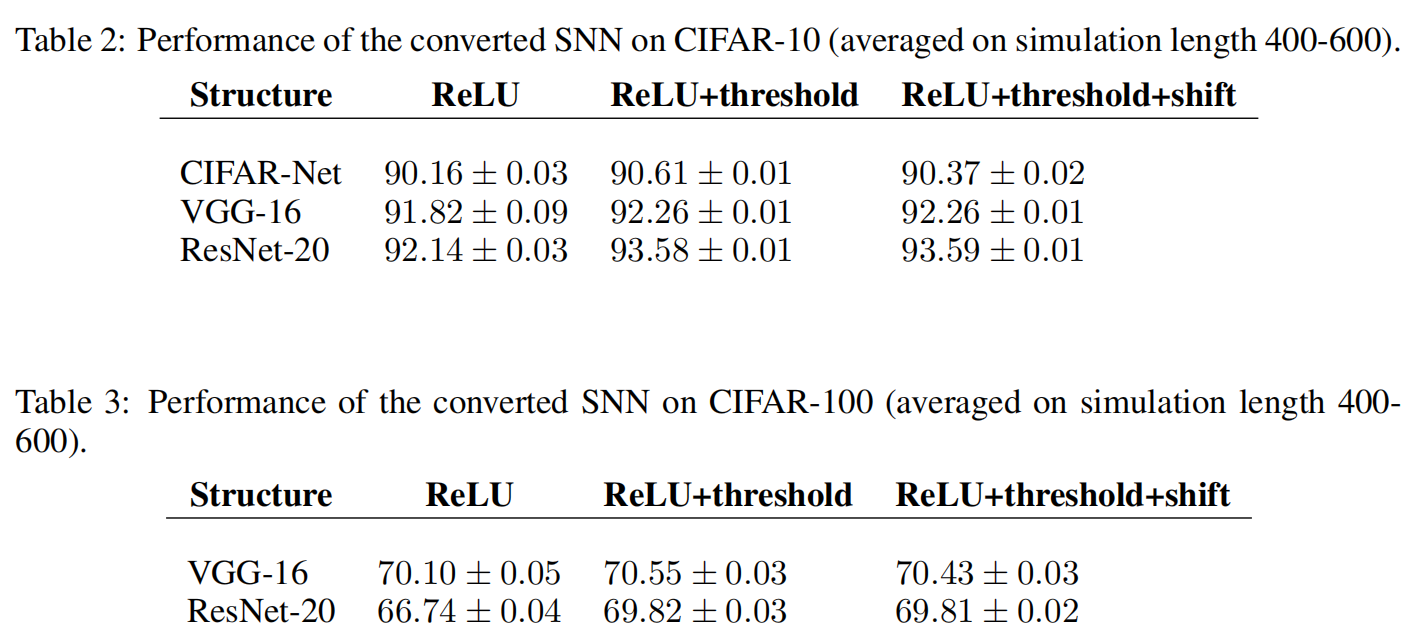
A.2 SNN PERFORMANCE WITH SIMULATION LENGTH 400-600
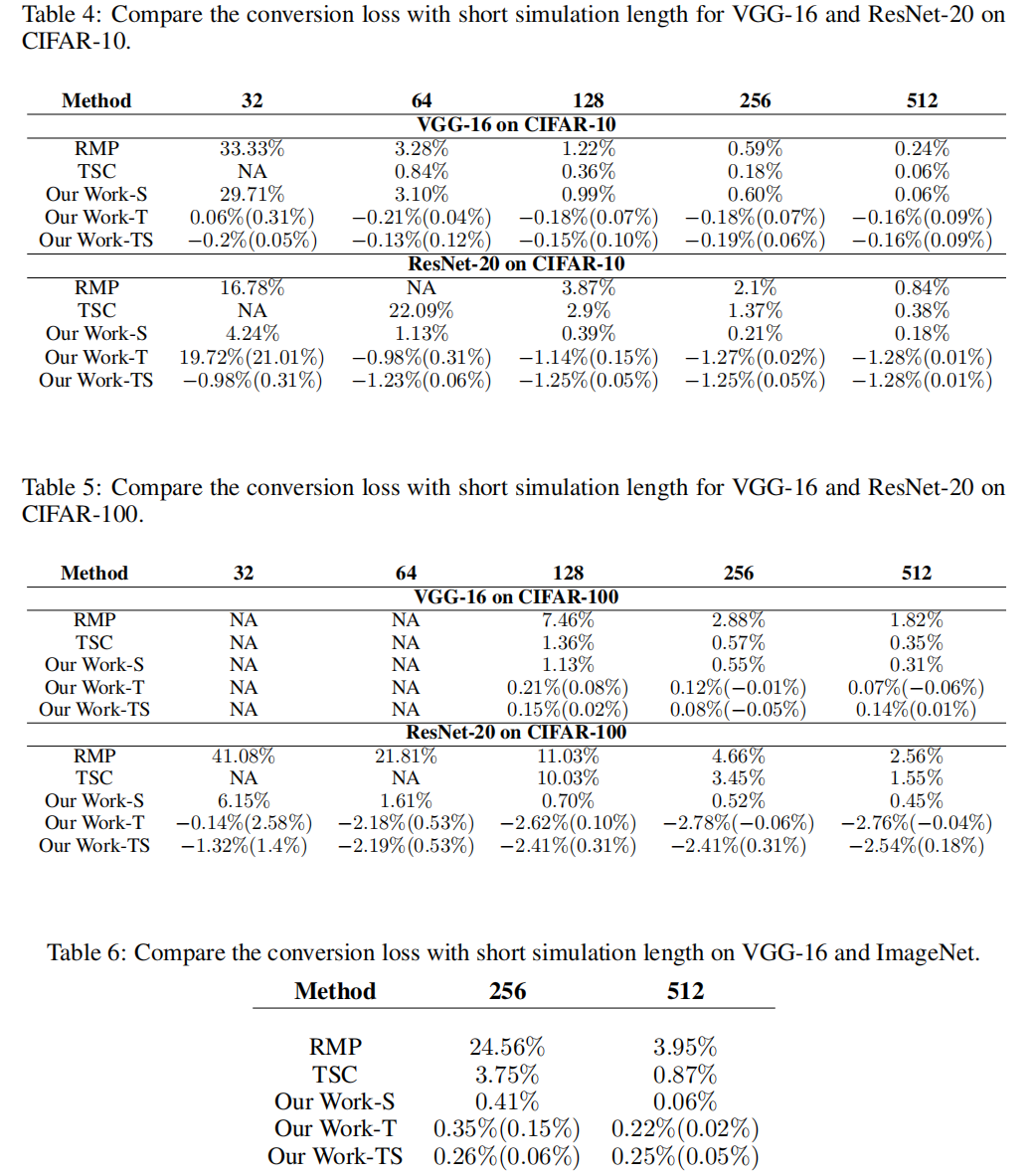
在这里插入图片描述
A.3 SNN PERFORMANCE WITH SHORT SIMULATION LENGTH

A.4 PERFORMANCE OF SNN CONVERTED FROM RNN
A.5 COMPARE THE PERFORMANCE ON LONG SIMULATION