5.1 前馈神经网络（PRML读书笔记）

  回归和分类的线性模型分别在第3章和第4章中讨论过了。它们基于固定⾮线性基函数${\varphi }_j(\text{x})$的线性组合，形式为

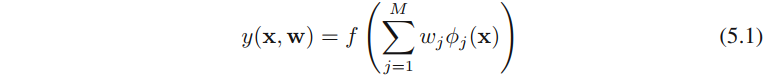
其中$f(\cdot )$在分类问题中是⼀个⾮线性激活函数，在回归问题中为恒等函数。我们的⽬标是推⼴这个模型，使得基函数${\varphi }_j(\text{x})$依赖于参数，从⽽能够让这些参数以及系数{$w_j$}在训练阶段调节。
  神经⽹络使⽤与公式（5.1）形式相同的基函数，例如如下形式的神经网络

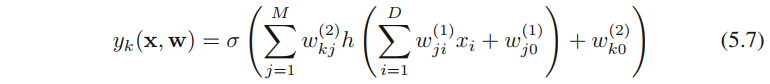
其中，⾮线性函数$h(\cdot )$通常被选为S形的函数，例如logistic sigmoid函数或者双曲正切函数。$w_{j0}^{(1)}$、$w_{k0}^{(2)}$称为偏置。可以通过定义额外的输⼊变量的⽅式将公式（5.7）中的偏置参数整合到权参数集合中，从而变为

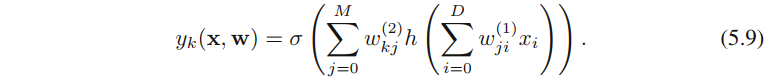
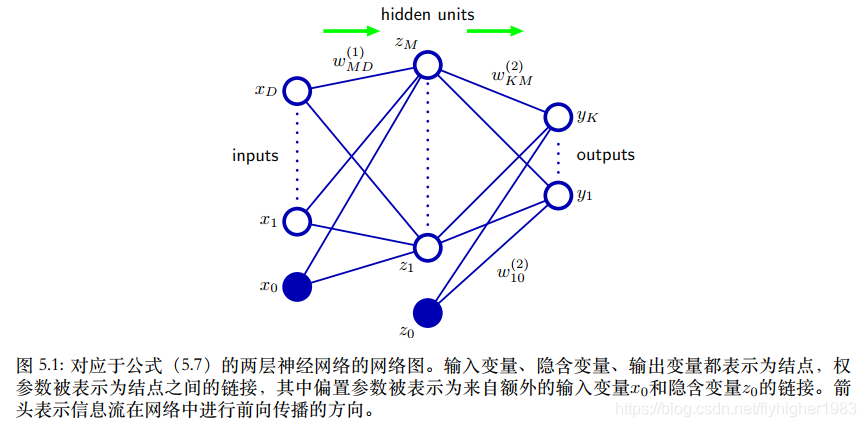
可以看出，公式5.9跟公式5.1形式上一样。$h({\sum }_{i=0}^D{w}_{ji}^{(1)}{x}_i)$、$\sigma (\cdot )$分别对应公式5.1中的${\varphi }_j(\text{x})$、$f(\cdot )$。公式5.7对应图5.1的两层神经网络，中间的{$z_0$、…、$z_M$}称作隐藏单元。公式5.7计算的过程可以看作信息通过⽹络的前向传播。