多层线性模型和面板数据模型笔记（待完善，持续更）

多层线性模型和面板数据模型笔记（待完善，持续更）

申明：部分内容参考网上优秀的热衷分享的作者，此篇文章仅作个人学习的综合整理，侵权自觉删掉。
引用的文章观点主要来自：
知乎：统计学中的「固定效应 vs. 随机效应」
连享会：Stata: 面板数据模型一文读懂

一、多层线性模型Hierarchical Linear Model

1 传统回归分析模型

$Y_i={\beta }_0+{\beta }_1{X}_i+{\epsilon }_i$

其中${\epsilon }_i\sim N(0,{\sigma }^2)$

基本假设-来源于伍德里奇教材P129：

线性于参数，随机抽样，不存在完全共线性，误差条件均值为零，误差同方差性，误差正态分布

2 多层数据

多层数据是指观测数据在单位上具有嵌套关系。

比如，学生嵌套于学校。

同一单位内的观测，具有更大相似性。

比如，同一学校的学生比其他学校的学生更具有相似性。

假设现在要考察学校教学设备对学生成绩的影响，在20所学校抽取1000名学生，那么可能有的学校为贵族学校，因此学生家长经济水平较高，可以缴纳更多设备费用，而另外的平民学校则负担不了额外的设备费用，因此，学生成绩受学校的教学设备影响，而学校设备又受学校整体经济水平影响。

多层数据违背了传统回归分析模型的残差相互独立假设，导致其得到的标准误估计不正确（太小）。

假如对个体水平上进行分析，比如每个学生，则假设同一班级的学生间相互独立，是不合理的。

加入对单位水平上进行分析，不如不同班级间的比较，则会丢失班级内学生个体间的差异的信息。

独立性不满足会带来标准误估计偏小从而导致犯第一类错误的概率偏大。

3 处理方式：建立HLM模型

将$Y_{i}j={\beta }_0+{\beta }_1{X}_{ij}+{\epsilon }_{ij}$ 改写成 $Y_{ij}={\beta }_0+{\beta }_1{X}_{ij}+u_j+r_{ij}$

其中 $u_j$ ，定义的是第 j 组的残差项，解释的是总截距和第 j 组的截距之间的差异

而 $r_{ij}$ 定义的是第 j 组第 i 个观测的残差项

特点：

1. HLM会把多层嵌套结构数据在因变量上的总方差进行分解：

   总方差 = 组内方差（Level 1）+ 组间方差（Level 2）

   $Var({\epsilon }_{ij})=Var(u_j)+Var(r_{ij})$

2. X 和 Y 之间的关系不依赖于 j （${\beta }_1$不依赖于 j）

模型的另一种表达：
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{split} …
现在用两个水平分析模型：

水平1即Level 1（如学生，组内的个体）：

$Y_{ij}={\beta }_{0j}+{\beta }_{1j}{X}_{ij}+{\epsilon }_{ij}$

$学生成绩={\beta }_0+{\beta }_1\ast 学校设备建设程度+r_{ij}$

水平2即Level 2（如学校，不同的单位）：

${\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{W}_{1j}+u_{0j}$

${\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{W}_{1j}+u_{0j}$

${\gamma }_{00}$和${\gamma }_{10}$表示截距和斜率的整体均值，用来描述总体情况的变化趋势。

${\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}学校整体经济水平+u_{0j}$

${\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}学校整体经济水平+u_{0j}$

包寒吴霜-知乎用户：我们还可以引入学校水平的自变量来对学校间的GPA均值差异进行解释，比如教师数量、教学经费……这些变量由于只在学校层面变化，对于每个学校内的每一个学生而言都只有一种可能的取值，因此必须放在Level 2的方程中作为群体水平自变量，而不能简单地处理为个体水平自变量——这也就是HLM的另一个存在的意义：可以同时纳入分析个体与群体水平的自变量。

在充分理解了HLM的原理之后再去理解其他统计方法就会比较轻松，尤其是在理解固定效应FE和随机效应RE这件事情上。但在HLM的话语体系中，我们不太直接说FE和RE，因为这两个词对于HLM而言太过于笼统

固定截距（fixed intercept）	随机截距（random intercept）	固定斜率（fixed slope）	随机斜率（random slope）
HLM中不存在，同理，面板数据模型中也不存在	HLM中常用	斜率在不同组内是相同的	斜率在不同组内是不同的

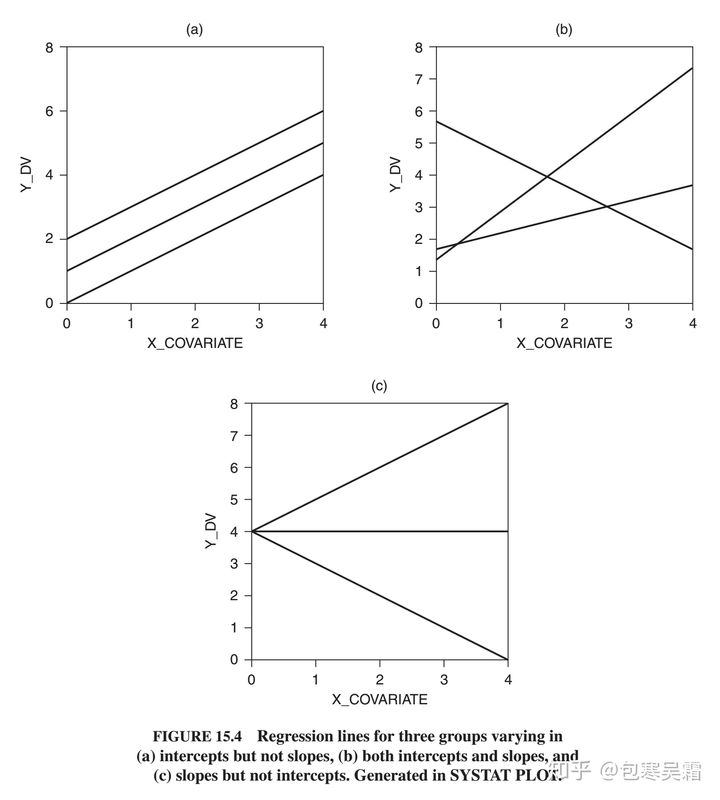
4 对固定效应和随机效应的理解

在HLM的框架下探讨固定效应还是随机效应，更多的是指**「斜率」为固定还是随机**。

二、面板数据Panel Data Model

1 面板数据基本定义

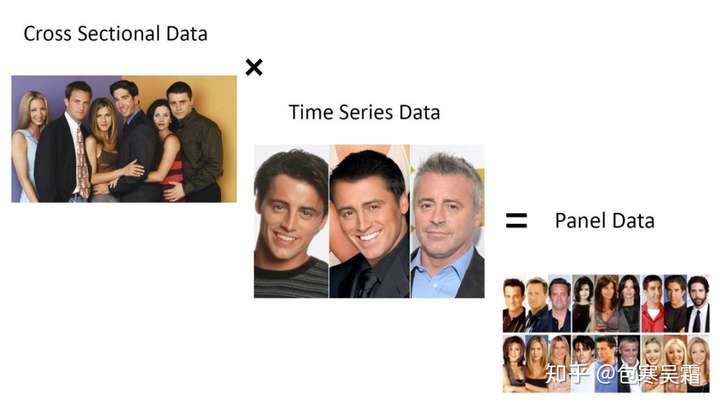
面板数据可以理解为由时间维度和横截面维度组成的数据。

在经济学里，可以是研究不同省份在不同年份的经济增长受创新投入的影响。

司马懿-知乎用户：面板数据和横断面数据的区别就在于，面板数据多了一个时间的维度。也就是说，一个人的数据不但能够横向的和同一时间的其他人相比，也能够纵向的和之前之后的自己相比。

如果把一个人在不同时间的数据称为一组数据的话，那么前者称为组间差异，后者称为组内差异。

面板数据的优点是既可以考虑到横截面数据存在的共性，也可以分析模型中横截面因素的个体特殊效应。

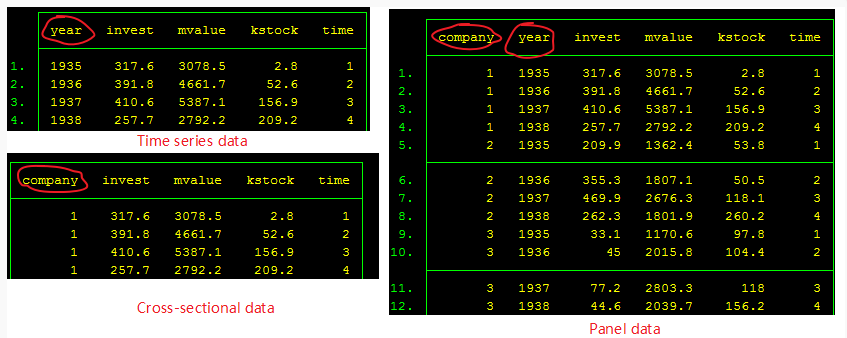
郭凯明-连享会：欲研究影响企业利润的决定因素，我们认为企业规模 (截面维度)和技术进步(时间维度)是两个重要的因素。

截面数据仅能研究企业规模对企业利润的影响程度，时间序列数据仅能研究技术进步对企业利润的影响。

2 最简单的面板数据模型介绍

（1）符号含义规范

$y_{it}$——因变量在横截面 i 和时间 t 上的数值

$x_{it}^j$——第 j 个解释变量在横截面 i 和时间 t 上的数值

为方便讨论，一般假设有 K 个解释变量，N个横截面，T个时间指标

记第 i 个横截面的数据

${\mathbf{y}}_i={\left[\begin{array}{c}{y}_{i1}\\ y_{i2}\\ ⋮\\ y_{iT}\end{array}\right]}_{T\times 1}$ ${\mathbf{X}}_i={\left[\begin{array}{ccccc}{X}_{i1}^1& X_{i2}^2& \cdots & X_{1k}^K& \\ X_{i2}^1& X_{i2}^2& \cdots & X_{2k}^K& \\ ⋮& ⋮& ⋮& & ⋮\\ X_{iT}^1& X_{iT}^2& \cdots & X_{iT}^K& \end{array}\right]}_{T\times K}$ ${\mathbf{\mu }}_i={\left[\begin{array}{c}{\mu }_{i1}\\ {\mu }_{i2}\\ ⋮\\ {\mu }_{iT}\end{array}\right]}_{T\times 1}$

再记

$\mathbf{y}={\left[\begin{array}{c}{\mathbf{y}}_1\\ {\mathbf{y}}_2\\ ⋮\\ {\mathbf{y}}_N\end{array}\right]}_{N\cdot T\times 1}$ $\mathbf{X}={\left[\begin{array}{c}{\mathbf{X}}_1\\ {\mathbf{X}}_2\\ ⋮\\ {\mathbf{X}}_N\end{array}\right]}_{N\cdot T\times K}$ $\mathbf{\mu }={\left[\begin{array}{c}{\mathbf{\mu }}_1\\ {\mathbf{\mu }}_2\\ ⋮\\ {\mathbf{\mu }}_N\end{array}\right]}_{N\cdot T\times 1}$ $\mathbf{\beta }={\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_K\end{array}\right]}_{K\times 1}$

（2）建立简单面板数据模型

建立以下用矩阵形式表达的面板数据模型：
$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\mathbf{\mu }$$
基于这个模型，对系数 $\mathbf{\beta }$ 和随机误差项 $\mathbf{\mu }$ 进行不同假设，可以衍生出不同的面板数据模型。

（3）对误差项${\mathbf{\mu }}_{it}$ 的拆分

为了分析每个个体的特殊效应，可对${\mathbf{\mu }}_{it}$ 设定：

${\mathbf{\mu }}_{it}={\mathbf{\alpha }}_i+{\mathbf{\epsilon }}_{it}$

${\mathbf{\alpha }}_i$ 代表第 i 个个体的特殊效应，反映了不同个体之间的差别。

郭凯明-连享会：${\mathbf{\alpha }}_i$ 不随时间改变，如个人的消费习惯、企业文化和经营风格等

个人理解：这里讨论的个体应该是以横截面为个体。研究不同省份在不同年份的经济增长受创新投入的影响中，不同的省份就是不同的个体。

再如要研究影响一个人工资的因素，除了学历、工作经验年数外，还有不可测的变量如关系和能力，这些都是一些个人的异质性因素，即${\mathbf{\alpha }}_i$

如果${\mathbf{\alpha }}_i$和${\mathbf{X}}_{it}$ 相关，即$corr({\mathbf{\alpha }}_i,{\mathbf{X}}_{it})\ne 0$，则该模型为固定效应模型。若二者不相关，那就是随机效应模型。

郭凯明-连享会：固定效应模型假设个体效应在组内是固定不变的，个体间的差异反映在每个个体都有一个特定的截距项上； 随机效应模型则假设所有的个体具有相同的截距项， 个体间的差异是随机的，这些差异主要反应在随机干扰项的设定上。

固定效应分类	说明
个体固定	对于不同的时间序列（个体）只有截距项不同的模型：从时间和个体上看，面板数据回归模型的解释变量对被解释变量的边际影响均是相同的，而目除模型的解释变量之外，影响被解释变量的其他所有（未包括在回归模型或不可观测的）确定性变量的效应只是随个体变化而不随时间变化。
时间固定	时点固定效应模型就是对于不同的截面（时点）有不同截距的模型。如果确知对于不同的截面，模型的截距显著不同，但是对于不同的时间序列（个体）截距是相同的，那么应该建立时点固定效应摸型：
双固定	时点个体固定效应模型就是对于不同的截面（时点）、不同的时间序列（个体）都有不同截距的模型。如果确知对于不同的截面、不同的时间序列（个体）模型的截距都显著不相同，那么应该建立时点个体固定效应模型

3 固定效应模型

（1）假设

固定模型中假定

${\mathbf{\mu }}_{it}={\mathbf{\alpha }}_i+{\mathbf{\epsilon }}_{it}$ 的${\mathbf{\alpha }}_i$ 对每一个个体是固定的常数。

注：${\alpha }_1$，${\alpha }_2$，`···，${\alpha }_N$是不全相等的。

郭凯明-连享会：当对所有的 i , ${\mathbf{\alpha }}_i$ 均相等时，模型退化为混合数据模型 ( Pooled OLS )。

（2）检验方法

Hausman检验——$H_0:{\alpha }_i与X_{it}不相关$

若有证据拒绝此零假设，则可以判断出该模型需要采用固定效应模型。

4 问题集

问题1：
您好，请问一下面板数据回归时候加时间效应与不加时间效应，核心解释变量符号不一样，是怎么回事?

回答1：
面板数据模型中，控制时间效应后，此时的估计系数是排除了随时间变化的影响因素后的结果。相对来说，此时的结果更为可信。

问题2：
请问一下面板数据回归一定要加时间效应吗？不加可以吗？
谢谢老师

回答2：
个人建议，采用面板数据时，最好控制时间固定效应。当然这个也不是绝对的，我也看到有文献提供的代码里，并没有加时间固定效应。个人的理解，关键还是看你的被解释变量是否随时间变化，比如经济增长速度、产业结构系数等，在中国现阶段的情况下，这些变量一般是随着时间变化的，建议加上时间固定效应；如果你的被解释变量基本不随时间变化，我个人觉得这种情况下，加上时间固定效应与否，对你的结果影响都不大。

问题3：

面板不是还有个随机效应嘛？

回答3：

我只能说，你是看过书的人，所以才知道随机效应。其实随机效应压根就没什么用处。有人信誓旦旦说可以用hausman来检验。我只能告诉你，这检验压根就不可靠。可靠也是理论上可靠，实践上根本没人信。

最权威的建议就是：当你无法判断该用固定效应还是随机效应的时候，选择固定效应更可靠。随机效应不是任何时候都可以做，但是固定效应是任何时候都可以做。所以你知道该怎么做了吧。

4 stata操作

目前Stata已有许多相关面板数据模型命令，包括(不限于)：

- `xtreg` :普通面板数据模型，包括固定效应与随机效应
- `xtabond/xtdpdsys/xtabond2/xtdpdqml/xtlsdvc`：动态面板数据模型
- `spxtregress/xsmle`: 空间面板数据模型
- `xthreg`:面板门限模型
- `xtqreg/qregpd/xtrifreg`: 面板分位数模型
- `xtunitroot`: 面板单位根检验
- `xtcointtest/ xtpedroni/xtwest`: 面板协整检验
- `sfpanel`: 面板随机前沿模型
- `xtpmg/xtmg`：非平稳异质面板模型

备注

自由度

（degree of freedom，缩写为df）

可以简单地理解为可以独立变化的数据量。

计算公式是：$df=总变量数-衍生量数$

具体以例子理解。

在 $a+b=6$中，df=1，因为只有一个数据量 a 可自由变化，b 会受 a 的选值所限制。$df=2-1=1$

估计总体的平均数，所用统计量为样本平均数$\mu$，当样本总量为n，由于相对样本平均值无其他衍生量，因此$df=1$。但是如果估计总体方差，所用统计量是样本方差$s^2$, 需要用到样本平均数$\mu$，相对样本方差只有一个衍生量，因此$df=n-1$。

在t检验中，$t=\frac{\hat{\beta }}{SE}$，假设样本总量为n，同时相对t统计量需要两个衍生量$\hat{\beta }$和$SE$，所以