【暖*墟】 #图论# 二分图匹配

一、二分图的匹配

对于一个二分图G的子图M,若M的边集E的任意两条边都不连接同一个顶点，

则称M为G的一个匹配。即：“任意两条边没有公共端点”的边的集合。

---

二、最大匹配

对于二分图G的一个子图M，若M为其边数最多的子图，则M为G的最大匹配。

增广路：也称增广轨或交错轨。若P是图G中【一条连通两个未匹配顶点的（长）路径】，

属于M的边和不属于M的边（已匹配和待匹配的边）在P上交替出现（一个属于一个不属于...），

则P为M的一条增广路径。（相当于是，新加入一个节点，找到它能得到匹配的修改路径，那么len++）

(即：有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行)。

---

①初始状态。

当前已有边(1,1')和(4,3')属于M。

---

②找到一条增广路径P。

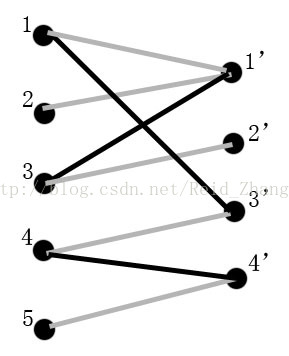
如图，增广路径P为：(3 - 1' - 1 - 3' - 4 - 4')。

其中，不属于M的路径有：(3, 1')、(1, 3')和(4, 4')，属于M的路径有(1‘, 1)和(3', 4)。

显然，在上面的路径P中，不属于M的路径和属于M的路径是交替出现的。

即：[3-1'(蓝), 1'-1(黑), 1-3'(蓝), 3'-4(黑), 4-4'(蓝)]。

---

③对第②步中的图进行取反。

将原来属于M的路径去除，将原来不属于M的路径加入M中。

即：蓝色的边变成黑色，黑色的边变成蓝色。

---

④增广路更新匹配完成。

---

由增广路的定义我们可以推出下述三个结论：

1. P的路径长度必定为奇数，交替的第一条边和最后一条边都不属于M。
2. 如果有增广路径，经过【取反操作】可以得到更大的匹配M’，边数为M的边数+1。

3. M为G的最大匹配当且仅当【不存在】相对于M的【增广路径】。

---

三、匈牙利算法

1、算法描述

    建立有向图G，分为二分图的左侧和右侧。
    优先选择左侧序号更小的、连接可能的边。
    对于两个点的目标点“冲突”的时候，采取“协商”的办法。
    即序号小的连接可能连接的另一条边。
    若“协商”失败，则序号较大的点放弃这条边，继续寻找。

具体情况如下：

1）如果（左侧）后来的和以前的发生矛盾，则以前的优先退让。

2）如果以前的退让之后没有连边，则以前的拒绝退让，新来的去寻找下一个匹配。

3）如果新来的谁也匹配不上了，那放弃这个新来的节点。

• 注意：根据交叉路原理容易证明每一条增广路的起点和终点分属不同点集。
• 因为如果从偶数次所到位置的下一次走匹配边，意味着找不到选择点。
• 所以左右是对称的，每次找增广路时都可以直接从左边的节点开始dfs。

---

2、代码实现

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<string>
#include<cmath>
using namespace std;
typedef long long ll;

/*【洛谷p3386】二分图匹配
给定一个二分图，结点个数分别为n,m，边数为e，求二分图最大匹配数。 */

void reads(int &x){ //读入优化（正负整数）
    int fx=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=fx; //正负号
}

const int N=5000019;

int n,m,num_e,x,y,ans=0,tot=0;
int match[N],head[N]; bool vis[N];

struct node{ int ver,nextt; }e[N];

void add(int x,int y){
    e[++tot].ver=y; e[tot].nextt=head[x]; head[x]=tot;
}

bool dfs(int x){
    for(int i=head[x];i;i=e[i].nextt) //寻找连边
        if(!vis[e[i].ver]){ //当前右节点在新左节点的匹配中未访问过
            vis[e[i].ver]=true; //标记这个非匹配点
            if(!match[e[i].ver]||dfs(match[e[i].ver])){ //如果原匹配的点可以让位
                match[e[i].ver]=x; return true; //左节点x可以占用这个右节点y
            }
        } return false;
}

int main(){
    reads(n),reads(m),reads(num_e);
    for(int i=1;i<=num_e;i++){
        reads(x),reads(y); //↓判断是否在范围内
        if(x>=1&&y>=1&&x<=n&&y<=m) add(x,y); //连边
    } for(int i=1;i<=n;i++) //寻找加入左侧每个节点时会不会有路径更新
        memset(vis,false,sizeof(vis)),ans+=dfs(i); //计算最大匹配边数
    printf("%d\n",ans); return 0;
}

---

四、完备匹配和多重匹配

【二分图的完备匹配】两侧节点一一对应。

• 二分图左右节点数相同，均为n个。且最大匹配包含n条匹配边。

【二分图的多重匹配】多重最大匹配 与 多重最优匹配。

• 二分图匹配中一个点可以和多条匹配边相关联，但有上限。
• 即：Li表示点i最多可以和多少条匹配边相关联。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                     ——时间划过风的轨迹，那个少年，还在等你。