每天算法 -- serialize and deserialize binary tree - medium

Google:

Given the root to a binary tree, implement serialize(root), 

which serialize the tree into a string, and deserialize(s), which deserialize the string back into the tree.

For example, given the following Node class

class Node:
    def __int__(self, val, left=None, right=None)
        self.val = val
        self.left = left
        self.right = right

The following test should pass:

node = Node('root', Node('left', Node('left.left')), Node('right'))

assert deserialize(serialize(node)).left.left.val == 'left.left' 

分析：所有的二叉树的题，都要利用递归的思想来解。

这个题难就难在如何巧妙的找到二叉树正确的序列化表示。

栈/函数调用 ，二叉树 -->递归， 想到这里，我不由得想到了计算器。计算器输入的其实就是一串字符串，然后输出结果，对于复杂的结合律，不就是通过栈/树来解决的吗？那这里为什么不能沿用它的思想呢？

树的两个左右子树不就是操作符的两个操作数吗？

对于以下的这颗树：

 

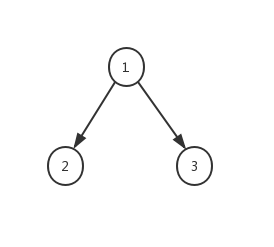
用()表示结点的子树，空格表示元素之间的分隔，那么，用 1 (2  () ())  (3 () ()), 我们完全可以用这种表示来表达一个树。为了简化起见，我们将空的子树()转化成 #， 那么二叉树就被简化成 1 2 # # 3 # #. 

好，那如何重新变成二叉树呢？

1 2 # # 3 # #

deserialize同样需要递归，那么如何设计这个递归函数呢？输入是字符串，返回则是树的结点。

算法逻辑：

对于该字符串，如果找到的第一个元素是#， 直接返回空，并将字符串关于#的那部分裁掉。若不是#，则新建一个结点，将元素的值存储到这个结点上，并对剩余的字符串递归调用生成该结点的左子树和右子树。

同样，代码附上，以供参考：

#include <iostream>
#include <string>

class BinaryTree
{
public:
    BinaryTree(std::string val, BinaryTree *left = nullptr, BinaryTree *right = nullptr)
    {
        this->val = val;
        this->left = left;
        this->right = right;
    }
    ~BinaryTree()
    {
        delete this->left;
        delete this->right;
    }
    
    std::string serialize()
    {
        std::string retVal = this->val;
        retVal += this->left ? (" " + this->left->serialize()) : " #";
        retVal += this->right ? (" " + this->right->serialize()) : " #";
        return retVal;
    }

    BinaryTree* deserialize(std::string& val)
    {
        if(val.empty())
            return nullptr;
        BinaryTree *retVal = new BinaryTree("");

        int pos = 0;
        pos = val.find_first_of(" ", pos);
        std::string element = val.substr(0, pos);
        val = val.substr(pos+1, val.length() -pos -1);

        if(element == "#")
            return nullptr;
        retVal->val = element;

        retVal->left = deserialize(val);
        retVal->right = deserialize(val);

        return retVal;
    }

private:
    std::string val;
    BinaryTree* left = nullptr;
    BinaryTree* right = nullptr;
}; 

int main()
{
    BinaryTree *biTree = new BinaryTree("1", new BinaryTree("2"), new BinaryTree("3"));
    std::string encodedBinaryTree = biTree->serialize();
    std::cout << "serialize: " + encodedBinaryTree << std::endl;
    BinaryTree * deBiTree = biTree->deserialize(encodedBinaryTree);
    std::cout << "serialize deserialized: " + deBiTree->serialize() << std::endl;

    delete biTree;
    delete deBiTree;
    return 0;
}