最小生成树

什么是最小生成树(Minimum Spanning Tree)

1、是一棵树

无回路，并且|v|个顶点一定有|v|-1条边

2、是生成树

包含全部顶点，并且|v|-1条边都在图中

3、边的权重最小

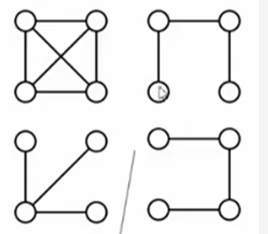
向生成树中任意加一条边都一定构成回路。

最小生成树算法

1、Prim最小生成树算法

Description

Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course.
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms.
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm.
The distance between any two farms will not exceed 100,000.

Input

The input includes several cases. For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem.

Output

For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms.

Sample Input

4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0

Sample Output

28

---

import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;


public class Main {
	static final int N = 101;
	static final int INF = 0x3f3f3f3f;
	static int G[][] = new int[N][N];
	static int dist[] = new int[N];
	static int path[] = new int[N];
	static int vis[] = new int[N];
	static int n,ans;
	static int s,t;
	
	static void Init() {
		ans = 0;
		s = 0;
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < n; j++) {
				if(i == j) G[i][j] = 0;
				else G[i][j] = INF;
			}
		}
		
	}
	
	static void Prim()
	{
		for(int i = 0; i < n; i++) {
			dist[i] = G[s][i];
			path[i] = -1;
		}
		vis[s] = 1;
		for(int i = 0; i < n; i++) {
			int min = INF, v = -1;
			for(int j = 0; j < n; j++) {
				if(vis[j] == 0 && dist[j] < min) {
					min = dist[j];
					v = j;
				}
			}
			if(v == -1) break;
			ans += min;
			vis[v] = 1;
			for(int k = 0; k < n; k++) {
				if(vis[k] == 0 && G[v][k] < dist[k]) {
					dist[k] = G[v][k];
					path[k] = v;
				}
			}
		}
		System.out.println(ans);
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		Init();
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < n; j++) {
				G[i][j] = sc.nextInt();
			}
		}
		Prim();
	}
	
}

2、Kruskal最小生成树算法

Description

Andrew is working as system administrator and is planning to establish a new network in his company. There will be N hubs in the company, they can be connected to each other using cables. Since each worker of the company must have access to the whole network, each hub must be accessible by cables from any other hub (with possibly some intermediate hubs).
Since cables of different types are available and shorter ones are cheaper, it is necessary to make such a plan of hub connection, that the maximum length of a single cable is minimal. There is another problem — not each hub can be connected to any other one because of compatibility problems and building geometry limitations. Of course, Andrew will provide you all necessary information about possible hub connections.
You are to help Andrew to find the way to connect hubs so that all above conditions are satisfied.

Input

The first line of the input contains two integer numbers: N - the number of hubs in the network (2 <= N <= 1000) and M - the number of possible hub connections (1 <= M <= 15000). All hubs are numbered from 1 to N. The following M lines contain information about possible connections - the numbers of two hubs, which can be connected and the cable length required to connect them. Length is a positive integer number that does not exceed 106. There will be no more than one way to connect two hubs. A hub cannot be connected to itself. There will always be at least one way to connect all hubs.

Output

Output first the maximum length of a single cable in your hub connection plan (the value you should minimize). Then output your plan: first output P - the number of cables used, then output P pairs of integer numbers - numbers of hubs connected by the corresponding cable. Separate numbers by spaces and/or line breaks.

Sample Input

4 6
1 2 1
1 3 1
1 4 2
2 3 1
3 4 1
2 4 1

Sample Output

1
4
1 2
1 3
2 3
3 4

---

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1001;
const int INF = 0x3f3f3f3f;
int n,ans,m,num;
//ans连接计划中单个电缆的最大长度 num 统计生成树中的结点数 
int f[N];  //并查集
int Num[15001]; //用来记录最小生成树中的结点 
struct map{  //邻接表 
	int x,y; //端点 
	int w;  //边的权值 
}G[15001];

int cmp(struct map a, struct map b)
{
	return a.w < b.w;
}
void Init()
{
	ans = num = 0;
	for(int i = 0; i <= n; i++) f[i] = i; //并查集初始化为自身
	 
}
int find(int x)  //求每个结点的根结点 路径压缩 
{
	return f[x] == x ? x : f[x] =find(f[x]); 
}
void Union(int x1, int x2)  //结点合并 
{
	int p1 = find(x1);
	int p2 = find(x2);
	if(p1 != p2) f[p1] = p2;
}

void Kruskal()
{
	//让边权小的排在前面 
	sort(G,G+m,cmp); 
	int cnt = 0;  //加入生成树中的边 
	for(int i = 0; i < m; i++){
		if(find(G[i].x) != find(G[i].y)){ //如果x和y不连通,就加入生成树
			cnt++; 
			Union(G[i].x, G[i].y);
			Num[num++] = i;
			ans = G[i].w; 
		}	
		if(cnt == n-1){ //一棵树有n-1条边 
			break;  //如果小于n-1，则生成树不存在 
		}
	} 
	if(cnt < n-1){ 
		cout<<"生成树不存在"; 
		return;  //如果小于n-1，则生成树不存在 
	}
	
} 
int main()
{
	while(cin>>n>>m){
		Init();
		int x,y,len;
		for(int i = 0; i < m; i++){
			cin>>G[i].x>>G[i].y>>G[i].w;
		}
		Kruskal();
		cout<<ans<<endl<<num<<endl;
		for(int i = 0; i < num; i++){
			int t = Num[i];
			cout<<G[t].x<<" "<<G[t].y<<endl;
		}
	}
	return 0;
}