BST、AVL、RBTree 一脉相承

原创 已于 2025-10-12 22:29:22 修改 · 549 阅读 · 15 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #算法

于 2025-10-11 18:15:10 首次发布

1. BST (Binary Search Tree)

  • 二叉搜索树，顾名思义，它是一种二叉树，并且可以用来进行搜索

1.1 特征

  1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值
  2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件1

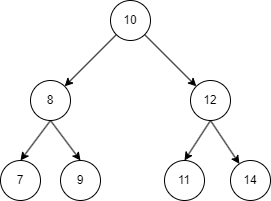
1.2 举例

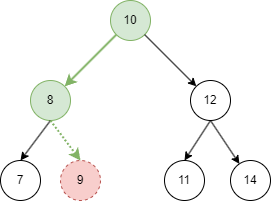
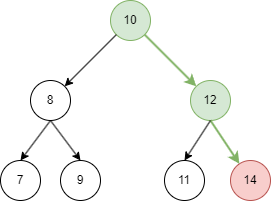
  • 在这里插入图片描述

1.3 查找

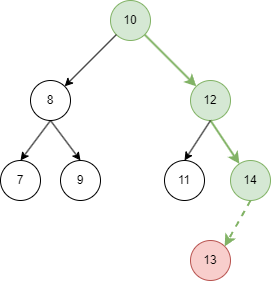
  • 在这里插入图片描述

1.4 插入

  • 在这里插入图片描述

1.5 删除

在这里插入图片描述

2. 平衡二叉树、AVL

  • AVL是平衡二叉树的一种，是一种高度平衡的二叉树，是最早被发明的平衡二叉树
  • 还有Splay Tree、Treap等
  • 大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们提出的平衡二叉树的概念，为了纪念他们，将平衡二叉树称为 AVL树。

2.1 特点

  • 要么是空树
  • 要么左右子树的高度之差的绝对值不超过1

2.2 平衡因子

  • 左子树的高度减去右子树的高度，空节点的平衡因子为0
  • 1、0、-1都认为是平衡的

2.3 旋转

为了维持树的平衡，最重要的操作是对树进行旋转操作，旋转后保持有序和平衡。根据树的形状的不同分为左旋、右旋、先左旋再右旋、先右旋再左旋，下面我们依次进行讨论

2.3.1 LL型

在这里插入图片描述

2.3.2 RR型

在这里插入图片描述

2.3.3 LR型

在这里插入图片描述

2.3.4 RL型

在这里插入图片描述

2.4 分析

  • 旋转的核心就是将中间值放在合适的父节点上，上述的例子就是将6放在父节点上。
  • LR型是先转为LL型，将数字6放在中间位置
  • RL型是先转为RR型，将数字6放在中间位置
  • RR型和LL型的可视化顺序和大小顺序是一致的，可以直接进行旋转

3. 红黑树

  • 继承于二叉搜索树
  • 红黑树是一种不大严格的平衡树(AVL树为了平衡做了太多的旋转)

3.1 特点

  1. 每个节点非红即黑
  2. 根节点是黑的
  3. NIL节点(空叶子节点)为黑色
  4. 红色节点的子节点为黑色
  5. 对于任意节点而言,其到叶子点树NIL指针的每条路径都包含相同数目的黑节点.

3.1.1 理解

  • 红红不能相邻，黑黑可以相邻
  • 有一个不可见的虚拟空节点，颜色为黑，在统计特点5的时候需要考虑在内
  • 新节点默认是红色，如果是黑色，就会影响到特点5
  • 最短路径一定是：全部都是黑色；最长路径为红黑相间

3.1.2 术语

  • 黑黑：两个相邻的黑色节点

  • 红红：两个相邻的红色节点(实际上不会出现)

  • 黑高：节点到叶子节点路途中黑色节点的个数

    添加节点相对比较简单，我们先说添加节点，再说删除节点。

3.3 添加节点

  • 如果是根结点，则为黑色，其他节点默认为红色
  • 如果父节点为黑色，则直接插入即可
  • 如果父节点为红色，则分为以下两种情况

3.3.1 父节点为红，叔节点为红色

  • 因为红色节点的子节点为黑，所以祖先节点一定是黑色节点
  • 因为插入的新节点为红色，出现了非法的红红，这个时候将祖先节点标记为红，父节点和叔节点标记为黑
  • 结果就是增加了一个黑高，导致黑高不一致，将祖先节点作为当前节点沿路径向上进行递归调整
  • 在这里插入图片描述

3.3.2 父节点为红，叔节点为黑

  • 按照LL、LR、RR、RL等四种类型进行旋转，LR转换为LL，RL转换为RR，最终的形状为LL或者RR

  • 父节点变黑，父节点的父节点变红，然后对LL右旋或者对RR左旋后

  • 最终结果是：将相邻的两个红色节点拆开到另一侧，两侧都维持黑高不变，不需要递归

  • LL
    在这里插入图片描述

  • RR
    在这里插入图片描述

  • LR
    在这里插入图片描述

  • RL
    在这里插入图片描述

3.2 删除节点

  • 删除节点的时候如果是叶子节点就执行删除操作，否则需要寻找临近节点替换后再进行删除操作
  • 删除过程中涉及到向上追溯，需要使用栈来记录最终删除节点的路径

3.2.1 目标节点为红色

  • 直接删除即可
  • 因为红色节点一定是空节点
    • 首先它不可能是有红色子节点，红红不能相邻
    • 因为最多有一边有子节点（否则就要继续查找），所以它一定没有黑色子节点，否则两侧的黑高不相同

3.2.2 目标节点为黑色且有孩子节点

  • 子节点一定是红色，否则两侧的黑高不相同
  • 将目标节点删除后，将子节点向上移动，然后改颜色为黑，保持黑高稳定

3.2.3 目标节点为黑色且有无孩子节点(这个最麻烦)

  • 这种情况下，一定有兄弟节点，否则父节点的两侧两侧黑高不相同
  • 之所以考虑兄弟节点，是为了最低成本的保持两侧黑高相同，减少递归次数

3.2.3.1 兄弟节点为黑色

  1. 目标节点是其父节点的右节点，兄弟节点的左节点为红色

    • 属于LL型, 执行右旋，最后直接删除节点
    • 兄弟节点的左节点变黑，维持兄弟节点的黑高
    • 兄弟节点成为父节点，颜色设置为原父亲节点的颜色
    • 原父节点设置为黑色，保持右侧的黑高不变
    • 在这里插入图片描述

  2. 目标节点是其父节点的右节点，兄弟节点的右节点为红色

    • 属于LR型，需要调整为LL型，然后右旋,最后直接删除节点
    • 兄弟节点的右节点颜色转为父节点的颜色(因为最终它会变为父节点)
    • 父节点的颜色变为黑色，因为它会被旋转到右侧，来维持右侧的黑高不变
    • 在这里插入图片描述

  3. 目标节点是其父节点的右节点,兄弟节点无子节点(兄弟节点一定为黑)

    • 将兄弟节点设置为红色，即两侧都同时减去一个黑色节点
    • 如果其父节点刚好为红色，可以立即变黑，保持黑高不变，就可以返回
    • 但是如果父节点刚好黑色，将目标节点删除后向上递归，将父节点转为目标节点进行调整符合红黑树规则

  4. 目标节点是其父节点的左节点,兄弟节点的右节点为红色

    • 属于RR型，执行左旋，最后直接删除目标节点
    • 兄弟节点的右节点变黑，维持兄弟节点的黑高
    • 兄弟节点成为父节点，颜色设置为原父亲节点的颜色
    • 原父节点设置为黑色，保持右侧的黑高不变
    • 在这里插入图片描述

  5. 目标节点是其父节点的左节点,兄弟节点的左节点为红色

    • 属于RL型，调整为RR型，然后左旋,最后直接删除节点
    • 兄弟节点的左节点颜色转为父节点的颜色(因为最终它会变为父节点)
    • 父节点的颜色变为黑色，因为它会被旋转到右侧，来维持右侧的黑高不变
    • 在这里插入图片描述

  6. 目标节点是其父节点的左节点,兄弟节点无子节点(兄弟节点一定为黑)

    • 将兄弟节点设置为红色，即两侧都同时减去一个黑色节点
    • 如果其父节点刚好为红色，可以立即变黑，保持黑高不变，就可以返回
    • 但是如果父节点刚好黑色，将目标节点删除后向上递归，将父节点转为目标节点进行调整符合红黑树规则

3.2.3.2 兄弟节点为红色

  • 这种情形不能直接进行处理，需要转换形态

  1. 目标节点是其父节点的左节点

    • 兄弟节点与父节点互换颜色，即兄弟变为黑色，父亲变为红色
    • 执行左旋
    • 如图所示，旋转后黑高保持不变，继续对D执行删除操作
    • 在这里插入图片描述

  2. 目标节点是其父节点的右节点

    • 兄弟节点与父节点互换颜色，即兄弟变为黑色，父亲变为红色
    • 执行右旋
    • 如图所示，旋转后黑高保持不变，继续对D执行删除操作
    • 在这里插入图片描述

引用

微信公众号为「吹风的坚果」，欢迎关注，定期更新优质的计算机文章。
BST与AVL
weixin_42178281的博客
11-23 1312
树形结构的实际应用 介绍两种树形结构的实际应用，BST和AVL可能相对比较重要，单独放在这里，其实哈夫曼树，堆排序都算树形结构的实际应用 1.BST二叉排序树(左小右大的树) 1.1二叉排序树需求 需求分析： 给你一个数列 { 7, 3, 10, 12, 5, 1, 9 } ，要求能够高效的完成对数据的查询和添加。 解决方案： 1.使用数组 1).数组未排序， 优点：直接在数组尾添加，速度快。 缺点：查找速度慢 2).数组排序，优点：可以使用二分查找，查找速度快，缺点：为了保证数组有序，在添加新数据时，找到
BST和AVL ISSN链接方法改进的算法分析-研究论文
05-19
搜索是计算机中重要且核心的任务。... 本文首先对单独的链接方法进行了额外的分析，并采用了升级方法，即与平衡二叉树（如BST和AVL）链接。 还提供了一些算法来帮助实现改进单独链接的性能并减少搜索元素时的搜索时间。
BST AVL RBTree
varyall的专栏
11-03 625
1、平衡二叉树存意义就是，为了减少搜索时候 ，树的高度太高，搜索效率低下的问题。 2、二叉树最好的情况就是，平衡二叉树O(log2n)，最差的情况就是线性O(n). 3、
BST和RBtree
weixin_34419326的博客
02-19 128
讨论怎么用随机化的方法，使得二叉搜索树在大部分情况下都能保持平衡？1、排序 将数组构建为二叉搜索树，在进行中序遍历，就可顺序输出； BST的时间复杂度为：O(nlogn)；最坏情况：O(n^2)；BST与快速排序的算法思想极为相似；2、随机化BST (1)、随机、均匀地打乱数组的序列； (2)、BST排序； 随机化BST树，排序的算法时间复杂度：O(nlogn)；...
【数据结构】浅谈BST、AVL树、红黑树、B树、B+树
weixin_43868754的博客
03-26 586
面试中，各种数据结构中对于"树"的考查十分普遍，刚开始复习，往往被各种树弄的一头雾水。本文主要对BST、AVL、红黑树、B树、B+树作剖析。 一、概述 BST：二叉搜索树 二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树： （1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值； （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值； （3）左、右子树也分别为二叉排序树； ...
树形结构查找（BST、AVL树、RBT）
kusunoki的博客
08-09 1467
对于二叉排序树（BST）、平衡二叉树（AVL树）以及红黑树（RBT），要了解它们的概念、性质和相关操作等。
BST AVL 红黑树 B B+树
wangprince2017
08-31 213
二叉搜索树(BST) 简明BST递归定义(Knuth Donald)： 对于任意一个节点均满足： 1. 所有位于左子树的节点值均比该节点值小 2. 所有位于右子树的节点值均大于等于该节点值 3. 所有左子树和右子树也必须是BST AVL 简明AVL定义(Knuth Donald)： 对于任意一个节点均满足： 1. 左子树和右子树的高度差小于等于1 红黑树 简明RBTREE定义(...
BSTree，AVLTree，RBTree。
qq_37442823的博客
07-11 190
BSTree BST存在的主要问题是，数在插入的时候会导致树倾斜，不同的插入顺序会导致树的高度不一样，而树的高度直接的影响了树的查找效率。理想的高度是logN，最坏的情况是所有的节点都在一条斜线上，这样的树的高度为N。 (1) 查找代价： 任何一个数据的查找过程都需要从根结点出发，沿某一个路径朝叶子结点前进。因此查找中数据比较次数与树的形态密切相关。 当树中每个结点左右子树高度大致相同时，树高为logN。则平均查找长度与logN成正比，查找的平均时间复杂度在O(logN)数量级上。 当先后插入的关键字有序
BST树和AVL树
m0_56799642的博客
07-09 398
二叉搜索树（BST）是一种特殊的二叉树，每个顶点最多可以有两个子节点。这种结构遵循BST属性，规定给定顶点的左子树中的每个顶点的值必须小于给定顶点的值，右子树中的每个顶点的值必须大于给定顶点的值。将当前节点的右子节点提升为新的根节点。当前节点成为新根节点的左子节点。新根节点原来的左子节点（如果有的话）成为当前节点的右子节点。将当前节点的左子节点提升为新的根节点。当前节点成为新根节点的右子节点。新根节点原来的右子节点（如果有的话）成为当前节点的左子节点。
BST树与AVL树
2301_80948460的博客
09-17 1221
BST为二叉树左子数所有节点都小于根节点，右子树所有节点大于根节点每个节点的左右子树也是BST可以在O(logN)时间复杂度内查找一个数是否存在int data;AVL树是一颗自平衡的二叉树每个节点都有一个平衡因子 p = Height(leftSon) - Height(RightSon)若每个节点的平衡因子的绝对值均<=1，该树是AVL树int data;int height;
bst.rar_The Tree_avl tree_bst
09-24
BST.rar contains a full binary search tree with the usual associated methods including search and delete. Very useful for storing data and converting into an AVL tree.
(BST24208,BST24108,BST24201,BST24212)CAN总线通讯板卡
03-14
在本章节中，我们将深入探讨BST24108、BST24208、BST24201以及BST24212这几种型号的CAN总线通讯板卡的主要特点及其应用场景。 #### 二、BST24108 — PCI总线8通道CAN通讯卡 **主要特性：** - **PCI总线接口**：...
binary-search-tree:使用 HTML、CSS 和 JS 创建的 BST 和 AVL 平衡
07-24
在给定的项目“binary-search-tree: 使用 HTML、CSS 和 JS 创建的 BST 和 AVL 平衡”中，开发者用前端技术实现了对二叉搜索树的可视化操作。 首先，HTML（超文本标记语言）负责构建页面的基本结构，提供用户界面。...
Rust 练习册 67：自定义集合与数据结构实现
少湖说
11-21 557
本文介绍了在Rust中实现自定义集合数据结构的方法。集合是一种存储唯一元素、支持基本集合运算的数据结构。通过两种实现方式：1) 基于标准库HashSet的简单封装；2) 从零开始使用Vec实现。后者需要手动处理元素唯一性检查，并实现交集、并集、差集等运算。文章展示了如何通过泛型编程和trait约束来构建类型安全的集合实现，帮助深入理解Rust数据结构和集合运算原理。
【C语言&数据结构】二叉树的链式递归
最新发布
yuuki233233的博客
11-22 1008
本文介绍了二叉树的链式存储结构及其实现方法。主要内容包括： 链式二叉树的定义：使用包含数据域和左右指针域的节点结构（二叉链）表示二叉树； 创建方法：通过动态分配内存创建节点并构建二叉树； 遍历算法：详细讲解了前序、中序和后序三种递归遍历方式； 常用操作：实现节点计数、叶子节点计数、树高计算、查找特定节点等基本功能； 销毁方法：采用后序遍历顺序释放节点内存。 文章通过代码示例和图解详细说明了各功能的实现过程，特别强调了递归在二叉树操作中的核心作用。
【数据结构】扩展域并查集
2401_87820834的博客
11-19 858
扩展域并查集的应用
Anyview数据结构第一章（按需自取）
2302_79085918的博客
11-22 504
【代码】Anyview数据结构第一章（按需自取）
数据结构：数组
闲余知道
11-21 340
数据结构：数组
掌握数据结构：BST树、AVL树及表格的C++实现
AVL树、BST树和表table是数据结构中的重要概念，它们在计算机科学中用于存储、组织和管理数据。C++是一种广泛使用的编程语言，尤其在系统软件开发和性能密集型应用中非常受欢迎。在这个文件中，我们将探讨AVL树、BST...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值