二叉树的Morris遍历

不同于通过递归实现的中序遍历，二叉树还存在一种通过循环实现的Morris遍历，，这种遍历方式从结果上来看与中序遍历相同，而由于是用循环代替了递归，空间复杂度会从O(H)（H为二叉树的高度）变为O(1)

线索二叉树

二叉树的Morris遍历，是基于线索二叉树来做的

而线索二叉树，简单来讲，就是将左节点不为空的节点的左子树的最右节点的右节点指向该节点

例如这样一个二叉树

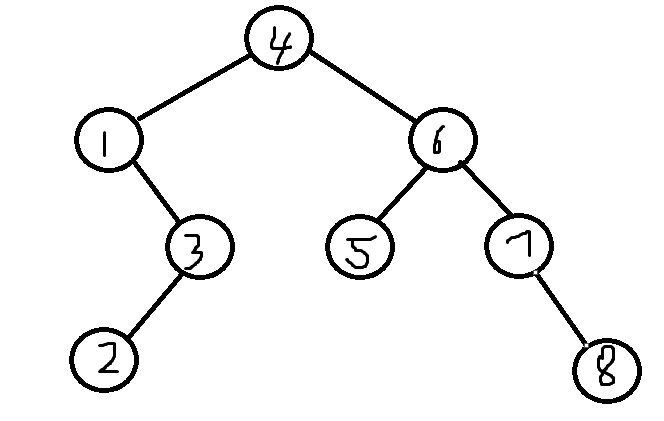
其中 4 的左节点为 1 ，而 1 的最右节点为 3 ，因此我们需要将3的右节点指向 1 （虚线表示）

 

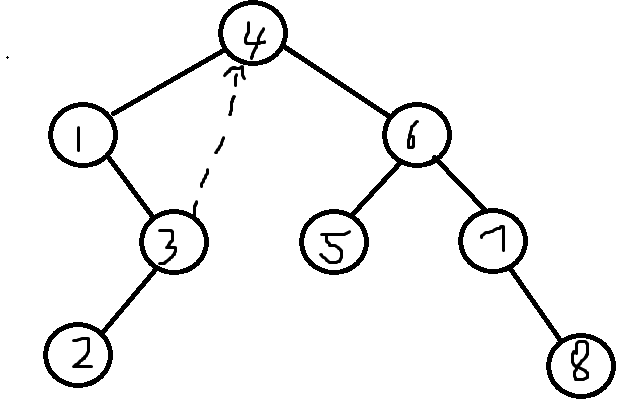
 因此，将该树表示为线索二叉树为

 

---

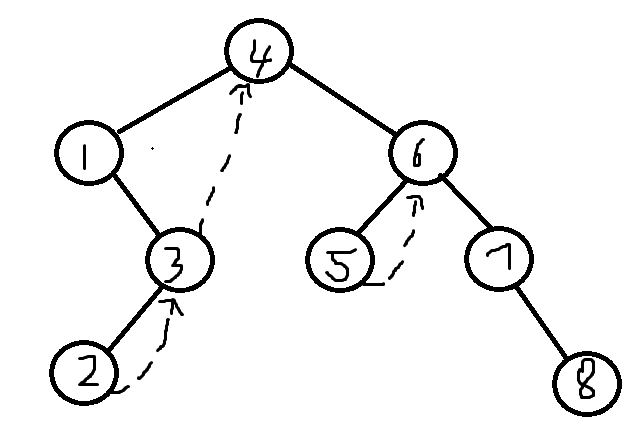
Morris遍历

在中序遍历中，我们的遍历顺序为左节点 - 根节点 - 右节点

首先，想要得到左节点，我们可以直接得到（root=root->left）

而在遍历到左节点后，重点就是如何重新得到根节点，线索二叉树就能够很好的解决这个问题，在遍历完左子树之后，我们一定会处于左子树的最右节点，这时我们就可以通过线索二叉树来重新回到根节点

因此，转换为代码，我们只需要在遍历每个节点时判断是否存在左子树，若存在左子树，则去构建该位置的线索二叉树，并向左遍历， 而若是不存在左子树，则向右遍历

struct TreeNode
{
	int val;
	TreeNode* left = nullptr;
	TreeNode* right = nullptr;
	TreeNode(int v)
		:val(v)
	{}
};

void Morris(TreeNode* root)
{
	while (root)
	{
		if (root->left)
		{
			TreeNode* right_left = root->left;
			while (right_left->right&& right_left != root)
				right_left = right_left->right;
			right_left->right = root;
			root = root->left;
		}
		else
		{
			cout << root->val << "->";
			root = root->right;

		}
	}
	cout << "nullptr";
}

int main()
{
	TreeNode* n1 = new TreeNode(1);
	TreeNode* n3 = new TreeNode(3);
	n3->left = new TreeNode(2);
	n1->right = n3;
	TreeNode* n7 = new TreeNode(7);
	n7->right = new TreeNode(8);
	TreeNode* n6 = new TreeNode(6);
	n6->right = n7;
	n6->left = new TreeNode(5);
	TreeNode* n4 = new TreeNode(4);
	n4->left = n1;
	n4->right = n6;
	Morris(n4);
	return 0;
}

这样看貌似是没有问题的，但是我们要注意，在根节点向后遍历到左子树的最右节点时，下一个遍历的节点会重新根节点，这时，我们已经构建过该节点位置的线索二叉树了，因此这时我们需要之后直接遍历其右节点，因此我们需要对左子树存在的情况做一些处理

void Morris(TreeNode* root)
{
	while (root)
	{
		if (root->left)
		{
			TreeNode* right_left = root->left;
			while (right_left->right&& right_left != root)
				right_left = right_left->right;
			if (right_left != root)
			{
				right_left->right = root;
				root = root->left;
			}
			else
			{
				cout << root->val << "->";
				root = root->right;
			}
		}
		else
		{
			cout << root->val << "->";
			root = root->right;

		}
	}
	cout << "nullptr";
}

这样就不会出现问题了

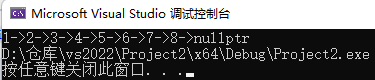
 同时，为了保证二叉树保持原本的模样，我们可以在第二次遍历到根节点时删除构建的线索二叉树

void Morris(TreeNode* root)
{
	while (root)
	{
		if (root->left)
		{
			TreeNode* right_left = root->left;
			while (right_left->right&& right_left != root)
				right_left = right_left->right;
			if (right_left != root)
			{
				right_left->right = root;
				root = root->left;
			}
			else
			{
				right_left->right = nullptr;
				cout << root->val << "->";
				root = root->right;
			}
		}
		else
		{
			cout << root->val << "->";
			root = root->right;

		}
	}
	cout << "nullptr";
}

 

99. 恢复二叉搜索树 - 力扣（Leetcode）

这道题就是运用的Morris遍历实现的空间复杂度为O(1)的算法