SDNU ACM-ICPC 2019 Training Weekly Contest 1（补题）

最新推荐文章于 2020-01-09 12:58:49 发布

原创最新推荐文章于 2020-01-09 12:58:49 发布 · 264 阅读

0 ·

CC 4.0 BY-SA版权

SDNU 专栏收录该内容

4 篇文章

订阅专栏

本文深入探讨了多项比赛编程题目，包括组合数论、数组处理、字符串操作、区间覆盖等，分享了解题思路与高效算法，如快速求解、动态规划、深度优先搜索等，旨在提升参赛者编程能力和比赛策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

代码能力还是欠佳，并伴有主观主义，比赛中把一个水题，看做超难题并把队友的思路给扯远了。。。汗颜。

总结一下这次比赛的题目，一些简单题，只贴简单解释和代码。

A题Concatenated Multiples

题意分析：给一个数组，两两组合，找出 % k 可为 0 的组合的数目。

题目分析：n的数目为2 * 10e5, 如果打暴力的话，一定会超时T掉，然后我们可以考虑下，如何降低时间复杂度呢。

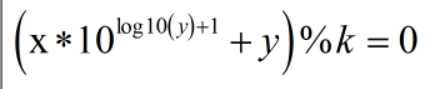
推导得

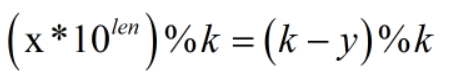
然后我们可以预处理左侧，然后找到符合右边情况的数目，但需要排除本身符合该式的情况。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200010;

int n, k, a[maxn];
map <long long, long long> dp[20]; // map 记录， 因为数组的缘由可能会超long long
int main()
{
    while(scanf("%d%d", &n, &k) != EOF)
    {
        for(int i = 0; i <= 15; i++) dp[i].clear(); // 注意清空

        for(int i = 0; i < n; i++)
        {
            scanf("%d", &a[i]);
            long long x = a[i];
            for(int j = 1; j <= 10; j++)
            {
                x = (x * 10) % k;
                dp[j][x]++; // 预处理 长度1 - 10.
            }
        }
        long long ans = 0;
        for(int i = 0; i < n; i++)
        {
            int len = log10(a[i]) + 1;
            ans += dp[len][(k - a[i] % k) % k];
            long long x = 1;
            for(int j = 1; j <= len; j++) x = (x * 10) % k;
            if(((a[i] * x) % k + a[i] % k) % k == 0) ans--;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

B题Creating the Contest

题意：给定的数组，由小到大排列，然后找出满足aij+1≤aij⋅2的情况。

方法，暴力解决。

#include<bits/stdc++.h>
using namespace std;

int n, d, s, re = 0;
int main()
{

    while(scanf("%d", &n) != EOF)
    {
        int max1 = 0; s = 0, re = 0;
        for(int i = 0; i < n; i++)
        {
            scanf("%d", &d);
            if(d <= 2 * re)
                s++;
            else
            {

                max1 = max(s, max1);
                s = 0;
            }
            re = d;
        }
        max1 = max(s, max1);
        printf("%d\n", max1 + 1);
    }
    return 0;
}

C题Inventory

题意：最小的变换次数，将给定的n个数，都安置在1 - n范围内。

题意分析：开三个数组，一个存给定的n个数，一个有存重复的位置，一个存1 - n还没有使用过的数。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;

int n, a[maxn], num[maxn], s, re[maxn];
bool b[maxn];
int main()
{
    while(scanf("%d", &n) != EOF)
    {
        memset(b, 0, sizeof(b));
        s = 0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &a[i]);
            if(b[a[i]] || a[i] > n)
            {
                num[++s] = i;
            }
            b[a[i]] = 1;
        }
        int s = 0;
        for(int i = 1; i <= n; i++)
        {
            if(!b[i])
                re[++s] = i;
        }
        for(int i = 1; i <= s; i++) a[num[i]] = re[i];
        for(int i = 1; i < n; i++) printf("%d ", a[i]);
        printf("%d\n", a[n]);

    }
    return 0;
}

D题Many Equal Substrings

题意分析：给出1个字符串，然后通过增加尽量少长度来达到k个给出的字符串。

题目分析：可以用substr函数来切出，后面的子串和前面的子串。注意顺序，无论是后面还是前

面顺序都为从前往后。

#include<bits/stdc++.h>
using namespace std;

int n, k;
string t, s, str;
int main()
{
    while(scanf("%d%d", &n, &k) != EOF)
    {
        int re = 0;
        cin >> t;
        s = t; str = "";
        int len = s.size();
        len -= 1;
        for(int i = 1; i < n; i++)
        {
//            cout<<s.substr(0, i)<<endl;
//            cout<<s.substr(n - i, i)<<endl;
            if(s.substr(0, i) == s.substr(n - i, i))
                re = i;
//            cout<<"re = "<<re<<endl;
        }
        for(int i = re; i < n; i++)
            str += t[i];
        cout << t;
        for(int i = 0; i < k - 1; i++)
            cout<<str;
        cout<<endl;
    }
    return 0;
}

E题Maximal Intersection

题意分析：没错，这就是我误导队友的那道题，给定n 个区间，问删除一个区间，使重合的范围达到最大，可以开数组，来记录区间和2个分别记录区间左右位置的数组。

注意点：

1. 区间的重合范围右端点的最小值 - 左端点的最大值。

2.如何模拟删区间操作，因为只是删除一个区间，因而，是否为我们可以判断查找到的区间是否为右端点的最小值，左端点的最大值，在进行偏移即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 300010;

pair <int, int> P[maxn];
int n, a[maxn], b[maxn];
int main()
{
    while(scanf("%d", &n) != EOF)
    {
        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));
        for(int i = 1; i <= n; i++)
        {
            scanf("%d%d", &P[i].first, &P[i].second);
            a[i] = P[i].first; b[i] = P[i].second;
        }
        sort(a + 1, a + n + 1);
        sort(b + 1, b + n + 1);

        int max1 = 0;
        for(int i = 1; i <= n; i++)
        {
            int m1 = a[n], m2 = b[1];
            if(P[i].first == m1) m1 = a[n - 1];
            if(P[i].second == m2) m2 = b[2];
            max1 = max(m2 - m1, max1);
        }
        printf("%d\n", max1);
    }
    return 0;
}

F题Multicolored Markers

题意分析：就是给大小为 a，b 的两个不同的正方形面积。

要求：1. 组成的面积为矩形。

2.至少其中一个为矩形。

3.求他们组成的最小周长

4.相同面积正方形边长小。

题目分析：要满足上述条件，我们需要用一个来填补另一个来构成

#include<bits/stdc++.h>
using namespace std;

long long a, b, re, r;
int main()
{
    while(scanf("%lld%lld", &a, &b) != EOF)
    {
        long long sum = a + b;
        int s1 = sqrt(a);
        int s2 = sqrt(b);
        int len = sqrt(sum);
        long long m = sum;
        for(int i = 1; i <= len; i++)
        {
            if(s1 >= i && a % i == 0) m = min(m, a / i); // 找出长边的值，不断居入中间求数偏正方形的解
            if(s2 >= i && b % i == 0) m = min(m, b / i);
            if(sum % i == 0)
            {
                long long c2 = sum / i;
                if(c2 >= m) r = (c2 + i) * 2;
            }
        }
        printf("%lld\n", r);
    }
    return 0;
}

J题Tree with Small Distances

搜树，DFS递归搜索，然后找到距离大于2的连根，将他的父亲距离设为1，他的距离为2，父亲的父亲也为2.

注意点：

1.连的连边最小。

2.连他的父亲，比直接连叶子结点用的边数少。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200010;

int n, dis[maxn], ans;
vector <int> G[maxn];
void dfs(int a, int fa, int cnt)
{
    dis[a] = cnt;
    int l = G[a].size();
    int flag = 0;
    for(int i = 0; i < l; i++)
    {
        if(G[a][i] == fa) continue;
        dfs(G[a][i], a, cnt + 1);
        if(dis[G[a][i]] > 2)
        {
            flag = 1;
            dis[a] = 1;
            dis[fa] = 2;
        }
    }
    ans += flag;
}
int main()
{
    while(scanf("%d", &n) != EOF)
    {
        ans = 0;
        for(int i = 0; i <= n; i++) G[i].clear(), dis[i] = 0;
        for(int i = 1; i < n; i++)
        {
            int a, b;
            scanf("%d%d", &a, &b);
            G[a].push_back(b);
            G[b].push_back(a);
        }
//        cout<<"---------"<<endl;
        dfs(1, 1, 0);
        printf("%d\n", ans);
    }
    return 0;
}