LeetCode(61)UniquePath1

题目如下:

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Above is a 3 x 7 grid. How many possible unique paths are there?

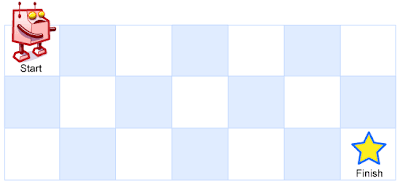
Note: m and n will be at most 100.

分析如下：

目前知道的三种解法，动态规划，排列组合，递归。
第一种，动态规划，比较好想。对于任意一点(x,y)，要么是从(x,y)的左相邻点(x,y-1)过来，要么是从(x,y)的上相邻点(x-1,y)过来。如果用f(x,y)来表示robot走到点(x,y)时的走法，那么f(x,y)=f(x-1,y)+f(x,y-1)。其中，base条件是。当(x,y)位于最上面一行或者最左边一列时，由于robot要么向右走要么向下走，显然只能有1种走法，即f(x,y)=1 if(x==1 or y==0)。这个做法的时间复杂度为O(m,n)，空间复杂度为O(m,n)。如果稍微优化一下，空间复杂度是可以降低为O(min(m,n))的。见下面代码。

第二种，排列组合，挺巧妙的，正好在Cracking the Code Interview书中看到了这种解法。robot从第(1,1)点走到了第(m,n)点。它只能向右或者向下，不管它怎么走，它必然向右走了m-1步，向下走了n-1步。一共走了m-1+n-1步。而不同的走法，本质是向右或者向下构成的m-1+n-1长度的序列不同。走法的总数目，本质上是m-1+n-1个总步数中选出m-1个代表向右走的走法的个数，这个问题的另一种表述是，走法的总数目，本质上是m-1+n-1个总步数中选出n-1个代表向下走的走法的个数。这其实正是组合的小性质。

C(a+b, a)=C(a+b, b)
这样题目就转换为了一个数学计算了，求C(m-1+n-1, m-1)。

第三种，递归的做法。
比较耗时间，我用OJ尝试着提交了一下递归的做法，发现超时了。

我的代码:

// version 1 动态规划 bottom-up
class Solution {
public:
    int uniquePaths(int m, int n) {
        int ** arr = new int* [m];
        for(int i=0;i<m;i++)
            arr[i]=new int[n];
        for(int i=0;i<m;i++)
            arr[i][0]=1;
        for(int i=0;i<n;i++)
            arr[0][i]=1;
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                arr[i][j]=arr[i-1][j]+arr[i][j-1];
            }
        }
        return arr[m-1][n-1];
    }
};

其实不需要用m*n那么大的矩阵，只需要O(min(m,n))大小的一个一维数组就可以了，这样能把动态规划的空间复杂度再优化一下。

// version 2 动态规划 bottom-up 空间复杂度由O(m*n)变化为O(min(m,n));
class Solution {
public:
    int uniquePaths(int m, int n) {
        int s=(m<n)?m:n;
        int l=(m>n)?m:n;
        int * arr= new int [s];
        for(int j=0;j<s;j++)
            arr[j]=1;
        for(int i=1;i<l;i++){
            for(int j=1;j<s;j++){
                arr[j]+=arr[j-1];
            }
        }
        return arr[s-1];
    }
};

// version 3 组合数学角度求从m-1+n-1个数种选出m-1个数的组合的数目,即C(m-1+n-1, m-1)的数目。
class Solution {
public:
    unsigned long long  get_factorial(unsigned long long k){ //计算阶乘
        if(k==0)
            return 1;
        else
            return k*get_factorial(k-1);
    }
    
    int uniquePaths(int m, int n) {
        unsigned long long b=0; //防止溢出，用unsigned long long
        unsigned long long c=0;
        if(m<n){ //从m-1和n-1中选出一个较小的数，节省计算时间。因为C(m+n, n)和C(m+n, m)计算结果相等，所以可以这么简化。
            b=m-1;
            c=n-1;
        }else{
            b=n-1;
            c=m-1;
        }
        unsigned long long res=1;
        unsigned long long keep_b=b;
        while(b>0){
            res*=(b+c);
            b--;
        }
        res=res/get_factorial(keep_b);
        return (int)res;
    }

};

// 提交时发现超时了。
class Solution {
public:
    int _uniquePaths4(int r, int c, int m, int n) {
        if(r==m-1&&c==n-1) //到达目的地，说明发掘了一条可行路径。
            return 1;
        if(r>=m||c>=n) ////这行不能少，否则递归没有终止条件，无限运行下去直到爆栈。
             return 0;
        return _uniquePaths4(r+1, c,m,n)+_uniquePaths4(r, c+1,m,n);
    }
    int uniquePaths(int m, int n) {
        return _uniquePaths4(0,0, m, n);
    }
};

update: 2014-11-09

使用排列组合的方法来做。和上面的排列组合方法思路基本一致。代码更简洁。

class Solution {
private:
    long long cal_factorial(long a, long start = 1) {
        long long res= 1;
        while (a >= start) {
            res *= a;    
            a--;
        }
        return res;
    }
public:
    int uniquePaths(int m, int n) {
        int max_mn = m>n?m:n; //尽可能使得乘积较小，防止溢出
        long long a = cal_factorial(m + n - 2, max_mn);
        long long b = cal_factorial(m + n - 2 - max_mn + 1);
        long long result = a/b;
        return result;    
}
};