codeforces 925 D

Divisible Pairs

题面翻译

你有两个整数 $x,y$ 和一个长为 $n$ 的数组 $a$。

你需要求出有多少个正整数对 $(i,j)$ 满足：

• 1 <= i , j <= n
• $a_i+a_j$ 可被 $x$ 整除
• $a_i-a_j$ 可被 $y$ 整除

$t$ 组数据，$1\le t\le 10^4,1\le n\le 2\times 10^5,\sum n\le 2\times 10^5,1\le a_i,x,y\le 10^9$。

样例 #1

样例输入 #1

7
6 5 2
1 2 7 4 9 6
7 9 5
1 10 15 3 8 12 15
9 4 10
14 10 2 2 11 11 13 5 6
9 5 6
10 7 6 7 9 7 7 10 10
9 6 2
4 9 7 1 2 2 13 3 15
9 2 3
14 6 1 15 12 15 8 2 15
10 5 7
13 3 3 2 12 11 3 7 13 14

样例输出 #1

2
0
1
3
5
7
0

对于求对数的问题思考方法，首先是要看一看数据范围是2e5 ，那么肯定有一些数能用相同的方式表示出来，因为不可能挨个配对，否则就会超时，由于第二三条可以得出来，ai % y == aj % y, ((ai % x) + (aj % x)) % x = =0 其实就是ai % x + aj % x = = x,
推导过程如下



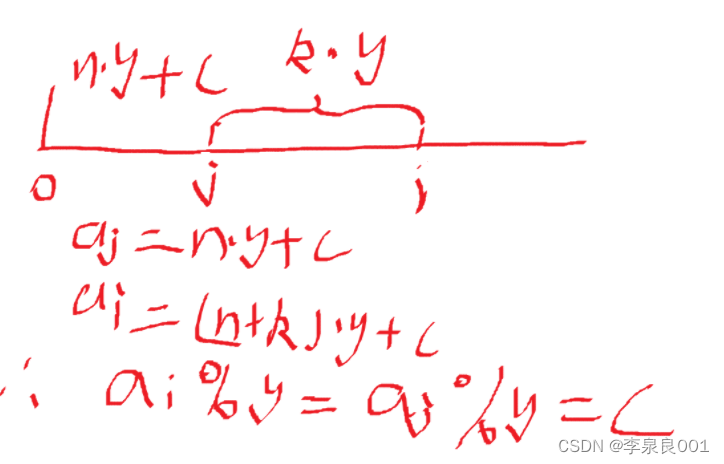
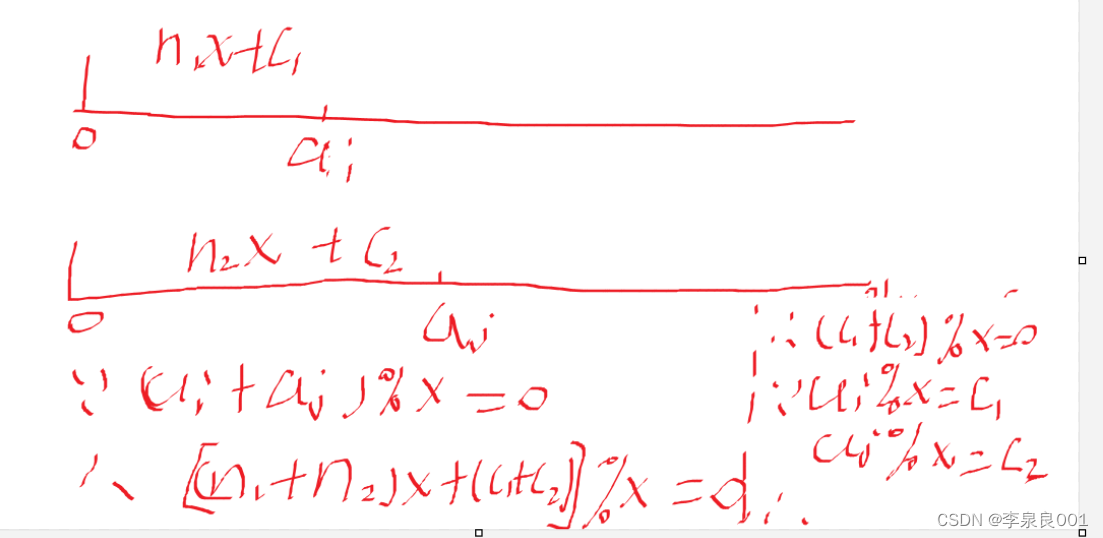
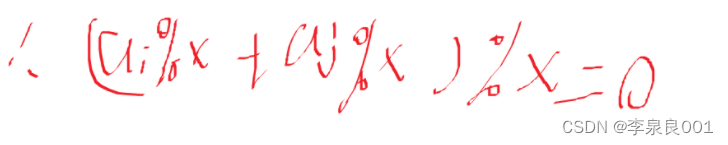
这样之后只需要分两类讨论就可以了
首先，我们值需要讨论x - ai % x 是否ai % x
如果等于那么我们只要记录[x - ai % x][ai % y]， 和[ai % x][ai % y] ,的个数，设为a, b，每个之间都能组成一对，那么就是a * b
否则，因为自己不能与自己一对，所以，是b * (b - 1);
这样你会发现答案不是对的，因为我们记录某一个ai 与 aj 配对的时候也记录了aj 与ai配对，答案多记了一倍，那么最后除以二就是答案。

下面展示一些 内联代码片。

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
 
int main() {
	int t;
	cin >> t;
	while(t --)
	{
		int n ;
		cin >> n;
		int x, y;
		cin >> x >> y;
		vector<int>arr(n);
		map<pair<int ,int >,int>da;
		for(int i = 0;i <  n;i ++)
		{
			cin >> arr[i];
			da[{arr[i]%x,arr[i] % y}]++;
		}
		ll ans = 0;
		for(auto &[a ,b]:da)
		{
			int z1 = x - a.first,z2 = a.second;
			z1 %= x,z2%= y;
			if(a.first != z1)ans += (ll)da[{z1%x,z2 %y}] * b;
			else {
				ans += (ll)b *(b - 1);
			}
		}
		ans /= 2;
		cout << ans << endl;
	}
	return 0;
}