最大似然估计直观理解

目的

由于直接估计类条件概率密度函数很困难。
解决的办法，把估计完全未知的概率密度转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，
极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值。
重要前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。

对于正态分布
1、测量值接近平均
2、测量值围绕均值对称

我们先来看旧的数据分布，这种情况下，分布平均值与实际测量平均值不同。因此，观察到红框里面的数据的可能性很小

因此我们需要找出分布居中的位置

最大似然估计

我们根据分布中心的位置，绘制观测到数据的可能性

我们希望最大化观测可能性的位置，如下图所示

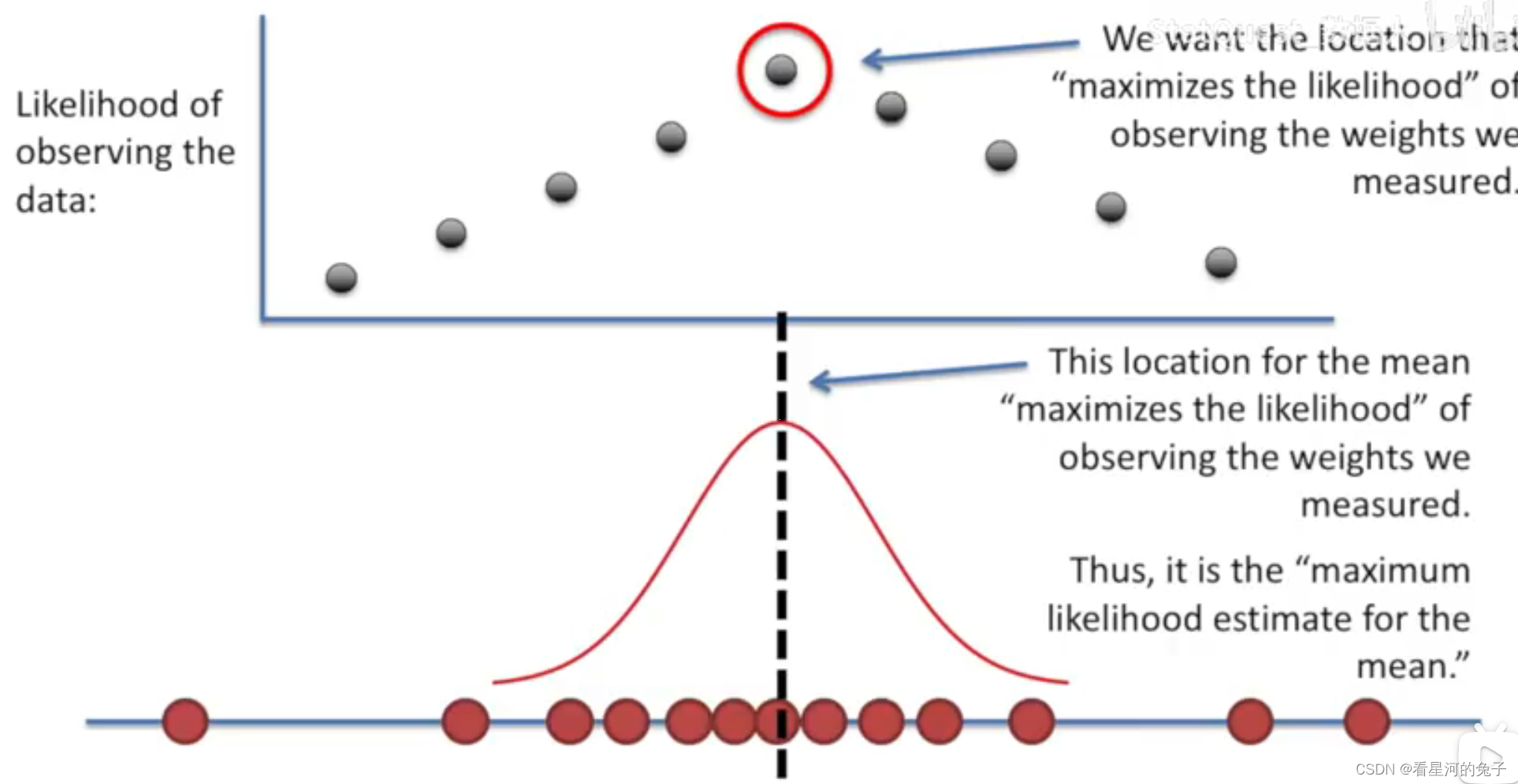
至此，我们已经找出均值的最大似然估计，我们还需要找出标准差的最大似然估计

当某人说他们有对均值，标准差，或其他东西的最大似然估计时，就可以知道他们找到了均值、标准差或其它使观察到事物的可能性最大的值。