python刷题+leetcode(第三部分)

最新推荐文章于 2024-06-16 12:21:53 发布

薛定谔的智能

最新推荐文章于 2024-06-16 12:21:53 发布

阅读量2.4k

点赞数

分类专栏：数据结构与算法

本文链接：https://blog.youkuaiyun.com/fanzonghao/article/details/113052389

版权

数据结构与算法专栏收录该内容

23 篇文章

订阅专栏

200.最大正方形

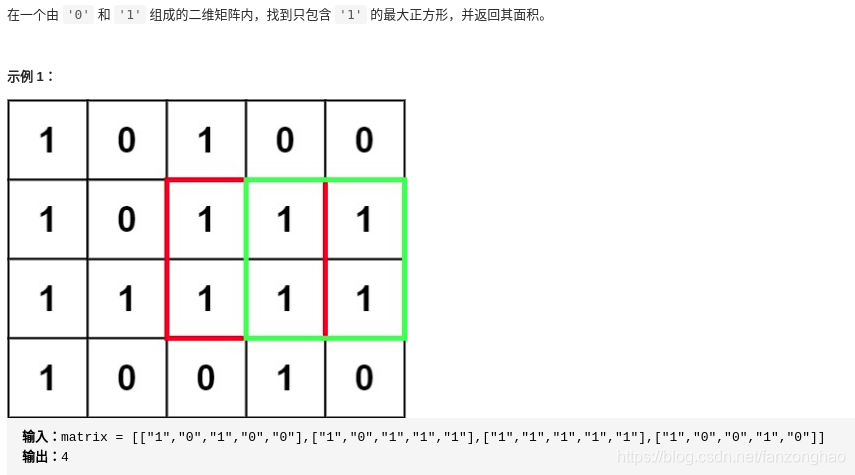
思路:与岛屿，水塘不同的是这个相对要规则得多，而不是求连通域，所以动态规划构造出状态转移方程即可

动态规划　if 0, dp[i][j] =0

if 1, dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1

class Solution:
    def maximalSquare(self, matrix):
        print('==np.array(matrix):\n', np.array(matrix))
        h = len(matrix)
        w = len(matrix[0])
        max_side = 0
        dp = [[0 for j in range(w)] for i in range(h)]
        print('==dp:', np.array(dp))

        for i in range(h):
            for j in range(w):
                if matrix[i][j] == '1' and i>0 and j>0:
                    dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
                    max_side = max(max_side, dp[i][j])
                elif i==0:
                    dp[i][j] = int(matrix[i][j])
                    max_side = max(max_side, dp[i][j])
                elif j==0:
                    dp[i][j] = int(matrix[i][j])
                    max_side = max(max_side, dp[i][j])
                else:
                    pass
        print('==dp:', np.array(dp))
        # print(max_side)
        return max_side**2


matrix = [["1", "0", "1", "0", "0"], ["1", "0", "1", "1", "1"], ["1", "1", "1", "1", "1"], ["1", "0", "0", "1", "0"]]

sol = Solution()
sol.maximalSquare(matrix)

201.统计全为 1 的正方形子矩阵

思路:动态规划　if 0, dp[i][j] =0

if 1, dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1

为１的时候　res自加1,再加上dp[i][j]增加的部分，也可以看成是dp的和

class Solution:
    def countSquares(self, matrix):
        print('==np.array(matrix)\n', np.array(matrix))
        h = len(matrix)
        w = len(matrix[0])
        dp = [[0 for i in range(w)] for j in range(h)]
        print('==np.array(dp):', np.array(dp))
        res = 0
        for i in range(h):
            for j in range(w):
                if matrix[i][j] == 1 and i > 0 and j > 0:
                    res += 1
                    dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
                    res += dp[i][j] - 1  # 减去1代表增加的矩形个数
                elif i==0:
                    dp[i][j] = matrix[i][j]
                    if matrix[i][j] == 1:
                        res+=1
                elif j==0:
                    dp[i][j] = matrix[i][j]
                    if matrix[i][j] == 1:
                        res+=1
                else:
                    pass
        print('==np.array(dp):', np.array(dp))
        print('==after res:', res)
        return res


matrix = [
    [0, 1, 1, 1],
    [1, 1, 1, 1],
    [0, 1, 1, 1]
]
sol = Solution()
sol.countSquares(matrix)

202.平方数之和

思路:双指针左右收缩即可

class Solution:
    def judgeSquareSum(self, c: int) -> bool:
        from math import sqrt
        right = int(sqrt(c))
        left = 0
        while(left <= right):
            sum_ = left**2 + right**2
            if (sum_ == c):
                return True
            elif sum_ > c:
                right -= 1
            else:
                left += 1
        return False

c++实现:

class Solution {
public:
    bool judgeSquareSum(int c) {
        long left = 0, right = sqrt(c);
        while(left <= right){
            long sum_ = left*left + right*right;
            if(sum_ == c){
                return true;
            }
            else if(sum_ > c){
                right--;
            }
            else{
                left++;
            }
        }
        return false;
        
    }
};

203.分发饼干

思路:排序加贪心　先给胃口小的饼干

#思路:排序加贪心 先让胃口小的孩子满足
class Solution:
    def findContentChildren(self, g, s):
        print('==g:', g)
        print('==s:', s)
        g = sorted(g)#孩子
        s = sorted(s)#饼干
        res = 0
        for j in range(len(s)):#遍历饼干　先给胃口小的分配
            if res<len(g):
                if g[res]<=s[j]:
                    res+=1
        print('==res:', res)
        return res

    
g = [1,2]
s = [1,2,3]
# g = [1, 2, 3]
# s = [1, 1]
sol = Solution()
sol.findContentChildren(g, s)

204.三角形最小路径和

思路:动态规划

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        for i in range(1, len(triangle)):
            for j in range(len(triangle[i])):
                if j == 0:
                    triangle[i][j] = triangle[i-1][j] + triangle[i][j]
                elif j == i:
                    triangle[i][j] = triangle[i-1][j-1] + triangle[i][j]
                else:
                    triangle[i][j] = min(triangle[i-1][j-1], triangle[i-1][j]) + triangle[i][j]
        return min(triangle[-1])

c++:

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int h = triangle.size();
        for(int i = 1; i < triangle.size(); i++){
            for(int j = 0; j < triangle[i].size(); j++){
                if(j == 0){
                    triangle[i][j] = triangle[i-1][j] + triangle[i][j];
                }
                else if(j == i){
                    triangle[i][j] = triangle[i-1][j-1] + triangle[i][j];
                }
                else{
                    triangle[i][j] = min(triangle[i-1][j-1], triangle[i-1][j]) + triangle[i][j];
                }
            }
        }
        return *min_element(triangle[h - 1].begin(), triangle[h - 1].end());
    }
};

205.同构字符串

思路:hash　　构造映射关系

class Solution:
    def isIsomorphic(self, s: str, t: str) -> bool:
        if len(s) != len(t):
            return False
        dic = {}
        for i in range(len(s)):
            if s[i] not in dic:#未出现过
                if t[i] in dic.values():#value已经出现过之前构造的dict中了
                    return False
                dic[s[i]] = t[i]
                
            else:#出现过
                 if dic[s[i]]!=t[i]:
                     return False
        return True

# s = "egg"
# t = "add"
s="ab"
t="aa"

sol = Solution()
sol.isIsomorphic(s, t)

206.单词接龙 II

思路:构建图然后bfs

class Solution:
    def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:
        cost = {}
        for word in wordList:
            cost[word] = float("inf")
        cost[beginWord] = 0
        # print('==cost:', cost)
        # neighbors = collections.defaultdict(list)
        neighbors = {}
        ans = []
        #构建图
        for word in wordList:
            for i in range(len(word)):
                key = word[:i] + "*" + word[i + 1:]
                if key not in neighbors:
                    neighbors[key] = []
                    neighbors[key].append(word)
                else:
                    neighbors[key].append(word)
        # print('==neighbors:', neighbors)
        q = collections.deque([[beginWord]])
        # q = [[beginWord]]
        # print('====q:', q)
        #bfs
        while q:
            # path = q.popleft()
            path = q.pop()
            # print('===path:', path)
            cur = path[-1]
            if cur == endWord:
                ans.append(path.copy())
            else:
                for i in range(len(cur)):
                    new_key = cur[:i] + "*" + cur[i + 1:]
                    if new_key not in neighbors:
                        continue
                    for neighbor in neighbors[new_key]:
                        # print('==cost[cur] + 1, cost[neighbor]:', cost[cur] + 1, cost[neighbor])
                        if cost[cur] + 1 <= cost[neighbor]:
                            q.append(path + [neighbor])
                            cost[neighbor] = cost[cur] + 1
        # print('==ans:', ans)
        return ans

208.最后一块石头的重量

思路1:while循环　排序从大到小　一直取前两块石头进行比较


class Solution:
    def lastStoneWeight(self, stones):
        while len(stones)>=2:
            stones = sorted(stones)[::-1]
            if stones[0]==stones[1]:
                stones=stones[2:]
            else:
                stones = [stones[0]-stones[1]]+stones[2:]
        print('===stones:', stones)
        return stones[-1] if len(stones) else 0



stones = [2, 7, 4, 1, 8, 1]
# stones = [2, 2]
sol = Solution()
res= sol.lastStoneWeight(stones)
print('==res:', res)

更简洁写法：

class Solution:
    def lastStoneWeight(self, stones: List[int]) -> int:
        while len(stones) >= 2:
            stones = sorted(stones)
            stones.append(stones.pop() - stones.pop())
        return stones[0]

思路2:堆队列，也称为优先队列



import heapq
class Solution:
    def lastStoneWeight(self, stones):
        h = [-stone for stone in stones]
        heapq.heapify(h)

        print('==h:', h)
        while len(h) > 1:
            a, b = heapq.heappop(h), heapq.heappop(h)
            if a != b:
                heapq.heappush(h, a - b)
            print('==h:', h)
        return -h[0] if h else 0



stones = [2, 7, 4, 1, 8, 1]
# stones = [2, 2]
sol = Solution()
res= sol.lastStoneWeight(stones)
print('==res:', res)

210.无重叠区间


class Solution:
    def eraseOverlapIntervals(self, intervals):

        n = len(intervals)
        if n<=0:
            return 0
        intervals = sorted(intervals, key=lambda x: x[-1])
        print('==intervals:', intervals)
        
        res = [intervals[0]]
        for i in range(1, n):
            if intervals[i][0] >= res[-1][-1]:
                res.append(intervals[i])
        print(res)
        return n - len(res)


# intervals = [[1, 2], [2, 3], [3, 4], [1, 3]]
# intervals = [[1,100],[11,22],[1,11],[2,12]]
intervals = [[0, 2], [1, 3], [2, 4], [3, 5], [4, 6]]
sol = Solution()
sol.eraseOverlapIntervals(intervals)

212.种花问题

思路:判断是否是1或0,1就一种情况,0有两种情况

100 先判断1

01000,要判断i为0时,i+1是否为1,否则说明就是001这种情况


# 100 先判断1
# 01000,要判断i为0时,i+1是否为1,否则说明就是001这种情况
class Solution:
    def canPlaceFlowers(self, flowerbed, n):

        i = 0
        res = 0
        while i<len(flowerbed):
            if flowerbed[i]==1:
                i+=2
            else:
                if i+1<len(flowerbed) and flowerbed[i+1]==1:
                    i+=3
                else:
                    res+=1
                    i+=2

        return True if res>=n else False

# flowerbed = [1,0,0,0,1]
# n = 1

# flowerbed = [1,0,0,0,1]
# n = 2

# flowerbed = [1,0,0,0,0,0,1]
# n = 2
flowerbed = [1,0,0,0,1,0,0]
n = 2
sol = Solution()
res= sol.canPlaceFlowers(flowerbed, n)
print('==res:', res)

216.较大分组的位置

其实就是再求聚类

思路1:动态规划


class Solution:
    def largeGroupPositions(self, s):
        dp = [0] * len(s)
        for i in range(1, len(s)):
            if s[i] == s[i - 1]:
                dp[i] = 1

        dp.append(0)
        print('==dp:', dp)
        index = [j for j in range(len(dp)) if dp[j] == 0]
        print('index:', index)
        res = []
        for k in range(len(index) - 1):
            if index[k + 1] - index[k] >= 3:
                res.append([index[k], index[k + 1] - 1])
        print('=res:', res)
        return res


s = "abbxxxxzzy"
sol = Solution()
sol.largeGroupPositions(s)

思路2:双指针


# 双指针
class Solution:
    def largeGroupPositions(self, s):
        res = []
        left, right = 0, 0
        while left < len(s):
            right = left + 1
            while right < len(s) and s[right] == s[left]:
                right += 1
            if right - left >= 3:
                res.append([left, right - 1])
            # 左指针跑到右指针位置
            left = right
        print('==res:', res)
        return res

s = "abbxxxxzzy"
# s = "abcdddeeeeaabbbcd"
sol = Solution()
sol.largeGroupPositions(s)

217.省份数量

思路：

可以把 n 个城市和它们之间的相连关系看成图， #

城市是图中的节点，相连关系是图中的边，

给定的矩阵isConnected 即为图的邻接矩阵，省份即为图中的连通分量。

利用dfs将一个数组view遍历过的城市置位1。


# dfs
# 可以把 nn 个城市和它们之间的相连关系看成图，
# 城市是图中的节点，相连关系是图中的边，
# 给定的矩阵isConnected 即为图的邻接矩阵，省份即为图中的连通分量。
class Solution:
    def travel(self, isConnected, i, n):
        self.view[i] = 1  # 表示已经遍历过
        for j in range(n):
            if isConnected[i][j] == 1 and not self.view[j]:
                self.travel(isConnected, j, n)

    def findCircleNum(self, isConnected):
        n = len(isConnected)
        self.view = [0] * n
        res = 0
        for i in range(n):
            if self.view[i] != 1:
                res += 1
                self.travel(isConnected, i, n)
        print('==res:', res)
        return res

# isConnected = [[1, 1, 0],
#                [1, 1, 0],
#                [0, 0, 1]]
isConnected = [[1,0,0],
               [0,1,0],
               [0,0,1]]
sol = Solution()
sol.findCircleNum(isConnected)

218.旋转数组

思路1:截断拼接，注意的是一些边界条件需要返回原数组

class Solution:

    def rotate(self, nums: List[int], k: int) -> None:
        if len(nums)<=1 or k==0 or k%len(nums)==0:
            return nums
        n = len(nums)
        k = k%n
        # print(nums[-k:]+nums[:n-k])
        nums[:] = nums[-k:]+nums[:n-k]
        return nums

思路2:先左翻转，在右翻转，在整体翻转


class Solution:

    def reverse(self, i, j, nums):#交换位置的
        while i < j:#
            nums[i], nums[j] = nums[j], nums[i]
            i += 1
            j -= 1

    def rotate(self, nums, k):
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(nums)
        k %= n #有大于n的数
        self.reverse(0, n - k - 1, nums) #左翻
        self.reverse(n - k, n - 1, nums) #右翻
        self.reverse(0, n - 1, nums) #整体翻
        print(nums)
        return nums

# nums = [1,2,3,4,5,6,7]
# k = 3
nums = [1,2,3,4,5,6]
k = 11
sol = Solution()
sol.rotate(nums, k)

219．汇总区间

思路:双指针


class Solution:
    def summaryRanges(self, nums):
        res = []
        left =0
        right = 0
        while right<len(nums):
            right = left+1
            while right<len(nums) and nums[right] - nums[right-1] == 1:
                right+=1
            if right -1>left:
                res.append(str(nums[left]) + "->" + str(nums[right-1]))
            else:
                res.append(str(nums[left]))
            left = right
        print(res)
        return res
nums = [0,1,2,4,5,7]
sol = Solution()
sol.summaryRanges(nums)

220.冗余连接

思路:并查集


#并查集:合并公共节点的,对相邻节点不是公共祖先的进行合并
class Solution:
    def find(self, index):  # 查询
        if self.parent[index] == index:  # 相等就返回
            return index
        else:
            return self.find(self.parent[index])  # 一直递归找到节点index的祖先

    def union(self, i, j):  # 合并
        self.parent[self.find(i)] = self.find(j)

    def findRedundantConnection(self, edges):
        nodesCount = len(edges)
        self.parent = list(range(nodesCount + 1))
        print('==self.parent:', self.parent)

        for node1, node2 in edges:
            print('==node1, node2:', node1, node2)
            if self.find(node1) != self.find(node2):#相邻的节点公共祖先不一样就进行合并
                print('===hahhaha===')
                self.union(node1, node2)
                print('=self.parent:', self.parent)
            else:
                return [node1, node2]

        return []


edges = [[1, 2], [1, 3], [2, 3]]
sol = Solution()
res = sol.findRedundantConnection(edges)
print('=res:', res)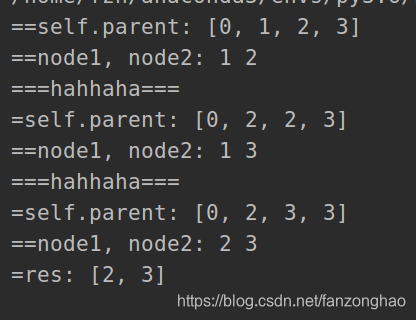

223.可被 5 整除的二进制前缀

思路:二进制移位　在和5求余

class Solution:
    def prefixesDivBy5(self, A: List[int]) -> List[bool]:
        res = [False]*len(A)
        value = 0
        for i in range(len(A)):
            value = (value<<1) + A[i]
            # print(value)
            if value%5==0:
                res[i]=True
        return res

225.移除最多的同行或同列石头

思路1: 其实主要是算连通域的个数,当满足同行或者同列就算联通，
输出的结果就是石头个数减去连通域个数,第一种解法超时


# 其实主要是算连通域的个数,当满足同行或者同列就算联通，
# 输出的结果就是石头个数减去连通域个数
#第一种直接dfs会超时
import numpy as np
class Solution:
    def dfs(self, rect, i, j, h, w):
        if i < 0 or i >= h or j < 0 or j >= w or rect[i][j] != 1:
            return
        rect[i][j] = -1
        for i_ in range(h):
            self.dfs(rect, i_, j, h, w)
        for j_ in range(w):
            self.dfs(rect, i, j_, h, w)

    def removeStones(self, stones):
        n = 10
        rect = [[0 for _ in range(n)] for _ in range(n)]
        print(len(rect))
        for stone in stones:
            rect[stone[0]][stone[-1]] = 1
        print('before np.array(rect):', np.array(rect))
        h, w = n, n
        graphs = 0
        for i in range(h):
            for j in range(w):
                if rect[i][j] == 1:
                    graphs += 1
                    self.dfs(rect, i, j, h, w)
        print('after np.array(rect):', np.array(rect))
        print(graphs)
        return len(stones) - graphs


stones = [[0, 0], [0, 1], [1, 0], [1, 2], [2, 1], [2, 2]]
sol = Solution()
res = sol.removeStones(stones)
print('===res:', res)

思路2:并查集


class Solution:
    # 并查集查找
    def find(self, x):
        if self.parent[x] == x:
            return x
        else:
            return self.find(self.parent[x])
    #合并
    def union(self,i, j):
        self.parent[self.find(i)] = self.find(j)
    def removeStones(self, stones):
        # 因为x,y所属区间为[0,10^4]
        # n = 10001
        n = 10
        self.parent = list(range(2 * n))
        for i, j in stones:
            self.union(i, j + n)
            print('==self.parent:', self.parent)

        # 获取连通区域的根节点
        res = []
        for i, j in stones:
            res.append(self.find(i))
        print('=res:', res)
        return len(stones) - len(set(res))


stones = [[0, 0], [0, 1], [1, 0], [1, 2], [2, 1], [2, 2]]
sol = Solution()
res = sol.removeStones(stones)
print('===res:', res)

226..缀点成线

思路:判断斜率将除换成加


class Solution:
    def checkStraightLine(self, coordinates):
        n = len(coordinates)
        for i in range(1, n-1):
            if (coordinates[i+1][1]-coordinates[i][1])*(coordinates[i][0]-coordinates[i-1][0])=(coordinates[i][1]-coordinates[i-1][1])*(coordinates[i+1][0]-coordinates[i][0]):
                return False
        return True


coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
sol = Solution()
sol.checkStraightLine(coordinates)

227.账户合并

思路:并查集

#思想是搜索每一行的每一个邮箱，如果发现某一行的某个邮箱在之前行出现过，那么把该行的下标和之前行通过并查集来合并，
class Solution(object):
    def find(self, x):
        if x == self.parents[x]:
            return x
        else:
            return self.find(self.parents[x])
    def union(self,i, j):
        self.parents[self.find(i)] = self.find(j)
    def accountsMerge(self, accounts):
        # 用parents维护每一行的父亲节点
        # 如果parents[i] == i, 表示当前节点为根节点
        self.parents = [i for i in range(len(accounts))]
        print('==self.parents:', self.parents)
        dict_ = {}

        # 如果发现某一行的某个邮箱在之前行出现过，那么把该行的index和之前行合并（union）即可
        for i in range(len(accounts)):
            for email in accounts[i][1:]:
                if email in dict_:
                    self.union(dict_[email], i)
                else:
                    dict_[email] = i
        print('===self.parents:', self.parents)
        print('=== dict_:', dict_)
        import collections
        users = collections.defaultdict(set)
        print('==users:', users)
        res = []
        # 1. users：表示每个并查集根节点的行有哪些邮箱
        # 2. 使用set：避免重复元素
        # 3. 使用defaultdict(set)：不用对每个没有出现过的根节点在字典里面做初始化
        for i in range(len(accounts)):
            for account in accounts[i][1:]:
                users[self.find(i)].add(account)
        print('==users:', users)
        # 输出结果的时候注意结果需按照字母顺序排序（虽然题目好像没有说）
        for key, val in users.items():
            res.append([accounts[key][0]] + sorted(list(val)))

        return res


accounts = [["John", "johnsmith@mail.com", "john00@mail.com"],
            ["John", "johnnybravo@mail.com"],
            ["John", "johnsmith@mail.com", "john_newyork@mail.com"],
            ["Mary", "mary@mail.com"]]

# [["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'],
#  ["John", "johnnybravo@mail.com"],
#  ["Mary", "mary@mail.com"]]

sol = Solution()
res= sol.accountsMerge(accounts)
print(res)

228.连接所有点的最小费用

思路1: 其实就是求最小生成树，首先想到的是kruskal 但是时间复杂度较高,超时


# 其实就是求最小生成树:采用kruskal 但是时间复杂度较高,超时
class Solution:
    def minCostConnectPoints(self, points):
        edge_list = []
        nodes = len(points)
        for i in range(nodes):
            for j in range(i):
                dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
                edge_list.append([i, j, dis])
        print('==edge_list:', edge_list)
        edge_list = sorted(edge_list, key=lambda x: x[-1])
        print('==edge_list:', edge_list)
        group = [[i] for i in range(nodes)]
        print('==group:', group)
        res = 0
        for edge in edge_list:
            for i in range(len(group)):
                if edge[0] in group[i]:
                    m = i  # 开始节点
                if edge[1] in group[i]:
                    n = i  # 结束节点
            if m != n:
                # res.append(edge)
                res += edge[-1]
                group[m] = group[m] + group[n]
                group[n] = []
            print(group)
        print('==res:', res)
        return res

points = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
sol = Solution()
sol.minCostConnectPoints(points)

思路2: 其实就是求最小生成树，首先想到的是prim 但是时间复杂度较高,超时


# prim算法 超出时间限制
class Solution:
    def minCostConnectPoints(self, points):
        # edge_list = []
        nodes = len(points)
        Matrix = [[0 for i in range(nodes)] for j in range(nodes)]
        for i in range(nodes):
            for j in range(nodes):
                dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
                # edge_list.append([i, j, dis])
                Matrix[i][j] = dis
        # print('===edge_list:', edge_list)
        print('==Matrix:', Matrix)
        selected_node = [0]
        candidate_node = [i for i in range(1, nodes)]  # 候选节点
        print('==candidate_node:', candidate_node)
        # res = []
        res = 0
        while len(candidate_node):
            begin, end, minweight = 0, 0, float('inf')
            for i in selected_node:
                for j in candidate_node:
                    if Matrix[i][j] < minweight:
                        minweight = Matrix[i][j]
                        begin = i  # 存储开始节点
                        end = j  # 存储终止节点
            # res.append([begin, end, minweight])
            print('==end:', end)
            res += minweight
            selected_node.append(end)  # 找到权重最小的边　加入可选节点
            candidate_node.remove(end)  # 候选节点被找到　进行移除
        print('==res:', res)
        return res


points = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
# points = [[-1000000, -1000000], [1000000, 1000000]]
sol = Solution()
sol.minCostConnectPoints(points)

思路3:并查集


class Solution:
    def find(self, x):
        if self.parents[x] == x:
            return x
        else:
            return self.find(self.parents[x])  # 一直找到帮主

    def union(self, i, j):  # 替换为帮主　站队
        self.parents[self.find(i)] = self.find(j)

    def minCostConnectPoints(self, points):
        costs_list = []
        n = len(points)
        for i in range(n):
            for j in range(i + 1, n):
                dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
                costs_list.append([dis, i, j])
        # print('==costs_list:', costs_list)
        costs_list = sorted(costs_list, key=lambda x: x[0])
        print('==costs_list:', costs_list)

        self.parents = [i for i in range(n)]
        print('==init self.parents:', self.parents)
        res = 0
        for i in range(len(costs_list)):
            dis, x, y = costs_list[i]
            if self.find(x) != self.find(y):
                self.union(x, y)
                print('==x,y:', x, y)
                print('==self.parents:', self.parents)
                res += dis
        print('==res:', res)
        return res


points = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
sol = Solution()
sol.minCostConnectPoints(points)

229.正则表达式匹配

思路:字符串的匹配问题，自然想到用ｄｐ，做成二维矩阵方便进行状态方程的转移

f[i][j]:s的前i个字符和p的前j个字符是否相等
p的第j个字符是字母：p[j]==s[i]时 ,f[i][j]=f[i-1][j-1]
p的第j个字符是字母:p[j]!=s[i]时 ,f[i][j]=False

p的第j个字符是*:s[i]==p[j-1],f[i][j]=f[i-1][j] or f[i][j-2]
p的第j个字符是*:s[i]!=p[j-1],f[i][j]=f[i][j-2]


#f[i][j]:s的前i个字符和p的前j个字符是否相等
#p的第j个字符是字母：p[j]==s[i]时 ,f[i][j]=f[i-1][j-1]
#p的第j个字符是字母:p[j]!=s[i]时 ,f[i][j]=False

#p的第j个字符是*:s[i]==p[j-1],f[i][j]=f[i-1][j] or f[i][j-2]
#p的第j个字符是*:s[i]!=p[j-1],f[i][j]=f[i][j-2]
class Solution:
    def match(self, i, j, s, p):
        if i == 0:
            return False
        if p[j - 1] == '.':
            return True
        return s[i - 1] == p[j - 1]

    def isMatch(self, s, p):
        m, n = len(s), len(p)

        f = [[False] * (n + 1) for _ in range(m + 1)]
        f[0][0] = True
        for i in range(m + 1):
            for j in range(1, n + 1):
                if p[j - 1] == '*':
                    # f[i][j] = f[i][j] or f[i][j - 2]
                    if self.match(i, j - 1, s, p):
                        f[i][j] = f[i - 1][j] or f[i][j-2]
                    else:
                        f[i][j] = f[i][j - 2]
                else:
                    if self.match(i, j, s, p):
                        f[i][j] = f[i - 1][j - 1]
                    else:
                        f[i][j] = False
        print('==f:', f)
        return f[m][n]


s = "aa"
p = "a"
sol = Solution()
sol.isMatch(s, p)

230.最长回文子串

思路:中心枚举，双指针，需要注意的是有上述两种情况，左右指针的索引有两种


class Solution:
    def help(self, left, right, s, n):
        while left >= 0 and right < n:
            if s[left] == s[right]:
                left -= 1
                right += 1
            else:
                break
        temp = s[left+1:right]
        self.res = max(self.res, temp, key=len)

    def longestPalindrome(self, s):
        self.res = s[0]
        n = len(s)
        for i in range(1, n):
            self.help(i-1, i+1, s, n)#针对"babad"
            self.help(i - 1, i, s, n)#针对"cbbd"
        print('==self.res:', self.res)
        return self.res

# s = "babad"
s = "cbbd"
sol = Solution()
sol.longestPalindrome(s)

231.寻找两个正序数组的中位数

思路:双指针，走完剩下的在进行合并


class Solution:
    def findMedianSortedArrays(self, nums1, nums2):
        res = []
        i, j = 0, 0
        m, n = len(nums1), len(nums2)
        while i < m and j < n:
            if nums1[i] < nums2[j]:
                res.append(nums1[i])
                i += 1
            else:
                res.append(nums2[j])
                j += 1
        print('==res:', res)
        print('==i:', i)
        print('==j:', j)
        if i < m:
            res.extend(nums1[i:])
        if j < n:
            res.extend(nums2[j:])
        print('==res:', res)
        if (m+n)%2==0:#偶数
            return (res[(m+n)//2]+res[(m+n)//2-1])/2
        else:#奇数
            return res[(m+n)//2]


# nums1 = [1, 1, 3]
# nums2 = [2]
nums1 = [1,2]
nums2 = [3,4]
sol = Solution()
res = sol.findMedianSortedArrays(nums1, nums2)
print(res)

232.连通网络的操作次数

思路:并查集其实就是求当前的联通量个数减去一个联通量的值,对于n个节点,要给n-1条边才会满足都能连上,采用并查集去做聚类,否则就不满足了


class Solution:
    def find(self, x):
        if x==self.parent[x]:
            return x
        else:
            return self.find(self.parent[x])
    def union(self,x,y):#将x的老大换成y的老大
        self.parent[self.find(x)] = self.find(y)

    def makeConnected(self, n, connections):
        if len(connections) < n - 1:
            return -1
        self.parent = [i for i in range(n)]
        clusters = n
        for connection in connections:
           x, y = connection
           if self.find(x)!=self.find(y):
               clusters-=1
               self.union(x, y)
               print('==x,y', x, y)
               print('==self.parent:', self.parent)
        print(clusters)
        return clusters-1

n = 4
connections = [[0,1],
               [0,2],
               [1,2]]
sol = Solution()
sol.makeConnected(n, connections)

234.最长连续递增序列

思路:栈


class Solution:
    def findLengthOfLCIS(self, nums):
        stack = []
        res = 0
        for i in range(len(nums)):
            if stack and nums[i]<=stack[-1]:
                stack=[]
            stack.append(nums[i])
            res = max(len(stack), res)
            # print('==stack:', stack)
        # print(res)
        return res
nums = [1, 3, 5, 4, 7]
sol = Solution()
sol.findLengthOfLCIS(nums)

235.由斜杠划分区域

思路;把斜线换成3*3网格,就变成水域问题了

import numpy as np


class Solution:
    def dfs(self, i, j, h, w, matrix):
        if i < 0 or j < 0 or i >= h or j >= w or matrix[i][j] != 0:
            return
        matrix[i][j] = -1
        self.dfs(i - 1, j, h, w, matrix)
        self.dfs(i, j - 1, h, w, matrix)
        self.dfs(i + 1, j, h, w, matrix)
        self.dfs(i, j + 1, h, w, matrix)

    def regionsBySlashes(self, grid):
        n = len(grid)
        matrix = [[0 for _ in range(3 * n)] for _ in range(3 * n)]
        print(np.array(matrix))
        for i in range(n):
            for j in range(len(grid[i])):
                if grid[i][j] == '/':
                    matrix[i * 3][j * 3 + 2] = matrix[i * 3 + 1][j * 3 + 1] = matrix[i * 3 + 2][j * 3] = 1
                elif grid[i][j] == '\\':
                    matrix[i * 3 + 2][j * 3 + 2] = matrix[i * 3 + 1][j * 3 + 1] = matrix[i * 3][j * 3] = 1
        print(np.array(matrix))

        res = 0
        for i in range(3 * n):
            for j in range(3 * n):
                if matrix[i][j] == 0:
                    res+=1
                    self.dfs(i, j, 3 * n, 3 * n, matrix)
        print('==res:', res)
        return res

# grid = [" /", "/ "]
grid = ["/\\", "/\\"]
sol = Solution()
sol.regionsBySlashes(grid)

要注意的是如果格子用2*2,会出现这种0不会挨着的,会出错

236.等价多米诺骨牌对的数量

思路1;

两层循环超时

class Solution:
    def numEquivDominoPairs(self, dominoes):
        #两层循环 超时
        n = len(dominoes)
        left, right = 0, 0
        res=0
        while left<n:
            right=left+1
            while right<n:
                if dominoes[right]==dominoes[left][::-1] or dominoes[right]==dominoes[left]:
                    res+=1
                right+=1
            left+=1
        print('==res:', res)
        return res

思路2:做成字典,记录相同的个数,两两之间相互组合为n*(n-1)/2


class Solution:
    def numEquivDominoPairs(self, dominoes):
        # 字典法
        ans = 0
        dict_ = {}
        for d1, d2 in dominoes:
            # 排序后加入字典
            index = tuple(sorted((d1, d2)))
            if index in dict_:
                dict_[index] += 1
            else:
                dict_[index] = 1
        print('==dict_:', dict_)
        # 计算答案
        for i in dict_:#n*n(-1)/2
            ans += dict_[i] * (dict_[i] - 1) // 2
        return ans

思路3:桶计数,两两之间相互组合为n*(n-1)/2


class Solution:
    def numEquivDominoPairs(self, dominoes):      
        #桶装法
        nums = [0]*100
        res = 0
        for dominoe in dominoes:
            x,y = dominoe
            if x>y:
                nums[x*10+y] +=1
            else:
                nums[y * 10 + x] += 1
        for num in nums:
            if num>=2:
                res += num*(num-1)//2
        print(res)
        return res

239.寻找数组的中心索引

class Solution:
    def pivotIndex(self, nums):
        n = len(nums)
        for i in range(n):
            left_sum = sum(nums[:i])
            right_sum = sum(nums[i+1:])
            if left_sum == right_sum:
                return i
        return -1

nums = [1, 7, 3, 6, 5, 6]
sol = Solution()
res = sol.pivotIndex(nums)
print(res)

240.最小体力消耗路径

思路1:咋一眼看过去,以为直接用dp就行,但是真正在写的过程中,发现消耗的最小体力没有状态转移方程,所以可不可以看成先初始化给一个体力值,如果能达到右下脚,将体力值减少,而这个减少的过程采用二分法这样减少更快

代码注释的部分使用list会超时,换成集合就好了,不会超时


# 思路:二分法,先给定一个初始体力值,能够走到的话,就减少体力,否则增加体力
class Solution:
    def minimumEffortPath(self, heights):
        h, w = len(heights), len(heights[0])
        left_value, right_value, res = 0, 10 ** 6 - 1, 0
        # 二分法
        while left_value <= right_value:  # 终止条件 找到合适的体力值
            mid = left_value + (right_value - left_value) // 2
            # start_point = [[0, 0]]
            # seen = [[0, 0]]
            start_point = [(0, 0)]
            seen = {(0, 0)}
            while start_point:
                x, y = start_point.pop(0)
                for x_, y_ in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                    # 不超过范围 也没见过 差值也小与给定的体力值
                    # if 0 <= x_ < h and 0 <= y_ < w and [x_, y_] not in seen and abs(
                    #         heights[x][y] - heights[x_][y_]) <= mid:
                    #     start_point.append([x_, y_])
                    #     seen.append([x_, y_])
                    if 0 <= x_ < h and 0 <= y_ < w and (x_, y_) not in seen and abs(
                            heights[x][y] - heights[x_][y_]) <= mid:
                        start_point.append((x_, y_))
                        seen.add((x_, y_))
            print('==seen:', seen)
            if (h - 1, w - 1) in seen:  # 足够到底右下角,说明体力足够,那么继续减少体力
                res = mid
                right_value = mid - 1
            else:  # 到不了右下角,说明体力不够,需要增加体力
                left_value = mid + 1
        return res


heights = [[1, 2, 2],
           [3, 8, 2],
           [5, 3, 5]]
sol = Solution()
res = sol.minimumEffortPath(heights)
print('==res:', res)

思路2:并查集
将节点与节点之间的边与权重构建出来
按权重从小到大不断合并只要出现从起始点到终止点能够到达说明找到了此时的值就是最大消耗体力值


#思路:并查集
#将节点与节点之间的边与权重构建出来
#按权重从小到大 不断合并 只要出现从起始点到终止点能够到达 说明找到了 此时的值就是最大消耗体力值
class Solution:
    def find(self, x):
        if x==self.parent[x]:
            return x
        else:
            return self.find(self.parent[x])
    def union(self, x, y):
        #将y的老大换成x的老大
        x = self.find(x)
        y = self.find(y)
        if x == y:
            return False
        if self.size[x]<self.size[y]:
            x, y = y, x
        self.parent[y] = x
        self.size[x] += self.size[y]#x的老大进行计数 看哪边人多 那边人多 就归属
    def connect(self,x, y):
        x,y = self.find(x),self.find(y)
        return x==y

    def minimumEffortPath(self, heights):
        h, w = len(heights), len(heights[0])
        self.parent = [i for i in range(h*w)]
        self.size = [1 for _ in range(h*w)]

        edges = []
        #构建 节点和节点之间的边和权重
        for i in range(h):
            for j in range(w):
                index = i*w+j
                if i>0:
                    edges.append((index-w, index, abs(heights[i][j]-heights[i-1][j])))#减去一行的宽度 回到上一行 也就是竖线的边
                if j>0:
                    edges.append((index-1,index,abs(heights[i][j]-heights[i][j-1])))#减去左边一格  回到左边 也就是横线的边
        print('==edges:', edges)
        print(len(edges))
        edges = sorted(edges, key=lambda x: x[2])#按权重重小到大排序
        print('==edges:', edges)
        res = 0
        for x, y, value in edges:
            self.union(x, y)#把y的老大换成x的老大
            print('==self.parent:', self.parent)
            print('==self.size:', self.size)
            if self.connect(0, h*w-1):
                res = value
                break
        print('==res:', res)
        return res

heights = [[1, 2, 2],
           [3, 8, 2],
           [5, 3, 5]]
# heights  = [[4,3,4,10,5,5,9,2],
#             [10,8,2,10,9,7,5,6],
#             [5,8,10,10,10,7,4,2],
#             [5,1,3,1,1,3,1,9],
#             [6,4,10,6,10,9,4,6]]
sol = Solution()
res = sol.minimumEffortPath(heights)
print('==res:', res)

241.不用加减乘除做加法

思路:分为进位和当前位的异或

class Solution:
    def add(self, a: int, b: int) -> int:
        add_flag = (a&b)<<1;#进位在左移
        sum_ = a^b;#异或 取值 相同为0 不同为1
        return sum_+add_flag

242.水位上升的泳池中游泳

堆队列也称为优先队列就是根节点的值最小

思路:采用bfs + 堆队列保证能到达左下角的时候需要最小的时间


# 堆队列 也称为优先队列 就是根节点的值最小
# 思路:采用dfs + 堆队列
import heapq


class Solution:
    def swimInWater(self, grid):
        h, w = len(grid), len(grid[0])
        res = 0
        heap = [(grid[0][0], 0, 0)]
        visited = {(0, 0)}

        while heap:
            print('===heap:', heap)
            height, x, y = heapq.heappop(heap)
            res = max(res, height)
            if x == w - 1 and y == h - 1:
                return res
            for dx, dy in ((0, 1), (0, -1), (1, 0), (-1, 0)):
                new_x, new_y = x + dx, y + dy
                if 0 <= new_x < w and 0 <= new_y < h and (new_x, new_y) not in visited:
                    visited.add((new_x, new_y))
                    heapq.heappush(heap, (grid[new_x][new_y], new_x, new_y))

        return -1

grid = [[0, 2],
        [1, 3]]
# grid = [[0, 1, 2, 3, 4],
#         [24, 23, 22, 21, 5],
#         [12, 13, 14, 15, 16],
#         [11, 17, 18, 19, 20],
#         [10, 9, 8, 7, 6]]
sol = Solution()
sol.swimInWater(grid)

243.从相邻元素对还原数组

思路:构建字典，进行bfs遍历依次对出现过一次的字符添加进列表即可

#bfs
class Solution():
    def restoreArray(self, adjacentPairs):
        """
        :type adjacentPairs: List[List[int]]
        :rtype: List[int]
        """
        import collections
        memory = collections.defaultdict(list)
        for x,y in adjacentPairs:
            memory[x].append(y)
            memory[y].append(x)
        print('==memory:', memory)
        res = []
        visited = set()
        queue = []
        for key, value in memory.items():
            if len(value) == 1:
                queue.append((key, value[0]))
        while queue:
            print('==queue:', queue)
            start, end = queue.pop()
            res.append(start)
            print('==res:', res)
            visited.add(start)
            for num in memory[end]:
                if num in visited:
                    continue
                queue.append((end, num))
        return res

adjacentPairs = [[2,1],
                 [3,4],
                 [3,2]]
# # adjacentPairs = [[4,-2],
# #                  [1,4],
# #                  [-3,1]]
# # adjacentPairs = [[100000,-100000]]
# adjacentPairs =[[4,-10],
#                 [-1,3],
#                 [4,-3],
#                 [-3,3]]
sol = Solution()
ress= sol.restoreArray(adjacentPairs)
print(ress)

246.公平的糖果棒交换

#思路1:两层for循环超时

#思路1:两层for循环 超时
class Solution:
    def fairCandySwap(self, A, B):
        sum_A = sum(A)
        sum_B = sum(B)
        target = (sum_A+sum_B)//2
        for i in range(len(A)):
            for j in range(len(B)):
                if sum(A[:i])+sum(A[i+1:])+B[j] == target:
                    return [A[i], B[j]]
        return []

# A = [1, 2]
# B = [2, 3]
A = [1 ,2, 5]
B = [2, 4]
sol = Solution()
res = sol.fairCandySwap(A, B)
print(res)

思路2:双指针利用 sumA-x+y = sumB+x-y -->(sumA-sumB)/2 = x-y 转换为寻找两个元素

#思路1:#sumA-x+y = sumB+x-y -->(sumA-sumB)/2 = x-y
# 故用双指针 转换为二分查找 去查找两数之差
class Solution:
    def fairCandySwap(self, A, B):
        i = 0
        j = 0
        A = sorted(A)
        B = sorted(B)
        sum_A  = sum(A)
        sum_B = sum(B)
        target = (sum_A-sum_B)/2
        print('==target:', target)
        while i<len(A) and j<len(B):
            if (A[i] - B[j]) == target:
                return [A[i], B[j]]
            elif (A[i] - B[j])>target:
                j+=1
            else:
                i+=1
        return []

# A = [1, 2]
# B = [2, 3]
A = [1,2,5]
B = [2,4]
sol = Solution()
res = sol.fairCandySwap(A, B)
print(res)

思路3:一层for循环利用 sumA-x+y = sumB+x-y -->(sumA-sumB)/2 = x-y 转换为寻找两个元素

#思路2:#sumA-x+y = sumB+x-y -->(sumA-sumB)/2 = x-y
# 一层for循环走遍
class Solution:
    def fairCandySwap(self, A, B):
        sum_A = sum(A)
        sum_B = sum(B)
        target = (sum_A-sum_B)//2
        for num in B:
            if num+target in A:
                return [num+target, num]
        return []

A = [1, 2]
B = [2, 3]
# A = [1 ,2, 5]
# B = [2, 4]
sol = Solution()
res = sol.fairCandySwap(A, B)
print(res)

247.替换后的最长重复字符

思路:如果k==0其实就是求最长字符串 ,k大于0,那么采用滑动窗口的方式对左右指针求最少字符(也可能是不同字符)个数

如果最少字符个数大于k说明左指针该右移动了,否则右指针一直在右移

# 思路:如果k==0其实就是求最长字符串 ,k大于0,那么采用滑动窗口的方式 对左右指针求最少字符个数
# 如果最少字符个数大于k说明 左指针改右移动了,否则右指针一直在右移
class Solution:
    def characterReplacement(self, s, k):
        left, right = 0, 0
        nums = [0] * 26
        # max_num = 0
        res = 0
        while right < len(s):
            nums[ord(s[right]) - ord('A')] += 1
            max_num = max(nums)
            #减去max_num 就是 求左右指针内最少字符(也可能是不同字符)个数
            while right - left + 1 - max_num > k:
                nums[ord(s[left]) - ord('A')] -= 1
                left += 1
            right += 1
            res = max(right - left, res)
        print('==res:', res)
        return res


# s = "ABAB"
# k = 2
s = "AABABBA"
k = 1
sol = Solution()
res = sol.characterReplacement(s, k)
print('==res:', res)

250.子数组最大平均数 I

思路1:采用list和 ,超时

class Solution:
    def findMaxAverage(self, nums, k):
        res = float('-inf')
        for i in range(len(nums)-k+1):
            res = max(sum(nums[i:i+k]), res)
        print(res)
        return res/k

nums = [1, 12, -5, -6, 50, 3]
k = 4
sol = Solution()
sol.findMaxAverage(nums, k)

思路2:采用前缀和,空间换时间

class Solution:
    def findMaxAverage(self, nums, k):
        length =len(nums)
        pre_sum = [0]*length
        pre_sum[0] = nums[0]
        for i in range(1, length):
            pre_sum[i] = pre_sum[i-1]+nums[i]
        print('===pre_sum:', pre_sum)

        res = float('-inf')
        for i in range(k-1, length):
            if i > k-1:
                res = max(res, pre_sum[i] - pre_sum[i-k])
            else:
                res = pre_sum[i]
        print('==res:', res)
        return res/k


nums = [1, 12, -5, -6, 50, 3]
k = 4
sol = Solution()
res = sol.findMaxAverage(nums, k)
print('==res:', res)

思路3:双指针

class Solution:
    def findMaxAverage(self, nums, k):
        length = len(nums)
        Sum = 0
        res = float('-inf')
        left,right=0,0
        while right<length:
            Sum += nums[right]
            if right>=k-1:
                res =max(res, Sum)
                print('==res:', res)
                Sum-=nums[left]
                left += 1
            right+=1
        return res/k

nums = [1, 12, -5, -6, 50, 3]
k = 4
sol = Solution()
res = sol.findMaxAverage(nums, k)
print('==res:', res)

251.尽可能使字符串相等

思路;转换成距离列表后进行双指针滑动窗口即可

#双指针
class Solution:
    def equalSubstring(self, s, t, maxCost):
        length = len(s)
        dist_cost = [0] * length
        for i in range(length):
            dist_cost[i] = abs(ord(s[i]) - ord(t[i]))
        print('==dist_cost:', dist_cost)
        res = 0
        left,right =0,0
        Sum = 0
        while right<length:
            Sum+=dist_cost[right]
            if Sum>maxCost:
                Sum -= dist_cost[left]
                left+=1
            right+=1
            res = max(res, right - left)
        print(res)
        return res
# s = "abcd"
# t = "bcdf"
# cost = 3
# s = "abcd"
# t = "acde"
# cost = 0
s = "krrgw"
t = "zjxss"
cost = 19
# s = "abcd"
# t = "cdef"
# cost = 3
sol = Solution()
sol.equalSubstring(s, t, cost)

261.可获得的最大点数

思路:转换为求连续的和最小, 那么自然用滑动窗口解决即可以

class Solution:
    def maxScore(self, cardPoints, k):
        length = len(cardPoints)
        leaving_k = length - k
        print('==leaving_k:', leaving_k)
        if leaving_k == 0:
            return sum(cardPoints)

        left, right = 0, 0
        min_res = float('inf')
        temp_res = 0
        while right < length:
            temp_res += cardPoints[right]
            if right >= leaving_k - 1:
                min_res = min(min_res, temp_res)
                print('==temp_res:', temp_res)
                left += 1
                temp_res -= cardPoints[left - 1]
            right += 1
        print('==min_res:', min_res)
        return sum(cardPoints) - min_res

cardPoints = [1, 2, 3, 4, 5, 6, 1]
k = 3
# cardPoints = [9, 7, 7, 9, 7, 7, 9]
# k = 7
sol = Solution()
sol.maxScore(cardPoints, k)

262.非递减数列

思路:分别从左右两边判断是否递增

class Solution:
    def checkPossibility(self, nums: List[int]) -> bool:
        length = len(nums)
        # res = 0
        left,right = 0,length-1
        while left<length-1 and nums[left]<=nums[left+1]:
            left+=1
        if left==length-1:
            return True
        while right>=0 and nums[right-1]<=nums[right]:
            right-=1
        if right - left>1:
            return False
        if left==0 or right==length-1:
            return True
        
        if nums[right+1]>=nums[left] or nums[left-1]<=nums[right]:
            return True

        return False

264.最长湍流子数组

思路:双指针

满足山峰:arr[right]>arr[right-1] and arr[right]>arr[right+1] right+=1

满足山谷:arr[right]

其他时候 left移动到right位置


class Solution:
    def maxTurbulenceSize(self, arr):
        left, right = 0, 0
        length = len(arr)
        res = 1
        while right<length-1:
            if left==right:
                if left+1<length and arr[left]==arr[left+1]:
                    left+=1
                right+=1
            else:#山峰
                if right+1<length and arr[right]>arr[right-1] and arr[right]>arr[right+1]:
                    right+=1
                # 山谷
                elif right+1<length and arr[right]<arr[right-1] and arr[right]<arr[right+1]:
                    right+=1
                else:
                    left=right
            print('==right:', right)
            res = max(res, right-left+1)
        print('==res:', res)
        return res


# arr  = [9,4,2,10,7,8,8,1,9]
# arr = [100]
arr = [2,1]
sol = Solution()
sol.maxTurbulenceSize(arr)

267.数据流中的第 K 大元素

思路1:每个add进去就sort取第k大，时间复杂度偏大k*log(k),对于这种取topk问题，用最小堆更合适

#k*O(logk)  超时
class KthLargest:

    def __init__(self, k, nums):
        self.k = k
        self.nums = nums

    def add(self, val):
        self.nums.append(val)
        self.nums = sorted(self.nums)[::-1]
        return self.nums[self.k - 1]
k = 3
nums = [4, 5, 8, 2]
sol = KthLargest(k, nums)
res = sol.add(3)
print('=res:', res)
res = sol.add(5)
print('=res:', res)
res = sol.add(10)
print('=res:', res)
res = sol.add(9)
print('=res:', res)
res = sol.add(4)
print('=res:', res)

思路2:最小堆，保证最小堆中只有k个元素，那么堆顶自然就是第k大元素

时间复杂度为log(k),因为push和pop都是log(k).

python代码

# 最小堆 topk都用最小堆
import heapq
class KthLargest(object):

    def __init__(self, k, nums):
        """
        :type k: int
        :type nums: List[int]
        """
        self.k = k
        self.que = nums
        heapq.heapify(self.que)

    def add(self, val):
        """
        :type val: int
        :rtype: int
        """
        heapq.heappush(self.que, val)
        print('=====self.que====:', self.que)
        while len(self.que)>self.k:#保持最小堆中只有k个元素 则堆顶就是第k大元素
            heapq.heappop(self.que)
        print('clean self.que:', self.que)
        return self.que[0]

k = 3
nums = [4, 5, 8, 2]
sol = KthLargest(k, nums)
res = sol.add(3)
print('=res:', res)
res = sol.add(5)
print('=res:', res)

c++代码:

#include <map>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;

class KthLargest {
public:
    priority_queue<int, vector<int>, greater<int> > que;//最小堆
    int k;
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        for(int k=0;k<nums.size();k++)
        {
            que.push(nums[k]);
            if (que.size()>this->k)
            {
                que.pop();
            }
        }
    }
    
    int add(int val) {
        que.push(val);
        if(que.size()>this->k)
        {
            que.pop();
        }
        return que.top();
    }
};

int main()
{   
    int k=3;
    vector<int> nums;
    nums={4,5,8,2};
    KthLargest *p = new KthLargest(k, nums);
    int res = p->add(3);
    cout<<"res:"<<res<<endl;
    res = p->add(5);
    cout<<"res:"<<res<<endl;
    res = p->add(10);
    cout<<"res:"<<res<<endl;
    res = p->add(9);
    cout<<"res:"<<res<<endl;
    res = p->add(4);
    cout<<"res:"<<res<<endl;

    delete p;
    p=NULL;
    return 0;

}

269.杨辉三角 II

思路:一层一层遍历出值即可

python代码:

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        temp = [0]*(rowIndex+1)
        temp[0] = 1
        for i in range(1, rowIndex+1):
            for j in range(i, 0, -1):
                temp[j] += temp[j-1]
            # print('==temp:', temp)
        return temp

c++代码:

#include <map>
#include <vector>
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> temp(rowIndex+1, 0);
        temp[0] = 1;
        for (int i=1;i<rowIndex+1;i++)
        {
            for(int j=i;j>0;j--)
            {
                temp[j]+=temp[j-1];
            } 
        }
        return temp;
    }
};

int main()
{   
    Solution *p = new Solution();
    int row_index = 3;
    vector <int> res;
    res = p->getRow(row_index);
    for(int k=0;k<res.size();k++)
    {
        cout<<"res[k]"<<res[k]<<endl;
    }
    p=NULL;
    delete p;
    return 0;
}

271.找到所有数组中消失的数字

思路1:hash 空间复杂度 o(n) 时间复杂度o(n)

# 空间复杂度 o(n) 时间复杂度o(n)
class Solution:
    def findDisappearedNumbers(self, nums):
        dict_={}
        for i in range(len(nums)):
            dict_[nums[i]] = dict_.get(nums[i],0)+1

        res = []
        for i in range(len(nums)):
            if i+1 not in dict_:
                res.append(i+1)
        print(res)
        return res

思路2:求出索引在对应位置处添加长度如果没有的数字,则数字就小于等于长度

空间复杂度O(1) 时间复杂度O(n)

#空间复杂度O(1) 时间复杂度O(n)
class Solution:
    def findDisappearedNumbers(self, nums):
        length = len(nums)
        for i in range(len(nums)):
            index= (nums[i]-1)%length
            nums[index] +=length
        print('==nums:', nums)
        res = [i+1 for i in range(length) if nums[i] <= length]
        print(res)
        return res

# nums = [4,3,2,7,8,2,3,1]
nums = [1,2,2,3,3,4,7,8]
# nums = [1,2,3,3,5,6,7]
sol = Solution()
sol.findDisappearedNumbers(nums)

c++代码:

#include <map>
#include <vector>
#include <iostream>
#include <queue>
#include <string>
#include <algorithm>
using namespace std;
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> res;
        for (int i=0;i<nums.size();i++)
        {
            int index = (nums[i]-1)%nums.size();
            nums[index] += nums.size();
        }
        for (int i=0;i<nums.size();i++)
        {
            if(nums[i]<=nums.size())
            {
                res.push_back(i+1);
            }
        }
        return res;
    }
};

int main()
{
    Solution *p = new Solution();
    vector <int >nums;
    nums = {4,3,2,7,8,2,3,1};
    vector <int> res = p->findDisappearedNumbers(nums);
    for(int i=0;i<res.size();i++)
    {
        cout<<"res:"<<res[i]<<endl;    
    }
    
    delete p;
    p = NULL;
    return 0;
}

272.情侣牵手

思路:其实就是将环拆开，0,1都看成第0对，2,3看成第1对

可看出要交换的座位就是环的边数减去1,对于这种去环问题，自然想到并查集

python代码:

class Solution:
    def find(self,x):
        if self.parent[x]==x:
            return x
        return self.find(self.parent[x])
    def union(self,i,j):#将i的老大变成j的老大
        self.parent[self.find(i)] = self.find(j)
    def get_count(self,n):
        for i in range(n):
            self.count[self.find(i)]+=1
    def minSwapsCouples(self, row):
        n = len(row)//2
        self.parent = [i for i in range(n)]
        self.count = [0 for i in range(n)]
        print('===init self.parent', self.parent)
        for i in range(0, len(row), 2):
            self.union(row[i]//2, row[i+1]//2)
            print('==self.parent:', self.parent)
        self.get_count(n)
        print('===self.count:', self.count)
        res = 0
        for i in range(n):
            res += max(self.count[i]-1, 0)
        print(res)
        return res

# row = [0,2,2]
# row = [0, 2, 1, 3]
# row = [2,0,5,4,3,1]
row = [1,4,0,5,8,7,6,3,2,9]
# row = [0, 1, 2, 3]
sol = Solution()
sol.minSwapsCouples(row)

c++代码:

#include <map>
#include <vector>
#include <iostream>
#include <queue>
#include <string>
#include <algorithm>
using namespace std;

class Solution {
public:
    vector<int> parent;
    vector<int> count;
    int find(int x)
    {
        if(x==parent[x])
        {
            return x;
        }
        return find(parent[x]);
    }
    //把i的老大换成j的老大
    void merge(int i, int j)
    {
        parent[find(i)]=find(j);
    }
    void get_count(int n)
    {
        for (int i=0;i<n;i++)
        {   
            count[find(i)]+=1;
        }
    }
    int minSwapsCouples(vector<int>& row) {
        int n = row.size()/2;
        cout<<n<<endl;
        int res=0;
        for(int i=0;i<n;i++)
        {
            parent.push_back(i);
            count.push_back(0);
        }
        for(int i=0;i<row.size();i+=2)
        {
            merge(row[i]/2,row[i+1]/2);
        }
        get_count(n);
        // // //debug 
        // for (int i=0;i<parent.size();i++)
        // {
        //     cout<<"===parent[i]"<<parent[i]<<endl;
        // }
        //debug 
        // for (int i=0;i<count.size();i++)
        // {
        //     cout<<"===count[i]"<<count[i]<<endl;
        // }
        for (int i=0;i<count.size();i++)
        {
            res+=max(count[i]-1,0);
        }

        return res;
    }
};
int main()
{
    Solution *p = new Solution();
    vector<int> row;
    row = {0, 2, 1, 3};
    int res = p->minSwapsCouples(row);
    cout<<"==res:"<<res<<endl;
    delete p;
    p=NULL;
    return 0;
}

273.最大连续1的个数

思路1:直接数1个数

class Solution:
    def findMaxConsecutiveOnes(self, nums):
        count_one = 0
        res = 0
        for i in range(len(nums)):
            if nums[i]==1:
                count_one+=1
            else:
                count_one=0
            res = max(res, count_one)
        # print(res)
        return res

思路2：dp

class Solution:
    def findMaxConsecutiveOnes(self, nums):
        res = [-1]
        for i in range(len(nums)):
            if nums[i]==0:
                res.append(i)
        res.append(len(nums))
        print(res)
        if len(res)==1:
            return res[-1]
        max_length = 0
        for i in range(1, len(res)):
            max_length = max(res[i]-res[i-1]-1, max_length)
        print(max_length)
        return max_length

思路3：双指针滑动窗口

class Solution:
    def findMaxConsecutiveOnes(self, nums):
        left,right=0,0
        res = 0
        while right<len(nums):
            if nums[right]==1:
                right+=1
            else:
                right+=1
                left=right
            print('==left,right:', left, right)
            res = max(res, right - left)
            print('==res:', res)
        return res

c++双指针:

#include <vector>
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        int left=0;
        int right = 0;
        int res = 0;
        while (right<nums.size())
        {
            if(nums[right]==1)
            {
                right++;
            }
            else
            {                   
                right++;
                left=right;                
            }
            res = max(right-left, res);
        }
        return res;        
    }
};

int main()
{
    Solution *p = new Solution();
    vector<int> nums;
    nums = {1,1,0,1,1,1};
    int res = p->findMaxConsecutiveOnes(nums);
    cout<<"==res:"<<res<<endl;
    delete p;
    p=NULL;
    return 0;
}

274.重塑矩阵

思路:对于h*w的元素个数，索引为h_index = i//rows,w_index = i%rows

python代码

class Solution:
    def matrixReshape(self, nums: List[List[int]], r: int, c: int) -> List[List[int]]:
        h = len(nums)
        w = len(nums[0])
        if h*w != r*c:
            return nums

        res = [[0 for _ in range(c)] for _ in range(r)]
        # print(res)
        for i in range(h*w):
            res[i//c][i%c] = nums[i//w][i%w]
        # print(res)
        return res

c++代码:

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
        int h = nums.size();
        int w = nums[0].size();
        // cout<<"==h:"<<h<<endl;
        vector<vector<int>> res(r ,vector<int>(c,0));  //初始化c*r元素为0的矩阵 
        
        // cout<<"==res.size():"<<res.size()<<endl;
        // cout<<"==res[0].size():"<<res[0].size()<<endl;
        if(h*w!=r*c)
        {
            return nums;
        }
        for (int i=0;i<h*w;i++)
        {   
            // cout<<"i/w:"<<i/w<<endl;
            // cout<<"i%w:"<<i%w<<endl;
            res[i/c][i%c] = nums[i/w][i%w];
        }
        return res;
    }
};

275.最大连续1的个数 III

思路:其实就是滑动窗口判断有大于K个0的则左指针右移动，之所以用大于K来判断是因为0后续可能会跟着很多1,所以大于K的话，会把这些包含进去,和https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/ 思想一样

python:

class Solution:
    def longestOnes(self, A: List[int], K: int) -> int:
        left,right =0,0
        n = len(A)
        zero_count =0
        res = 0
        while right<n:
            if A[right]==0:
                zero_count+=1
            #left向右收缩
            while zero_count>K:#大于K个0的时候就说明找到符合条件的了
                if A[left]==0:
                    zero_count-=1
                left+=1
            res = max(res, right - left + 1)
            # print('=left:', left)
            # print('==right:', right)
            # print('==res:', res)
            right+=1
        # print(res)
        return res

c++

class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        int left=0;
        int right =0;
        int res=0;
        int zero_count =0;
        int length = A.size();
        while(right<length)
        {   
            if (A[right]==0)
            {
                zero_count++;
            }
            while (zero_count>K)
            {   
                if (A[left]==0)
                {
                    zero_count--;
                }
                left++;
            }
            res = max(res, right-left+1);
            
            right++;
        }
        return res;

    }
};

276.数组的度

思路:三个hash,一个计度，一个记录左索引，一个记录右索引

python:

class Solution:
    def findShortestSubArray(self, nums: List[int]) -> int:
        dict_ = {}
        left_index_dict = {}
        right_index_dict = {}
        for i in range(len(nums)):
            dict_[nums[i]] = dict_.get(nums[i], 0)+1
            if nums[i] not in left_index_dict:
                left_index_dict[nums[i]] = i
            right_index_dict[nums[i]] = i
        # print('==dict_:', dict_)
        # print('=left_index_dict:', left_index_dict)
        # print('==right_index_dict:', right_index_dict)
        dict_ = dict(sorted(dict_.items(), key=lambda x:x[1],reverse=True))
        # print(dict_)
        max_degree = 0
        res = float('inf')
        for key,value in dict_.items():
            max_degree = value
            break
        # print(max_degree)
        for key, value in dict_.items():
            if value==max_degree:
                res = min(res, right_index_dict[key] - left_index_dict[key]+1)
        # print('===res:',res)
        return res

c++:

class Solution {
public:
    int findShortestSubArray(vector<int>& nums) {
        map<int, int>dict_;
        map<int, int>left_index_dict;
        map<int, int>right_index_dict;
        for(int i=0;i<nums.size();i++){
            dict_[nums[i]]++;
            if(left_index_dict.count(nums[i])==0){
                left_index_dict[nums[i]] = i;
            }
            right_index_dict[nums[i]] = i;
        }
        int max_degree=0;
        map<int,int>::iterator iter=dict_.begin();
        for (;iter!=dict_.end();iter++)
        {
            max_degree = max(max_degree, iter->second);
        }
        int res=INT_MAX;
        map<int,int>::iterator iter_2=dict_.begin();
        for (;iter_2!=dict_.end();iter_2++)
        {
            if (max_degree == iter_2->second){
                res = min(res, right_index_dict[iter_2->first] - left_index_dict[iter_2->first]+1);
            }
        }
        return res;

    }
};