http://mathworld.wolfram.com/GeneralizedFourierSeries.html
Generalized Fourier Series
A generalized Fourier series is a series expansion of a function based on the special properties of acomplete orthogonal system of functions. The prototypical example of such a series is theFourier series, which is based of the biorthogonality of the functions![]() and
and![]() (which form acomplete biorthogonal system under integration over the range
(which form acomplete biorthogonal system under integration over the range ![]() . Another common example is theLaplace series, which is a double series expansion based on the orthogonality of thespherical harmonics
. Another common example is theLaplace series, which is a double series expansion based on the orthogonality of thespherical harmonics![]() over
over![]() and
and![]() .
.
Given a complete orthogonal system of univariate functions ![]() over the interval
over the interval![]() , the functions
, the functions![]() satisfy an orthogonality relationship of the form
satisfy an orthogonality relationship of the form
|
(1)
|
over a range ![]() , where
, where![]() is aweighting function,
is aweighting function,![]() are given constants and
are given constants and![]() is theKronecker delta. Now consider an arbitrary function
is theKronecker delta. Now consider an arbitrary function![]() . Write it as a series
. Write it as a series
|
(2)
|
and plug this into the orthogonality relationships to obtain
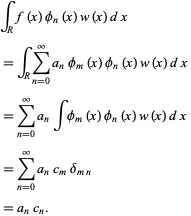 |
(3)
|
Note that the order of integration and summation has been reversed in deriving the above equations. As a result of these relations, if a series for![]() of the assumed form exists, its coefficients will satisfy
of the assumed form exists, its coefficients will satisfy
|
(4)
|
Given a complete biorthogonal system of univariate functions, the generalized Fourier series takes on a slightly more special form. In particular, for such a system, the functions![]() and
and![]() satisfy orthogonality relationships of the form
satisfy orthogonality relationships of the form
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
|
for ![]() over a range
over a range![]() , where
, where![]() and
and![]() are given constants and
are given constants and![]() is theKronecker delta. Now consider an arbitrary function
is theKronecker delta. Now consider an arbitrary function![]() and write it as a series
and write it as a series
![f(x)=sum_(n=0)^inftya_nf_1(n,x)+sum_(n=0)^inftyb_nf_2(n,x) =f_1(0)a_0+sum_(n=1)^inftya_nf_1(n,x)+f_2(0)b_0+sum_(n=1)^inftyb_nf_2(n,x) =[f_1(0)a_0+f_2(0)b_0]+sum_(n=1)^inftya_nf_1(n,x)+sum_(n=1)^inftyb_nf_2(n,x) =e+sum_(n=1)^inftya_nf_1(n,x)+sum_(n=1)^inftyb_nf_2(n,x)](https://i-blog.csdnimg.cn/blog_migrate/fe2c8e5149d06a383ec3a7f8f29e7a70.gif) |
(10)
|
and plug this into the orthogonality relationships to obtain
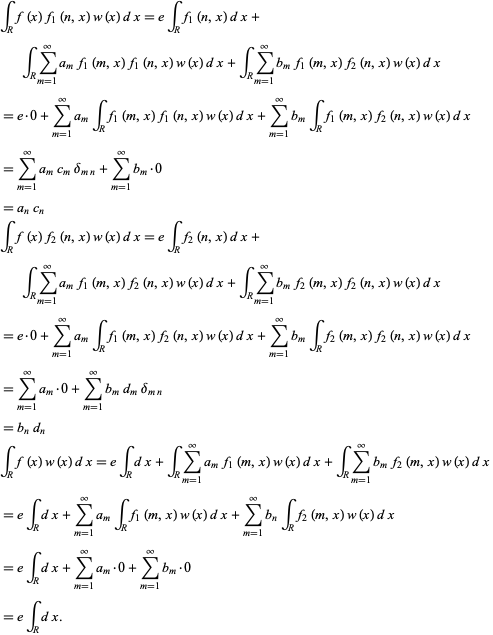 |
(11)
|
As a result of these relations, if a series for ![]() of the assumed form exists, its coefficients will satisfy
of the assumed form exists, its coefficients will satisfy
|
(12)
| |||
|
(13)
| |||
|
(14)
|
The usual Fourier series is recovered by taking ![]() and
and![]() which form a complete orthogonal system over
which form a complete orthogonal system over![]() withweighting function
withweighting function![]() and noting that, for this choice of functions,
and noting that, for this choice of functions,
|
(15)
| |||
|
(16)
|
Therefore, the Fourier series of a function ![]() is given by
is given by
|
(17)
|
where the coefficients are
|
(18)
| |||
|
(19)
| |||
|
(20)
|





 本文介绍了广义傅立叶级数的概念及其数学原理,包括正交函数系、双正交函数系的性质及应用,展示了如何利用这些性质进行函数展开。
本文介绍了广义傅立叶级数的概念及其数学原理,包括正交函数系、双正交函数系的性质及应用,展示了如何利用这些性质进行函数展开。
















 7938
7938

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








