【AT2301】 Solitaire

题目链接：AT2301 Solitaire
（翻译在讨论版中有）

解法

首先要绕一下思维，考虑一个合法排列（即弹出的数的排列）的性质。可以得到它满足：

1、第$k$个数是$1$（题目条件）

2、前$k-1$个数可以拆成一个或两个单调递减的序列。（由于我们是按序插入，所以未弹出前的序列在$[1,k-1]$上递减，在$[k+1,n]$上递增。而弹出时是选择两端中的一端弹出，拆开弹出的序列，一部分为前端弹出的数，另一部分为后端弹出的数，于是这两部分就是单调递减的。）

3、前$k-1$个数中其中一个序列的最小值一定大于后$n-k$个数中的最大值。

关于3的证明：

我们将前$k-1$个数的两个单调递减的序列记为$A,B$，由于我们要令第$k$个数为$1$，也就是说$A$或$B$中有一个数在弹出前在序列中与$1$相邻。我们设图中的蓝色区域为已弹出的前$k-1$个数：

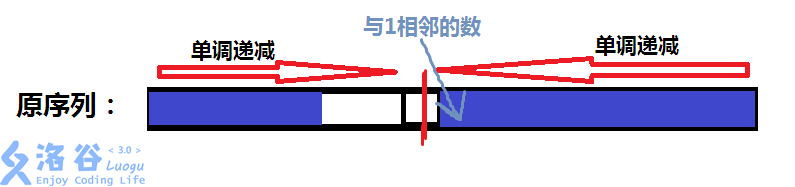
也就是说另一个蓝色区域中的数（设为$u$，由于$B$单调递减，$u=\min\left\{B\right\}$）大于剩余未弹出的$n-k$个数的最大值（白色区域，最大值为$u$的相邻数）。

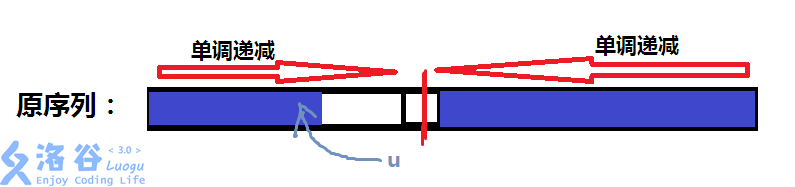
于是我们接着考虑如何构造序列。

先考虑后$n-k-1$个数，这些数一定构成一个单调队列，若确定了前$k-1$，然后将$1$弹出，剩余的数即可任意弹出，方案数为$2^{n-k-1}$

然后确定前$k-1$个数。$f_{i,j}$表示，前$k-1$个数中，已确定了$i$个数，这些数的最小值为$j$。

不妨设第二个序列$B$满足性质3，即$u$大于剩余数的最大值。每次新加一个数，如果加进$A$，那么因为当前的$A$要一直弹出直到$1$出现为止，所以新加的数一定小于$j$，于是$f_{i,j}\rightarrow f_{i+1,k} (j>k)$，如果加进$B$，加入的数就要是当前没加的数中最大的（即小于$\min\{B\}$），因为只有这样才能满足性质3。
于是$f[i][j]\rightarrow f_{i+1,j}$。

代码：

#include<iostream>
#include<cstdio>

using namespace std;

const long long P=1000000007ll;
long long n,k,f[10001];

long long qpow(long long a,int x){
    if(x<0)return 1;
    long long s=1ll;
    while(x){if(x&1)(s*=a)%=P;(a*=a)%=P;x>>=1;}
    return s;
}

int main(){
    scanf("%lld%lld",&n,&k);
    f[0]=1ll;
    for(int i=1;i<n;++i){for(int j=i;j;--j)f[j]=(f[j+1]+f[j-1])%P;f[0]=f[1];}
    printf("%lld",f[n-k]*qpow(2ll,n-k-1)%P);
}