Knight On the Chessboard-优快云博客

本文链接：https://blog.youkuaiyun.com/exm_further/article/details/122988222

这篇博客探讨了LeetCode688题目的解决方案，主要涉及动态规划和递归算法。作者首先尝试使用递归方法，但由于时间复杂度过高导致超时。然后，作者转向动态规划，通过反向计算每一步的概率，从最后一步（k=0）开始，逐步向前推导，最终得到在k步后骑士仍在棋盘上的概率。动态规划方法提高了效率，通过滚动迭代的空间优化进一步减少了空间开销。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Leetcode 688: 骑士在棋盘上的概率

Definition:

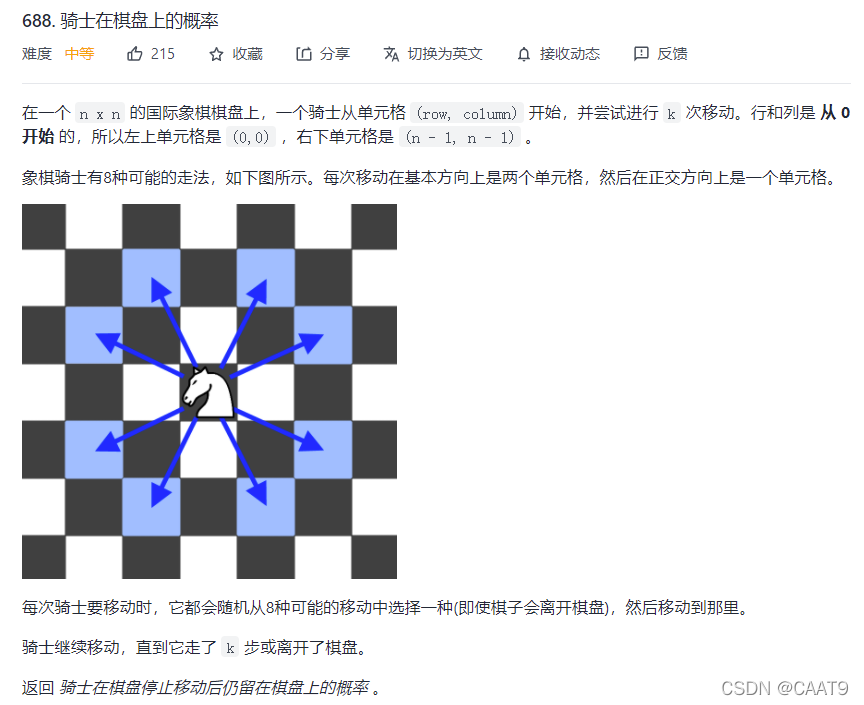
在这里插入图片描述

思路

由于刷题尹始对DP和DFS之类的问题还没有什么概念，看到题目第一想法就是直接正向求解，在使用递归实现基本问题的求解之后发现对于k较大的情形递归的方法就失效了，直接超时。后来在评论里面也看到不少老哥用递归超时的，其实思路很简单，但是就是无法AC。
对于每一个起始位置，我们可以通过计算在下一步有多少种可能的走法，找出下一步所有可能的位置以及对应的概率之后，不断向后迭代，最终只留下了能够不离开棋盘的所有步数对应的概率，求和即可得到最终的结果，代码如下

class Solution:
    def possible_position(self, n: int, row: int, col:int):
        positions = []
        if row - 2 >= 0:
            if col - 1 >= 0:
                positions.append((row - 2, col - 1))
            if col + 1 < n:
                positions.append((row - 2, col + 1))

        if row - 1 >= 0:
            if col - 2 >= 0:
                positions.append((row - 1, col - 2))
            if col + 2 < n:
                positions.append((row - 1, col + 2))

        if row + 1 < n:
            if col - 2 >= 0:
                positions.append((row + 1, col - 2))
            if col + 2 < n:
                positions.append((row + 1, col + 2))

        if row + 2 < n:
            if col - 1 >= 0:
                positions.append((row + 2, col - 1))
            if col + 1 < n:
                positions.append((row + 2, col + 1))

        return positions

    def knightProbability(self, n: int, k: int, row: int, column: int) -> float:
        possible_pos = self.possible_position(n, row, column)
        possibility = len(possible_pos) / 8

        if k == 0 and (0 <= row < n) and (0 <= column < n):
            return 1

        if k == 1:
            return possibility

        candidates = []
        for pos in possible_pos:
            if not ((0 <= row < n) or (0 <= column < n)):
                continue
            candidates.append(possibility * (1 / len(possible_pos)) * self.knightProbability(n, k - 1, pos[0], pos[1]))
        return sum(candidates)

以上是使用递归进行求解的代码实现，该方法在实际运行时存在超时的问题。在阅读官方题解之后，了解了什么是动态规划并对官方给出的代码进行了理解，下面是其给出的解题方法：

class Solution:
    def knightProbability(self, n: int, k: int, row: int, column: int) -> float:
        dp = [[[0] * n for _ in range(n)] for _ in range(k + 1)]
        for step in range(k + 1):
            for i in range(n):
                for j in range(n):
                    if step == 0:
                        dp[step][i][j] = 1
                    else:
                        for di, dj in ((-2, -1), (-2, 1), (-1, -2), (-1, 2), (1, -2), (1, 2), (2, -1), (2, 1)):
                            ni, nj = i + di, j + dj
                            if 0 <= ni < n and 0 <= nj < n:
                                dp[step][i][j] += dp[step - 1][ni][nj] / 8
        return dp[k][row][column]

可以看到，使用动态规划的方法思路非常简洁。使用一个三维数组，第一个维度是channel（也就是step）维度，另外两个维度对应棋盘的行和列。这里其实使用了逆向思维，因为正向推理的过程中可能性非常多，但是反过来考虑的话，如果到了最后一步（k=0）骑士仍旧在棋盘上（此时概率为1，因为没有了后续步骤，骑士已经固定在棋盘上），那么就可以推理在k=1时其在棋盘上的可能位置并计算在对应位置的概率（例如在k=0时骑士在棋盘上的 $(r o w, c o l u m n)$ 位置，那么在上一步中其可能存在的位置是可以计算的，即 $d p [s t e p - 1] [r o w + d i] [c o l u m n + d j]$ ），通过反向求解概率直到求得step=k时，便可获得最终结果。

题后反思

本题在题目设置上的技巧在于棋盘格的大小n是固定的，这也就决定了在使用动态规划时状态变量的个数是固定的，因此通过这种反向求解的思路效率较高。值得一提的是，由于当前的状态仅仅与上一步状态有关，因此状态数组的实际大小可以设置为size = (2, n, n) 通过滚动迭代的方式进一步节省空间开销。