优化问题|文化基因算法求解分布式柔性作业车间调度问题

最新推荐文章于 2024-11-21 09:13:10 发布

eternal1995

最新推荐文章于 2024-11-21 09:13:10 发布

阅读量1k

点赞数 21

文章标签：算法分布式

本文链接：https://blog.youkuaiyun.com/eternal1995/article/details/141293762

版权

问题描述

在智能制造日益发展的背景下，企业生产模式逐步从单一工厂制造转变为多工厂协同的分布式制造。该模式能够有效地减少规模效应，实现资源的合理配置，进而降低成本和提高生产效率。在此背景下的分布式柔性作业车间调度问题(Distributed flexible job shop scheduling problem，DFJSP)被众多学者广泛关注和研究，DFJSP 是传统柔性作业车间与分布式车间调度问题的一个结合。

分布式柔性作业车间调度（Distributed FJSP，DFJSP）主要包含工序序列、机器的选择和工厂的选择三个子问题。首先将𝑛个工件分配到不同的工厂当中，然后在每个工厂为工件选择可加工的机器以及确定工件的加工顺序。该问题的主要目标是通过调整工件在哪个工厂加工、工件序列的排序以及工件选择哪台机器加工，从而实现最小化最大完工时间的目标。

分布式柔性作业车间系统示意图

模型构建

DFJSP 可描述如下：给定的 $n$ 个加工工件，在 $N_f$ 个工厂中加工，每个工厂有 $m_f$ 台机床。每个工件 $i$ 可选择在任一工厂加工。并且，每个工件 $i$ 包含
$n_i$ 道工序，工序 $O_{i,j}$ 可选在工厂 $f$ 中的 $m_{i,j,f}$ 个加工机床上加工。

DFJSP 的假设条件如下：

（1）所有工件、机器以及工厂在零时刻都可用；

（2）每个机器在同一时刻只能处理一个工序；

（3）工件在加工处理过程中不能被中断；

（4）工件的所有工序都按照预先设定好的顺序，不允许提前或者推后；

（5）一个工件只能在一个工厂中处理，同时一个工序只能在一台机器处理；

（6）不考虑机器故障和准备时间；

参数变量：

数学模型：

算法思路

文化基因算法(Memetic ALgorithm)，由Mpscato在1989年提出的。文化基因算法是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体，可以简单理解为：Memetic = GA + Local Search。其中，局部搜索算子可以根据不同的策略进行设计，比如常用的爬山机制、模拟退火、贪婪机制、禁忌搜索等。

基因编码

针对 DFJSP，目前主要有4种离散编码方法。

1）基于工件序列的编码(SJS)，编码中只包含工件序列，工序排序、机器选择以及工厂选择 3 个子问题都在解码过程中分别通过相应的规则确定；

2）基于工序序列的编码(SOP)，SOP 中只包含工序序列，用来确定工序的先后顺序，工厂选择以及机器选择在解码过程中同样通过规则方法进行确定；

3）基于工序和工厂序列的编码(SGP)，SGP中包含工序排序和工厂选择序列，机器选择在解码中通过当前最大完工时间最小化的规则(MCM)确定。MCM 规则如下：从工序序列的第一个工序开始，依次将其安排到使所在工厂当前最大完工
时间最小的机床上。

4）第四种编码包含工序序列、机器序列和工厂序列，为全解空间编码。

本篇推文中所用MA算法采用第四种编码方式，即基因编码包含工序序列、机器序列和工厂序列。

编码方式示意：

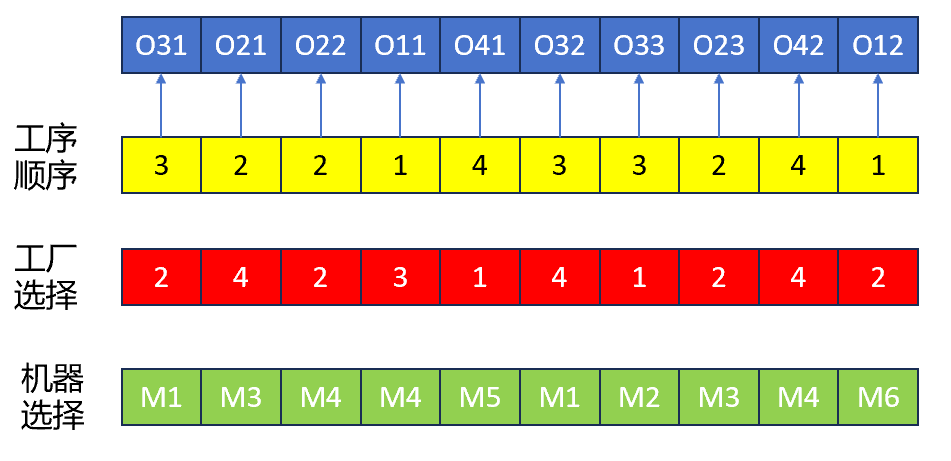
初始化过程中，随机产生每道工序的生产顺序，随后根据工序序列，在每个工序的可选加工工厂集合中随机选择一个加工工厂，最后在对应的加工工厂随机选择可加工的机器。

交叉算子

对工件序列采用基于工序的交叉算子（precedence operation crossover，POX）进行编码，对机器和工厂序列采用一般交叉算子（universial crossover，UC）编码。

function [PopulationTs_new,PopulationFs_new,PopulationMs_new] = CrossOver(PopulationTs,PopulationFs,PopulationMs,P_c,numOfPopulation,numOfTasks,numOfSubTasks)

%1.工厂选择和机器选择序列交叉算子：UX交叉
PopulationFs_new = zeros(numOfPopulation,numOfSubTasks);
PopulationMs_new = zeros(numOfPopulation,numOfSubTasks);
for i = 1:numOfPopulation
    FS_ind = PopulationFs(i,:);
    MS_ind = PopulationMs(i,:);
    K1 = randi(numOfPopulation);
    FSparent_1 = FS_ind;
    FSparent_2 = PopulationFs(K1,:);
    MSparent_1 = MS_ind;
    MSparent_2 = PopulationMs(K1,:);%得到两个父代个体
    P = rand(1);
    if P <= P_c
        K2 = randi(numOfSubTasks);
        random_list = randperm(numOfSubTasks);
        UX_list = random_list(1,1:K2);
        L_UX_list = length(UX_list);
        for k = 1:L_UX_list
            FS_value(1,k) = FSparent_2(1,UX_list(k));
            FSparent_1(1,UX_list(k)) = FS_value(1,k);
            MS_value(1,k) = MSparent_2(1,UX_list(k));
            MSparent_1(1,UX_list(k)) = MS_value(1,k);
        end
        PopulationFs_new(i,:) = FSparent_1;
        PopulationMs_new(i,:) = MSparent_1;
    else
        PopulationFs_new(i,:) = FS_ind;
        PopulationMs_new(i,:) = MS_ind;
    end
end


%2 工序序列交叉算子：POX交叉
PopulationTs_POX = PopulationTs(:,:);
PopulationTs_new = zeros(numOfPopulation,numOfSubTasks);
for n = 1:numOfPopulation
    TS_ind = PopulationTs_POX(n,:);
    TS_K1 = randi(numOfPopulation);
    TSparent_1 = TS_ind;
    TSparent_2 = PopulationTs_POX(TS_K1,:);%得到两个父代个体
    P = rand(1);
    if P <= P_c
        TS_list = randperm(numOfTasks);
        TS_K1 = randi(numOfTasks);
        POX_list1 = TS_list(1,1:TS_K1);
        POX_list2 = TS_list(1,TS_K1 + 1:numOfTasks);
        judge1 = zeros(1,numOfSubTasks);
        judge2 = zeros(1,numOfSubTasks);
        for m = 1:numOfSubTasks
            T1 = TSparent_1(1,m);
            T2 = TSparent_2(1,m);
            A0 = find(POX_list1 == T1);
            B0 = find(POX_list2 == T2);
            A = length(A0);
            B = length(B0);
            if A == 0
                judge1(1,m) = 0;
            else
                judge1(1,m) = 1;
            end
            if B == 0
                judge2(1,m) = 0;
            else
                judge2(1,m) = 1;
            end
        end
        index1 = find(judge1 ~= 0);
        index2 = find(judge2 ~= 0);
        index3 = find(judge1 == 0);
        L1 = length(index1);
        L2 = length(index2);
        child_TS = zeros(1,numOfSubTasks);
        for o = 1:numOfSubTasks
            for q = 1:L1
                TS_value1 = TSparent_1(1,index1(1,q));
                child_TS(1,index1(1,q)) = TS_value1;
            end
            for p = 1:L2
                TS_value2 = TSparent_2(1,index2(1,p));
                child_TS(1,index3(1,p)) = TS_value2;
            end
        end
        PopulationTs_new(n,:) = child_TS;
    else
        PopulationTs_new(n,:) = TS_ind;
    end
end

end