codeforces 935C. Fifa and Fafa（圆）-优快云博客

题意：

给一个半径，两个点求圆过第二个点的最大外切圆，如果第二个点在圆外，直接输出第一个点和半径

题解

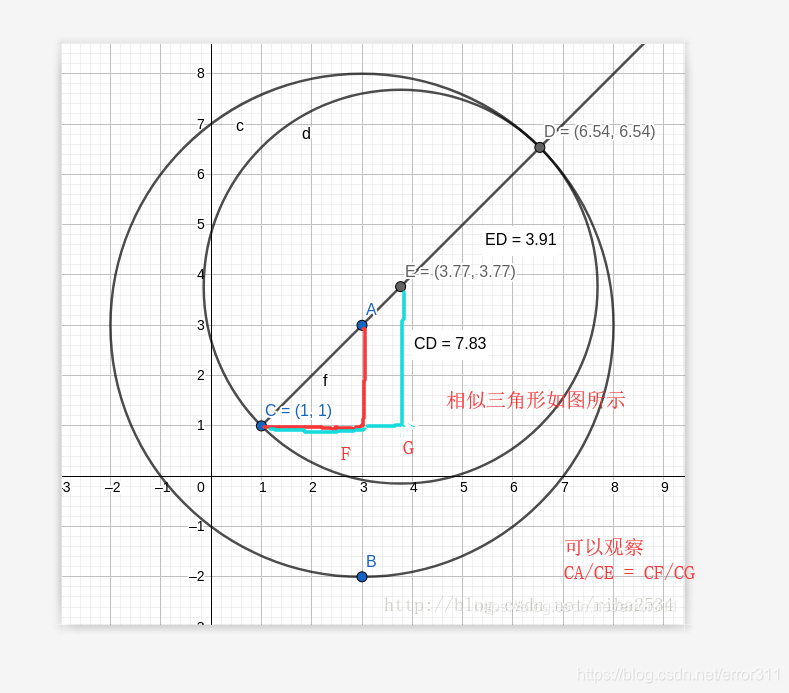
以第二个点为起点，过第二个点做一条射线，交于圆上，长度即为所求直径，然后求出点的坐标

1.圆的方程（x - a） * (x - a) + (y - b) * (y - b) = r *r

2.求根公式 x = ( -b + sqrt(b * b - 4 * a * c)) / 2 * a

我的做法，刚开始需要判断两个横坐标，保证不会除0，wa 1

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const double eps = 1e-4;
int main(){
   double R, x1, y1, x2, y2, xjiao, yjiao;
   cin >> R >> x1 >> y1 >> x2 >> y2;
   if(x1 != x2){
   	double k = (y1 - y2) / (x1 - x2);   // 直线斜率
	   double c = y1 - (k * x1);       // 直线截距
	   double a = 1+k*k;
	   double b = 2*k*c-2*y1*k-2*x1;
	   double d = y1 * y1 + c * c + x1 * x1 - R * R - 2 * y1 * c; 
	   double xjiao1 = (sqrt(b*b-4*a*d) -(b))/(2*a);      // 计算两个交点的横坐标
	   double xjiao2 = (-sqrt(b*b-4*a*d) -(b))/(2*a);
	   if(x1 > x2){
	   	if(xjiao1 > xjiao2){    // 判断圆放在哪边
	   		xjiao = xjiao1;
			}
			else{
				xjiao = xjiao2;
			}
			yjiao = xjiao * k + c;
		}
		else if(x1 < x2){
			if(xjiao1 < xjiao2){
	   		xjiao = xjiao1;
			}
			else{
				xjiao = xjiao2;
			}
			yjiao = xjiao * k + c;
		}
	}
	else{                        // 横坐标相同，比较纵坐标
		xjiao = x1;
		double yjiao1 = R + y1;
		double yjiao2 = -R + y1;
		if(y1 > y2){
			yjiao = max(yjiao1, yjiao2);
		}
		else{
			yjiao = min(yjiao1, yjiao2);
		}
	}
	xjiao = (xjiao + x2) / 2;
	yjiao = (yjiao + y2) / 2;
	double len = sqrt((xjiao-x2) * (xjiao-x2) + (yjiao-y2) * (yjiao-y2));
	if(len > R){                // 第二个点在圆外
		len = R;
		xjiao = x1;yjiao = y1;    // 横纵坐标等于第一个圆的横纵坐标
	}
	printf("%.15lf %.15lf %.15lf\n", xjiao, yjiao, len);
   return 0;
}

别人做法：求坐标时，用相似三角形，简单10倍

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e7+100;
double dis(double x1,double y1,double x2,double y2){ // 计算两点坐标
    return (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2);
}
int main(){
   double r,x1,x2,y1,y2;
   cin>> r >> x1 >> y1 >> x2 >> y2;
   double len = dis(x1,y1,x2,y2);
   if(len >= r*r){                          // 第二个点在圆外，直接输出点坐标和半径
      cout<< x1 << ' ' << y1 << ' ' << r <<endl;
   }
   else if(x1 == x2 && y1 == y2){         // 横纵坐标相等，采用横坐标缩短一半或纵坐标缩短一半
      cout<< x1+r/2 << " " << y1 << ' ' << r/2 <<endl;
   }
   else{
      double Z = sqrt(len);
      double R = (Z+r) / 2;         // 直接求半径，这步好好想想，看图就很简单
      cout<< (x1-x2)*R/Z+x2 << ' ' << (y1-y2)*R/Z+y2 <<' '<< R <<endl;// 相似三角形求点坐标
                                            // 看上图
   }
   return 0;
}