在PostGIS中计算点数据集的最小外包凸多边形等（Calculate the minimum outer convex polygon of a point dataset in PostGIS）

概述

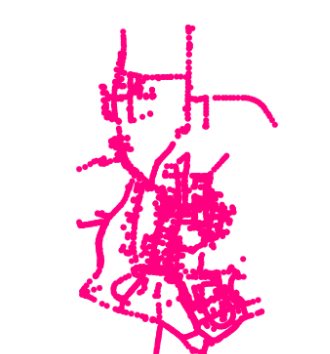
存在点（或线）数据集，其分布情况如下：

现在想要获取该数据的几个外包多边形，主要包含如下三个方法：

方法一

第一种方法，最小外包凸多边形，其结果如下：

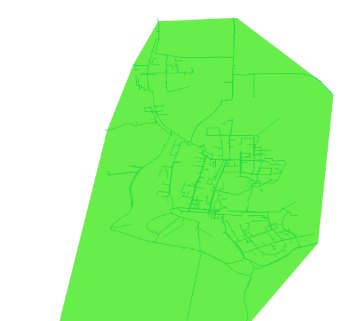
查询语句：ST_ConcaveHull(ST_Collect(geom::geometry),0.2)

方法二

第二种方法，最小外包多边形进行缓冲区：

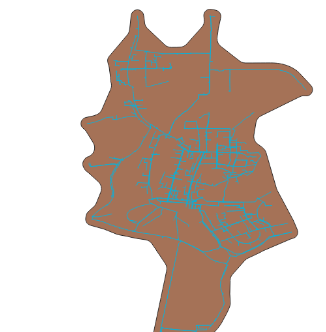
查询语句：ST_BUFFER(ST_BUFFER(ST_ConcaveHull(ST_Collect(geom::geometry),0.001,true),0.0011),-0.0001)

方法三

第三种方法，所有线或者点数据进行缓冲区后取并集：

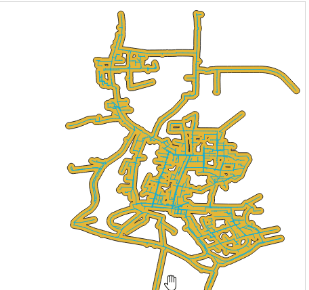
总结

核心是利用ST_BUFFER、ST_Collect、ST_ConcaveHull三个方法，找到合适的参数。

参考

ST_BUFFER详见https://postgis.net/docs/ST_Buffer.html
ST_ConcaveHull详见https://postgis.net/docs/ST_ConcaveHull.html
ST_Collect详见https://postgis.net/docs/ST_Collect.html