数据结构与算法设计-作业1-判断素数个数&约瑟夫环问题

作业1

第一题

设计程序，判断 1~N 之间有多少个素数，要求：N 以程序参数的方式输入

思路

对输入的参数N，需遍历 1~N 之间的每一个数 K，判断其是否为素数，判断方法为检查 K 是否能被 2 到 N-1 之间的任何整数整除，因此需要两重循环。为使代码更为简洁易读，将其拆分为两个函数：

1. 素数判断：prime_find(K) 函数用于判断一个数 K 是否为素数：

   • 如果 K 大于 2，检查 N 是否能被 2 到K-1 之间的任何整数整除。
   • 如果 K 等于 2，直接返回 True（2 是素数）。
   • 如果 K 小于 2，返回 False（1 不是素数）

   def prime_count(N):
       count=0
       ls_prime=[]
       for k in range(1,N+1):
           if prime_find(k): # k是素数
               count+=1
               ls_prime.append(k)
       return count,ls_prime
   

2. 素数计数：定义 prime_count(N) 函数，初始化计数器 count 和存储素数的列表 ls_prime。通过循环遍历从 1 到 N 的每个整数 k，调用 prime_find(k) 判断 k 是否为素数。

   def prime_find(K):
       if K>2:
           for i in range(2,K):
               if K%i==0:
                   return False
           return True
       elif K==2:
           return True
       else:
           return False
   

优化

可以通过以下方式优化这段代码：

1. 改进素数判断：在 prime_find 函数中，只需检查到$\sqrt{k}$，并且可以跳过偶数（除了2），以减少计算量。

   def prime_find(K):
       if K < 2:
           return False
       if K == 2:
           return True
       if K % 2 == 0:
           return False  # 排除偶数
       for i in range(3, int(K**0.5) + 1, 2):  # 只检查奇数
           if K % i == 0:
               return False
       return True
   

2. 使用列表推导：在 prime_count 函数中，可以使用列表推导来简化代码。

   def prime_count(N):
       count = 0
       ls_prime = [k for k in range(2, N + 1) if prime_find(k)]  # 使用列表推导
       count = len(ls_prime)  # 直接获取素数数量
       return count, ls_prime
   

结果

输入不同的N值，检查输出结果：

第二题

约瑟夫环：已知n个人(以编号1，2，3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列。问最后留下的是原来的第几号？(m, n和k为程序输入参数)

思路

使用列表和循环来模拟约瑟夫环的出列过程，逐步将未出列的人移动到队列末尾，以便正确地实现报数和出列的逻辑。特别处理了第一次报数的起始位置。每次出列后，打印当前的队列状态，便于调试和验证。下面是对代码思路的详细解释：

1. 初始化：

   ls = list(range(1, n + 1))
   cnt_delete = 0
   

   • ls 是一个列表，包含从 1 到 n 的所有人，表示每个人的编号。
   • cnt_delete 用于跟踪已经出列的人数，初始值为 0。

2. 主循环：

   while ls:
   

   • 当 ls 不为空时，继续循环，直到所有人都出列。

3. 第一次报数的特殊处理：

   if cnt_delete == 0:
       for i in range(k + m - 2):
           temp = ls.pop(0)
           ls.append(temp)
   

   • 如果是第一次出列（即 cnt_delete 为 0），需要从第 k 个人开始报数。
   • 通过循环 k + m - 2 次，将前面的元素移动到列表的末尾，直到到达第 k 个人并数到第 m 个人。
   • 这里的 k + m - 2 是因为我们需要跳过前 k-1 个人，然后再数 m-1 个。

4. 后续的报数：

   else:
       for i in range(m - 1):
           temp = ls.pop(0)
           ls.append(temp)
   

   • 如果不是第一次出列，则从当前队列的第一个人开始，数到第 m 个人。
   • 通过循环 m - 1 次，将前面的元素移动到列表的末尾，准备出列。

5. 出列操作：

   last_num = ls.pop(0)  # 数到m的人出列
   

   • 计算出列的人的编号，通过 pop(0) 从列表中移除并返回第一个元素（即数到 m 的人）。

6. 更新计数：

   cnt_delete += 1 
   print('出列第{}个人，现在队列为{}'.format(cnt_delete, ls))   # 验证队列是否正确
   

   • 更新已出列的人数，并打印当前出列情况和剩余队列状态。

7. 返回最后一个人：

   return last_num
   

   • 当循环结束时，返回最后出列的人的编号。

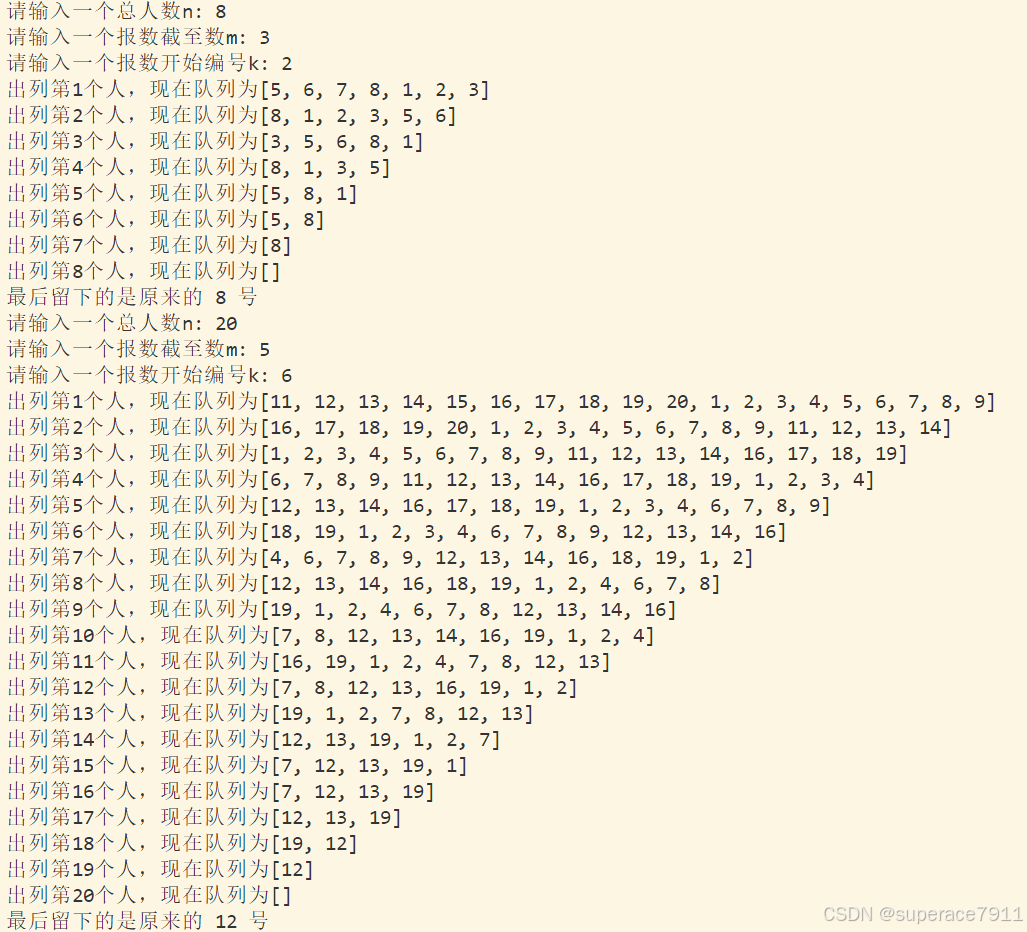
结果