T1
请创建包含100万个数的列表,用本章定义的linear_contains()和binary_contains()函数分别在该列表中查找多个数并计时,演示二分搜索相对于线性搜索的性能优势。
线性搜索按照原始数据结构的顺序遍历空间中的每个元素,直到找到搜索内容或到达数据结构的末尾;
定义如下线性搜索函数,它将遍历数据结构中的每个元素,并检查每个元素是否与所查找的数据相等:
def linear_contains(gene: Gene, key_codon: Codon)-> bool:
for codon in gene:
if codon == key_codon:
return True
return False
acg: Codon = (Nucleotide.A, Nucleotide.C, Nucleotide.G)
gat: Codon = (Nucleotide.G, Nucleotide.A, Nucleotide.T)
print(linear_contains(my_gene, acg))
print(linear_contains(my_gene, gat))
二分搜索的原理:查看一定范围内有序元素的中间位置的元素,将其与所查找的元素进行比较,根据比较结果将搜索范围缩小一半,然后重复上述过程。时间复杂度为O(logn),优于顺序搜索的O(n);
二分搜索需要对有序的数据结构才能进行搜索。
def binary_contains(gene: Gene, key_codon: Codon)-> bool:
low: int = 0
high: int = len(gene)– 1
while low <= high:
# while there is still a search space
mid: int = (low + high) // 2
if gene[mid] < key_codon:
low = mid + 1
elif gene[mid] > key_codon:
high = mid – 1
else:
return True
return False
# 用一份基因数据和密码子运行函数(先进行排序)。
my_sorted_gene: Gene = sorted(my_gene)
print(binary_contains(my_sorted_gene, acg))
print(binary_contains(my_sorted_gene, gat))
思路
使用不同的查找数量进行测试,并记录每次查找的耗时:
# 创建包含100万个数的列表
data = list(range(1000000))
# 定义不同的查找数量
search_counts = [10, 100, 1000, 5000, 10000]
测试线性搜索和二分搜索的耗时:
for count in search_counts:
keys_to_search = random.sample(data, count)
# 线性搜索计时
start_time = time.time()
for key in keys_to_search:
linear_contains(data, key)
end_time = time.time()
print(f"线性搜索查找 {count} 个数耗时: {end_time - start_time:.6f} 秒")
# 二分搜索计时
# 确保数据已排序
sorted_data = sorted(data)
start_time = time.time()
for key in keys_to_search:
binary_contains(sorted_data, key)
end_time = time.time()
print(f"二分搜索查找 {count} 个数耗时: {end_time - start_time:.6f} 秒")
完整代码见assignment6_1.py
结果
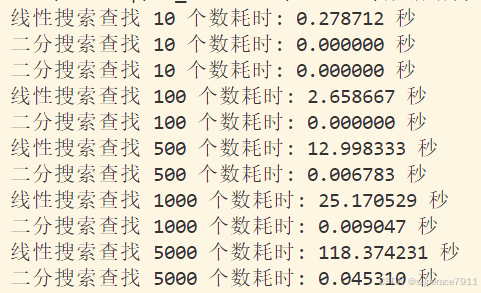
打印结果如下:
分析
从输出结果来看, 线性搜索的耗时随着查找数量的增加而显著增加,这是由于其线性时间复杂度决定的。而二分搜索由于其对数时间复杂度,在处理大数据集时非常高效,耗时几乎可以忽略不计。
二分搜索的耗时有时候显示为0秒,分析原因如下:
-
Python 的时间精度:在 Python 中,
time.time()函数的精度有限,对于非常短的时间间隔(如二分搜索的耗时),可能会显示为 0 秒。这并不意味着二分搜索真的耗时为 0,而是因为时间间隔太短,无法被精确测量。 -
排序耗时:在每次进行二分搜索之前,代码都会对数据进行排序。虽然排序的耗时没有单独计算,但由于数据集已经是有序的,排序操作的耗时可以忽略不计。
T2
给dfs()、bfs()和astar()添加计数器,以便查看它们对同一迷宫进行搜索时遍历的状态数量。请针对100个不同的迷宫进行搜索并计数,以获得统计学上有效的结论。
代码实现
修改generic_search.py,给每一个算法添加计数器如下(以dfs()为例):
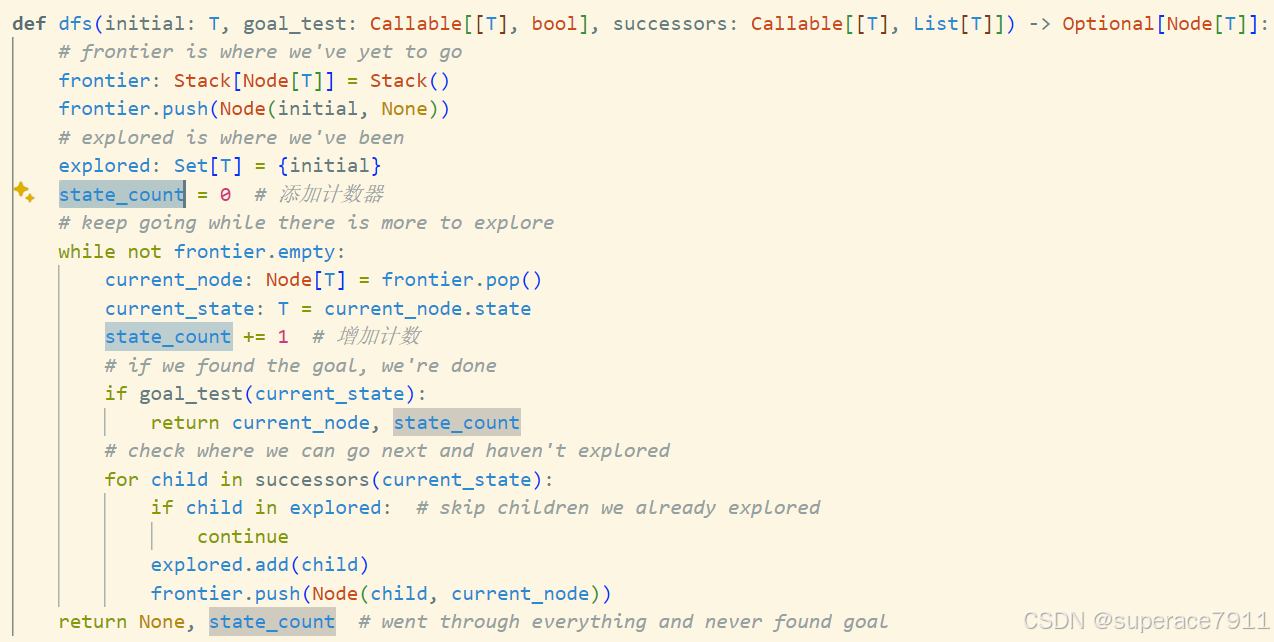
使用脚本test_count.py测试 DFS、BFS 和 A* 三种搜索算法在 100 个不同迷宫中的表现,并统计每种算法遍历的状态数量。
定义测试函数,用字典results存储每种算法在100个迷宫中遍历的状态数量:
def test_search_algorithms():
results = {
"DFS": [],
"BFS": [],
"A*": []
}
将 results 字典转换为一个DataFrame results_df。
使用 describe() 方法显示 DataFrame 的描述性统计信息,包括计数、平均值、标准差、最小值、四分位数和最大值。
results_df = pd.DataFrame(results)
print(results_df.describe())
结果

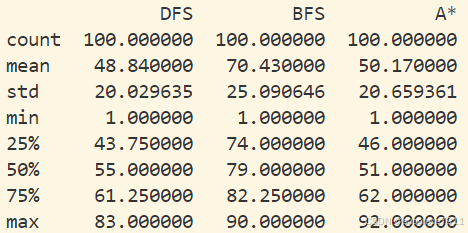
从输出结果来看,我们可以对 DFS、BFS 和 A* 搜索算法在 100 个迷宫中的表现进行分析:
分析
-
平均遍历状态数量:
- BFS 的平均遍历状态数量最高,为 70.43。
- A* 的平均遍历状态数量为 50.17,略高于 DFS 的 48.84。
- 这表明 BFS 在这些迷宫中通常需要遍历更多的状态才能找到目标,而 DFS 和 A* 的表现相对接近。
-
标准差:
- BFS 的标准差最高,为 25.09,表明其遍历状态数量的波动较大。
- DFS 和 A* 的标准差相对较低,分别为 20.03 和 20.66,表明它们的遍历状态数量较为稳定。
-
最小值和最大值:
- 所有算法的最小遍历状态数量都是 1,表明在某些情况下,目标状态非常接近起始状态。
- 最大遍历状态数量方面,A* 的最大值为 92,略高于 BFS 的 90 和 DFS 的 83。
-
百分位数:
- 从 25%、50% 和 75% 百分位数来看,BFS 的遍历状态数量在大多数情况下都高于 DFS 和 A*。
- A* 的 50% 和 75% 百分位数略高于 DFS,表明在大多数情况下,A* 的遍历状态数量略多于 DFS。
结论
- BFS: 在这些迷宫中,BFS 通常需要遍历更多的状态才能找到目标,且其遍历状态数量的波动较大。
- DFS: DFS 的遍历状态数量相对较少且稳定。
- A*: A* 的表现介于 DFS 和 BFS 之间,遍历状态数量略多于 DFS,但少于 BFS,且其波动也较小。
总体而言,DFS 和 A* 在这些迷宫中的表现较为接近,而 BFS 通常需要遍历更多的状态。
理论分析
在分析 DFS、BFS 和 A* 搜索算法在迷宫搜索中的表现时,需要考虑每种算法的特性及其在不同情况下的表现。
深度优先搜索 (DFS)
- 特点: DFS 是一种盲目搜索算法,它沿着一个路径一直走到底,直到找到目标或遇到死胡同,然后回溯并尝试另一条路径。
- 时间复杂度: 在最坏情况下,DFS 的时间复杂度为 O(b^d),其中 b 是每个节点的分支因子,d 是目标节点的深度。
- 空间复杂度: DFS 的空间复杂度为 O(d),因为它只需要存储当前路径上的节点。
- 优点: 在路径较短或目标较近的情况下,DFS 可能会很快找到目标。
- 缺点: 在路径较长或有很多死胡同的情况下,DFS 可能会遍历大量无关节点,导致效率低下。
广度优先搜索 (BFS)
- 特点: BFS 是一种盲目搜索算法,它逐层遍历节点,直到找到目标。
- 时间复杂度: 在最坏情况下,BFS 的时间复杂度为 O(b^d),其中 b 是每个节点的分支因子,d 是目标节点的深度。
- 空间复杂度: BFS 的空间复杂度为 O(b^d),因为它需要存储每一层的所有节点。
- 优点: BFS 保证找到最短路径(如果所有边的权重相同)。
- 缺点: BFS 需要大量内存来存储每一层的节点,尤其是在分支因子较大或目标节点较深的情况下。
A* 搜索
- 特点: A* 是一种启发式搜索算法,它结合了 DFS 和 BFS 的优点,通过估计函数(启发式)来指导搜索方向。
- 时间复杂度: 在最坏情况下,A* 的时间复杂度为 O(b^d),其中 b 是每个节点的分支因子,d 是目标节点的深度。
- 空间复杂度: A* 的空间复杂度为 O(b^d),因为它需要存储所有已生成的节点。
- 优点: A* 使用启发式函数来估计从当前节点到目标节点的代价,从而更有效地找到最短路径。
- 缺点: A* 的性能依赖于启发式函数的质量。如果启发式函数不准确,A* 可能会退化为 BFS。
理论分析结果
-
DFS:
- 在路径较短或目标较近的情况下,DFS 可能会很快找到目标。
- 在路径较长或有很多死胡同的情况下,DFS 可能会遍历大量无关节点,导致效率低下。
- 由于 DFS 只需要存储当前路径上的节点,其空间复杂度较低。
-
BFS:
- BFS 保证找到最短路径,但需要大量内存来存储每一层的节点。
- 在分支因子较大或目标节点较深的情况下,BFS 的空间复杂度较高。
- BFS 的遍历状态数量通常较多,因为它需要逐层遍历所有节点。
-
A*:
- A* 使用启发式函数来指导搜索方向,通常比 DFS 和 BFS 更有效。
- A* 的性能依赖于启发式函数的质量。如果启发式函数准确,A* 可以更快找到最短路径。
- A* 的空间复杂度较高,因为它需要存储所有已生成的节点。
实验结果与理论分析的对比
- DFS 的平均遍历状态数量较少,且标准差较小,表明其遍历状态数量较为稳定。这与理论分析一致,因为 DFS 只需要存储当前路径上的节点。
- BFS 的平均遍历状态数量最高,且标准差最大,表明其遍历状态数量波动较大。这与理论分析一致,因为 BFS 需要逐层遍历所有节点,导致遍历状态数量较多。
- A* 的平均遍历状态数量介于 DFS 和 BFS 之间,且标准差较小,表明其遍历状态数量较为稳定。这与理论分析一致,因为 A* 使用启发式函数来指导搜索方向,通常比 DFS 和 BFS 更有效。
总体而言,实验结果与理论分析一致,验证了不同搜索算法在迷宫搜索中的表现。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








