【JZOJ3294】【BZOJ4417】【luoguP3990】超级跳马

矩阵乘法优化DP算法

最新推荐文章于 2020-01-03 21:36:04 发布

原创最新推荐文章于 2020-01-03 21:36:04 发布 · 371 阅读

1 ·

CC 4.0 BY-SA版权

模拟赛同时被 3 个专栏收录

240 篇文章

订阅专栏

65 篇文章

订阅专栏

矩阵乘法

10 篇文章

订阅专栏

本文探讨了一种利用矩阵乘法优化动态规划(DP)算法的方法，通过将DP过程转化为矩阵运算，实现了从O(nm^2)到O(nm)的时间复杂度优化。文章详细解释了如何将奇数列和偶数列的DP状态转换为矩阵形式，并通过矩阵乘法进行高效计算。

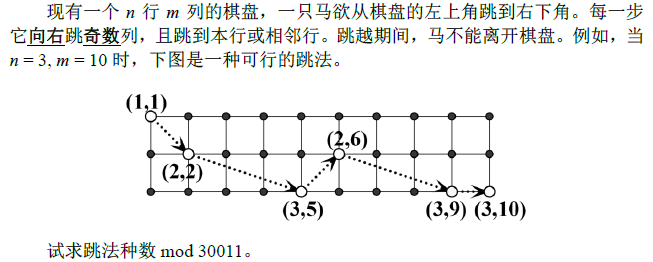
description

analysis

矩阵乘法好题
最朴素的 $10 p t s$ 的 $f [i] [j]$ 容易 $D P$ ，但是是 $O(nm^2)$ 的复杂度
于是把 $10$ 分的 $D P$ 写出来，就可以知道 $f [i] [j] + = f [k] [l]$ 的部分可以搞前缀和优化， $O (n m)$ 有 $50 p t s$
这个要先弄懂才可以继续搞矩乘
可以分成奇数列和偶数列分别 $D P$ ，设 $f [i], g [i]$ 分别表示某奇数列的第 $i$ 行和偶数列的第 $i$ 行的方案数的前缀和
$f [i]$ 和 $g [i]$ 都要加上第 $i$ 行前面与他奇偶性相同的方案数方便转移，具体见代码
于是 $f [i] = g [i - 1] + g [i] + g [i + 1], g [i] = f [i - 1] + f [i] + f [i + 1]$ （注意边界的两个点），可以矩乘优化了
具体就是，初始矩阵写成前一半是 $f [1 . . n]$ ，后一半是 $g [1 . . n]$
想办法矩乘转移到 $(g [1 . . n], f ’ [1 . . n])$ ，这里举 $n = 3$ 的例子
$(1, 0, 0, 1, 1, 0) * F = (1, 1, 0, 3, 2, 1)$ ，因为打表发现 $(1,1,2...0,1,2...0,0,1...)\left( \begin{matrix} 1,1,2...\\ 0,1,2... \\ 0,0,1... \end{matrix} \right)$ ，这个 $3$ 加上了前面的那个 $1$
于是由 $(f [i - 1], f [i], f [i + 1], g [i - 1], g [i], g [i + 1]) * F = (g [i - 1], g [i], g [i + 1], f ’ [i - 1], f ’ [i], f ’ [i + 1])$ 推矩阵
注意 $f [i] = g [i - 1] + g [i] + g [i + 1]$ ，推出来大概就是 $(0,0,0,1,0,00,0,0,0,1,00,0,0,0,0,11,0,0,1,1,00,1,0,1,1,10,0,1,0,1,1)\left( \begin{matrix} 0,0,0,1,0,0\\ 0,0,0,0,1,0 \\ 0,0,0,0,0,1\\ 1,0,0,1,1,0\\ 0,1,0,1,1,1\\ 0,0,1,0,1,1\\ \end{matrix} \right)$
$n = 10$ 的矩阵长这样

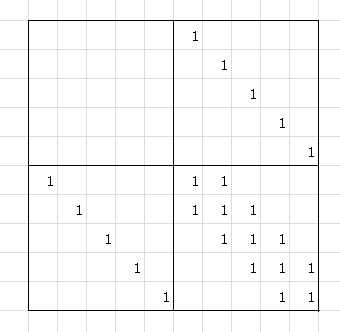
于是就可以直接上矩乘搞了，答案就为最后两位的和

code

#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 55
#define mod 30011
#define ll long long
#define fo(i,a,b) for (ll i=a;i<=b;++i)
#define fd(i,a,b) for (ll ia=;i>=b;--i)

using namespace std;

ll n,m;

struct matrix
{
	ll a[MAXN<<1][MAXN<<1],n,m;
	matrix(){memset(a,0,sizeof(a)),n=m=0;}
	matrix(ll x,ll y){memset(a,0,sizeof(a)),n=x,m=y;}
}f,ans,ans1,f1;
inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
inline matrix operator*(matrix a,matrix b)
{
	matrix c(a.n,b.m);
	fo(i,1,a.n)
	fo(j,1,b.m)
	fo(k,1,a.m)(c.a[i][j]+=a.a[i][k]*b.a[k][j])%=mod;
	return c;
}
inline matrix pow(matrix x,ll y)
{
	matrix z=x;
	while (y)
	{
		if (y&1)z=z*x;
		y>>=1,x=x*x;
	}
	return z;
}
int main()
{
	n=read(),m=read();
	ans=ans1=matrix(1,n<<1),f=f1=matrix(n<<1,n<<1);
	ans.a[1][1]=ans.a[1][n+1]=ans.a[1][n+2]=f.a[n+1][n+1]=1;
	fo(i,n+2,n<<1)f.a[i][i]=f.a[i-1][i]=f.a[i][i-1]=1;
	fo(i,1,n)f.a[i][n+i]=f.a[n+i][i]=1;
	f1=pow(f,m-3),ans1=ans*f1;
	printf("%lld\n",(ans1.a[1][n-1]+ans1.a[1][n])%mod);
	return 0;
}