导弹动力学模型:
import numpy as np
from math import *
class Missile:
# def __init__(self,v,theta,phi_v,x,y,z):
# self.v = v
# self.theta = theta
# self.phi_v = phi_v
# self.x = x
# self.y = y
# self.z = z
def dery(self,Y,t,Var,U):
ax = U[0]
ay = U[1]
az = U[2]
v = Y[0]
theta = Y[1]
psi_v = Y[2]
dv = ax
dtheta = ay/v
dpsi_v = -az/(v*cos(theta))
dx = v*cos(theta)*cos(psi_v)
dy = v*sin(theta)
dz = -v*cos(theta)*sin(psi_v)
self.vx = dx
self.vy = dy
self.vz = dz
return np.array([dv,dtheta,dpsi_v,dx,dy,dz],dtype=float)
def RungeKutta4(self,Y,h,tn,Var,U):
k1 = self.dery(Y, tn,Var,U)
k2 = self.dery(Y + h*0.5*k1,tn + 0.5 * h,Var,U)
k3 = self.dery(Y + h*0.5*k2,tn + 0.5 * h,Var,U)
k4 = self.dery(Y + h*k3, tn + h, Var,U)
# 返回一次迭代后的y值
Y = Y + h/ 6.0 *(k1 + 2 * k2 + 2 * k3 + k4)
return Y
目标动力学模型:
import numpy as np
from math import *
class Target:
# def __init__(self,v,theta,phi_v,x,y,z):
# self.v = v
# self.theta = theta
# self.phi_v = phi_v
# self.x = x
# self.y = y
# self.z = z
def dery(self,Y,t,Var,U):
ax = U[0]
ay = U[1]
az = U[2]
v = Y[0]
theta = Y[1]
psi_v = Y[2]
dv = ax
dtheta = ay/v
dpsi_v = -az/(v*cos(theta))
dx = v*cos(theta)*cos(psi_v)
dy = v*sin(theta)
dz = -v*cos(theta)*sin(psi_v)
self.vx = dx
self.vy = dy
self.vz = dz
return np.array([dv,dtheta,dpsi_v,dx,dy,dz],dtype=float)
def RungeKutta4(self,Y,h,tn,Var,U):
k1 = self.dery(Y, tn,Var,U)
k2 = self.dery(Y + h*0.5*k1,tn + 0.5 * h,Var,U)
k3 = self.dery(Y + h*0.5*k2,tn + 0.5 * h,Var,U)
k4 = self.dery(Y + h*k3, tn + h, Var,U)
# 返回一次迭代后的y值
Y = Y + h/ 6.0 *(k1 + 2 * k2 + 2 * k3 + k4)
return Y
仿真结果:导弹准确拦截空中目标
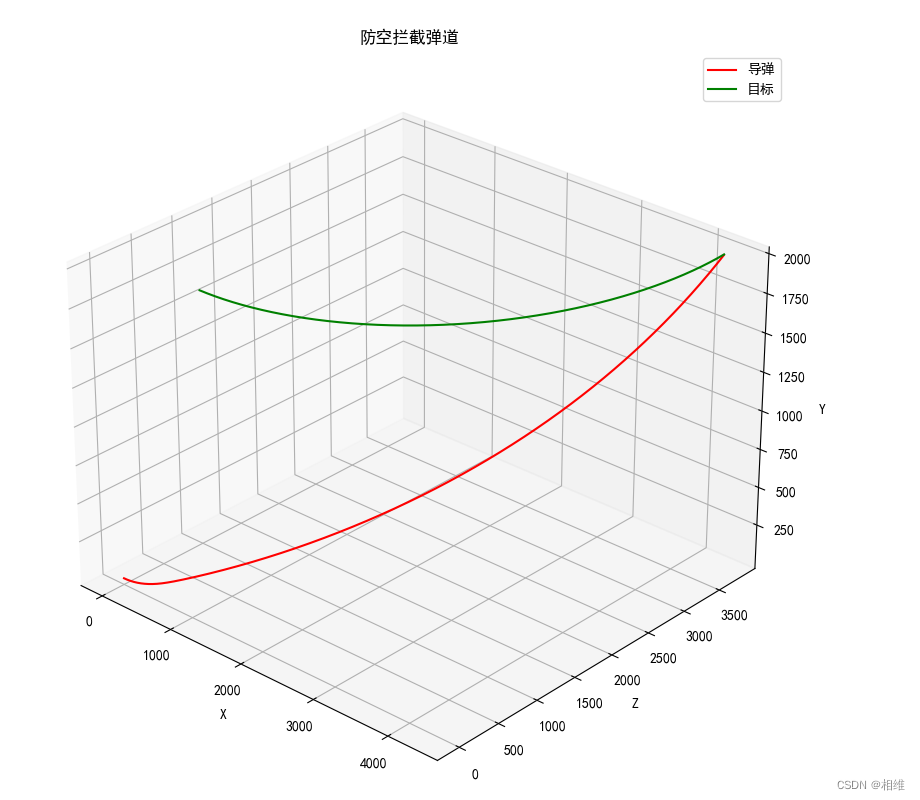
专业制导控制仿真+qq1763053463





















 5049
5049

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










