10.4.3 堆排序

相关定义

• 堆的定义
  堆是满足 下列性质 的序列。
  { r₁ , r₂ , … , r_n }
  r_i <= r_2i 且 r_i <= r_2i+1
  或者
  r_i >= r_2i 且 r_i >= r_2i+1
  这样的序列，叫作 堆。
  
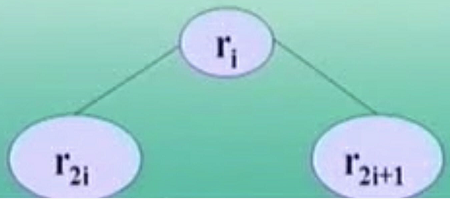
  用 二叉树 表示，就是 一个结点的关键字 一定比 它两个子树根结点的关键字 小或者大。
  堆顶 是其所在序列的 最小值或者最大值 。
  堆排序 就是利用 堆的特性 对记录序列进行排序的排序方法。

• 筛选
  对一棵 左右子树均为堆的完全二叉树 ，调整根结点使 整个二叉树 为堆。

• 大顶堆：每个 父结点的关键字 都比 其两个子结点的关键字 要大。
  小顶堆：每个 父结点的关键字 都比其 两个子结点的关键字 要小。

堆排序算法

typedef SqList HeapType;

// 筛选算法
void HeapAdjust(HeapType &H, int s, int m)
{
	// 已知 H.r[s .. m] 中记录的关键字除 H.r[s].key 之外均满足堆的定义，本函数调整
	// H.r[s] 的关键字，使 H.r[s .. m] 称为一个大顶堆（对其中记录的关键字而言）
	rc = H.r[s];
	for(j = 2*s;
		j <= m;
		j *= 2 )
	{
		if(j<m && LT(H.r[j].key, H.r[j+1].key))
		{
			j++;
		}
		if(!LT(rc.key, H.r[j].key))
		{
			// rc 的关键字大，不需要再向下遍历，退出循环
			break;
		}
		// r[j] 处的关键字较大，先放到堆顶去，下一轮循环找机会填这个空
		H.r[s] = H.r[j];
		// 空位由 s 变为 j
		s = j;
	}
	H.r[s] = rc;
}

void HeapSort(HeapType &H)
{
	// 对顺序表 H 进行堆排序，把 H.r[1 .. H.length] 建成大顶堆
	for(i = H.length/2;
		i > 0;
		i-- )
	{
		HeapAdjust(H, i, H.length);
	}
	for(i = H.length;
		i > 1;
		i-- )
	{
		// 将堆顶记录和当前未经排序子序列 Hr[1 .. i] 中最后一个记录相互交换
		Swap(H.r[1], H.r[i]); 
		// 将 H.r[1 .. i-1] 重新调整为大顶堆
		HeapAdjust(H, 1, i-1);
	}
} // 该算法完成后整个记录序列变成一个按关键字递增序列

堆排序时空间性能分析

• 堆排序的时间复杂度
  简单选择排序 O( n² )
  堆排序 O( nlogn )
  
  

• 空间上只需要一个单位的辅助空间。用于记录交换。