7.5.2关键路径

• AOV - 网
  顶点 表示 活动，activity on vertex
  弧 表示 活动间的优先关系
  此类有向图叫作 AOV - 网

• AOE - 网
  顶点 表示 事件，activity on edge
  边 表示 活动
  此类带权、有向的无环图（权表示活动的持续时间）。

• AOE - 网 一般用来估算一个工程的完成时间

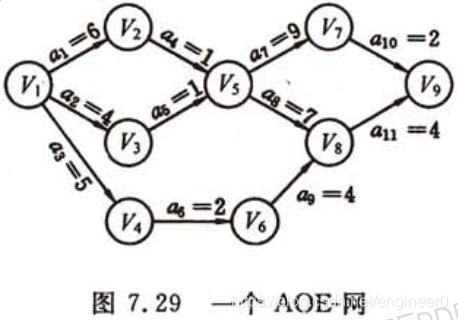
• AOE -网 示例
  下图是一个有 11 项活动 的 AOE - 网。其中有 9 个事件 v₁ , v₂ , … , v₉。
  每个事件 表示 在它之前的活动已经完成，在它之后的活动可以开始。
  如 v₁ 表示整个工程开始，
  v₉ 表示整个工程结束，
  v₅ 表示 a₄ 和 a₅ 已经完成，a₇ 和 a₈ 可以开始。
  与每个活动相联系的数 是 执行该活动所需的时间（弧的权值）。
  

• 源点和汇点
  源点：由于整个工程只有一个 开始点 和 一个 完成点，故正常情况（无环）下，网中只有一个入度为 0 的点，此点为 源点；
  汇点：只有一个 出度 为 0 的点，此点叫作汇点。

• AOE - 网 研究的主要问题
  1、 完成整个工程至少需要多少 时间
  2、哪些活动是影响 工程进度 的 关键

• 关键路径
  AOE - 网 中有些活动是可以并行进行，所以 完成工程的最短时间 是从开始点到完成点的最长的路径长度（指路径上个活动持续时间之和，不是弧的数目）。
  路径长度最长的路径 叫作 关键路径 。

• 事件 v_i 的最早发生时间
  假设开始点是 v₁ ，从 v₁ 到 v_i 的 最长路径长度 叫作 事件 v_i 的最早发生时间。

• 活动 的 最早开始时间 e(i)
  某个 顶点 v_i （表示某个事件）的 最早开始时间 决定了所有以 v_i 为尾的弧 所表示的活动的最早开始时间 。此用 e(i) 来表示。

• 活动的最迟开始时间 l(i)
  在 不推迟整个工程完成 的前提下，活动 a_i 最迟必须开始进行的时间。

• 活动的时间余量
  某个活动的 最迟开始时间 l(i) 和 最早开始时间 e(i) 的差值。

• 关键活动
  最早活动时间 和 最迟活动时间 相同，即该活动的 时间余量 为 0 ，l(i) == e(i) 的活动。

• 关键路径
  路径上的活动 都是 关键活动，
  提前完成 非关键活动 并 不能加快工程的进度。

• 分析关键路径的目的 是辨别哪些是关键活动，以争取提高关键活动的工效，缩短整个工期。
  如下图中的网，从 v₁ 到 v₉ 的 最长路径 是 （ v₁ , v₂ , v₅ , v₈ , v₉ ），路径长度 是 18，即 v₉ 的最早发生时间是 18
  活动 a₆ 的最早开始时间是 5，最迟开始时间是 8，这表明 a₆ 推迟 3 天开始或者延迟3天完成，都不会影响整个工程的完成。
  

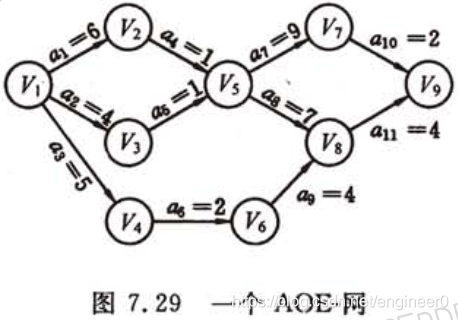
如何寻找关键活动

• 寻找 e(i) = l(i) 的活动，那么就要求 AOE - 网中活动的 e(i) 和 l(i)；
  首先求得事件的 最早发生时间 ve(i) 和 最迟发生时间 vl(j)
  活动 a_i 由弧 <j, k> 表示，其 持续时间 记为 dut( <j ,k> )
  则有如下关系：
  e( i ) = ve( j )
  l( i ) = vl( k ) - dut( <j, k> )
  求 ve( j ) 和 vl( j ) 分两步进行
  
  上面两步递推公式的计算必须分别在 拓补有序 和 逆拓补有序 的前提下进行。
  也就是说，ve( j-1 ) 必须在 v_j 的 所有前驱的最早发生时间 求得之后才能确定；
  vl( j-1 ) 则必须在 v_j 的 所有后继的最迟发生时间 求得之后才能确定

求关键路径的算法（文字描述）

• 1、输入 e 条弧 <j, k>，建立 AOE - 网 存储结构。
• 2、从源点 v₀ 出发，令 ve[0] = 0；
  按 拓补有序 求其余 各顶点的最早发生时间 ve[i]（1 ~ n-1）
  如果 得到的拓补有序序列中顶点个数 小于 网中顶点数 v，则说明网中存在环，不能求关键路径，算法终止；否则执行步骤（3）。
• 3、从汇点 v_n 出发，令 vl[n-1] = ve[n-1]，按逆拓补有序求其余各顶点的最迟发生时间 vl[i]（2 ~ n-2）。
• 4、根据各顶点的 ve 和 vl 值，求每条弧 s 的 最早开始时间 e(s) 和 最迟开始时间 l(s)。若某条弧满足条件 e(s) = l(s) ，则为关键活动。

---