7.3.1深度优先搜索

定义

• 类似于树的先根遍历，但访问结点前要判断此节点是否被访问过。
• 深度优先遍历过程
  假设初始状态是一个无向图中所有的结点都未被访问，
  从图中某个顶点 v 出发，访问此顶点，
  然后依次对 v 的 未被访问的邻接点 进行 深度优先遍历图（递归），直至图中所有和 v 有路径相通的顶点都被访问到；
  若此时图中还有顶点未被访问，则另选图中未被访问的顶点为始点，重复上述过程，直至所有的顶点都被访问过。
  （对每个结点来说都是一个递归的过程）

图例

• 对 G₄ 进行 深度优先遍历
  
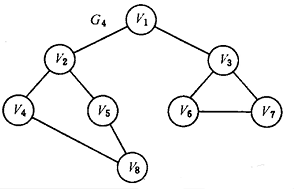
  假设从顶点 v₁ 出发进行搜索，
  在访问了顶点 v₁ 之后，选择邻接点 v₂。
  v₂ 未曾被访问，从 v₂ 出发进行搜索。
  以此类推，依次访问 v₄ ，v₈ ，v₅ 。
  由于 v₅ 的邻接点都已被访问过 ，因此从 v₅ 返回 v₈ 。同理依次返回到 v₄ ，v₂ ，v₁ 。
  v₁ 的另一个邻接点 v₃ 未被访问，接下来依次访问 v₃ ，v₆ ，v₇。

• G₄ 深度优先搜索的顶点访问序列
  v₁ -> v₂ -> v₄ -> v₈ -> v₅ -> v₃ -> v₆ -> v₇

• 在访问过程中，为了区分顶点是否已经被访问，需附设访问标志数组 visited [ 0 … n-1 ]

深度优先遍历算法

Boolean visited[MAX]; // 访问标志数组
Status (*VisitFunc)(int v); // 函数变量

// 对 图G 做深度优先遍历
void DFSTraverse(Graph G, Status (*Visit)(int v))
{
	VisitFunc = visit;
	// 访问标志数组初始化
	for(v=0; v<G.vexnum; v++)
	{
		visited[v] = FALSE;
	}
	// 防止是非连通图，遍历所有结点
	for(v=0; v<G.vexnum; v++)
	{
		if(!visited[v])
		{
			DFS(G, v);
		}
	}
}

// 从 图G 的第 v 个顶点出发，递归深度优先遍历图 G
void DFS(Graph G, int v)
{
	visited[v] = TRUE;
	VisitFunc(v);
	for(w=FirstAdjVex(G, v)
			w>=0;
			w=NextAdjVex(G, v, w))
	{
		if(!visited[w])
		{
			DFS(G, w);
		}
	}
}

• 遍历图的实质
  对每个顶点查找其邻接点的过程，
• 耗费的时间取决于所采用的存储结构
  当用二维数组表示邻接矩阵作为图的存储结构时，查找每个顶点的邻接点所需时间是 O( n² )
  采用邻接表存储结构时，查找每个顶点的邻接点所需时间为 O( e )，深度优先搜索遍历图的时间复杂度为 O( n + e )。访问过的顶点不会再访问，因此访问顶点本身的时间复杂度为 O(n)