7.3.2 广度优先搜索

最新推荐文章于 2025-05-18 09:24:23 发布

原创最新推荐文章于 2025-05-18 09:24:23 发布 · 785 阅读

0 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

58 篇文章

订阅专栏

广度优先搜索遍历 类似于 树的按层次遍历的过程
广度优先搜索遍历过程
1、假设从图中某顶点 v 出发，在访问了 v 之后依次访问 v 的各个未曾访问过的邻接点，
2、然后分别从这些邻接点出发，依次访问它们的邻接点。使得先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问。
3、完毕后若图中还有未被访问的顶点，那么另选一个未曾被访问的顶点作起始点，重复上述过程直到所有的顶点都被访问。
广度优先搜索遍历过程总结
是以某个顶点 v 为起始点，由近至远，依次访问和 v 有路径相通且路径长度为 1 ，2 ，… 的顶点
和深度优先搜索类似，广度优先搜索过程中也需要一个访问标志数组。
利用队列来存储已被访问的路径长度为 1 ，2 ，… 的顶点，实现广度优先搜索的按层次遍历。

广度优先搜索图例

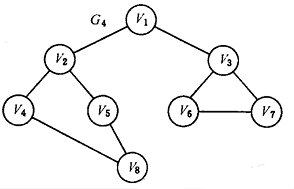
在这里插入图片描述

广度优先搜索访问序列为
v₁ -> v₂ -> v₃ -> v₄ -> v₅ -> v₆ -> v₇ -> v₈

代码算法

void BFSTraverse(Graph G, Status (*Visit)(int v))
{
	for(v=0; v<G.vexnum; v++)
	{
		visited[v] = FALSE;
	}
	InitQueue(Q);
	for(v=0; v<G.vexnum; v++)
	{
		if(!visited[v])
		{
			visited[v] = TRUE;
			Visit(v);
			EnQueue(Q, v);
			while(!QueueEmpty(Q))
			{
				DeQueue(Q, u);
				for(w=FirstAdjVex(G, u);
						w>=0;
						w=NextAdjVex(G, u, w);)
				{
					if(!visited[w])
					{
						visited[w] = TRUE;
						Visit(w);
						EnQueue(Q, w);
					}
				}
			}
		}
	}
}