带授权关键词搜索的公钥加密

带授权关键词搜索的公钥加密

江鹏1,2(B)，穆毅2,郭富春2,和温巧燕1
1网络与交换技术国家重点实验室，北京邮电大学，北京100876，中国 wqy@bupt.edu.cn
2计算机与信息安全研究中心，计算与信息技术学院，伍伦贡大学，伍伦贡，新南威尔士州2522，澳大利亚{pj688,ymu,fuchun}@uow.edu.au

摘要

带关键词搜索的公钥加密（PEKS）为用户识别特定加密数据提供了一种优雅的机制。PEKS在保护数据不被泄露的同时，使其具备可搜索性。本文提出一种新的密码学原语，称为带授权关键词搜索的公钥加密（PEAKS）。在PEAKS中，关键词使用一个公钥进行加密，没有对应私钥的用户需要从授权机构获得授权后才能进行关键词搜索。我们提出了一个具体的PEAKS构造，允许授权机构授权用户搜索不同的关键词集。所提出的方案具有常数大小的授权令牌，与关键词集的大小无关，从而显著降低了带宽消耗。该特性使得当出于安全性考虑需要频繁随时间更新授权令牌时，我们的PEAKS尤为实用。本文还形式化证明了该方案在抵抗选择关键词攻击下的语义安全性和陷门不可伪造性。

关键词 ：加密关键词搜索 · 公钥加密 · 低带宽

1 引言

随着大数据时代的到来，高效的数据检索和数据挖掘变得更加困难。一种可行的方法是用户下载并解密所有加密数据，以查找其感兴趣的内容。该方法会消耗大量的通信带宽和计算资源。另一种方法是用户使用服务器，利用私钥执行解密操作并返回目标数据。然而，这种方法可能损害数据隐私。

博恩等人[5]提出了公钥加密与关键词搜索（PEKS）的概念，以实现对加密数据的搜索。PEKS解决了上述问题，并避免了对称可搜索加密中复杂的密钥管理[22]。

在PEKS中，发送方上传带有可搜索密文的加密数据。用户向服务器生成与某个关键词相关的陷门以进行搜索。当陷门中的关键词与可搜索密文中的关键词相同时，服务器将相应的加密数据返回给接收者。

使用特定用户的公钥生成PEKS的可搜索密文，且仅有一个实体（私钥持有者）能够进行搜索。在企业场景中，许多员工需要基于企业的公钥对加密关键词拥有搜索权限。通过PEKS，每个员工都必须获得企业的私钥以生成陷门。这种简单的解决方案容易导致密钥滥用，并存在局限性。例如，每个员工可能处于不同的访问级别，只能搜索某些关键词。一种可行的解决方案是授权机构（即管理者）保管企业的私钥，并向每位员工授权特定的搜索权限。授权机构为每位员工设置一个授权关键词集，员工只能搜索该授权关键词集中的关键词。

一种可能的方案是允许授权机构为每个授权关键词生成授权令牌。出于安全考虑，每个授权令牌仅在较短的时间间隔内有效，当时间到期时，授权机构需要为在线员工重新授权令牌。此过程需要在每个新的时间间隔内对每位在线员工重复执行。不幸的是，这种方法可能会消耗大量带宽。如何高效地授权关键词搜索成为一个亟需解决的重要问题。

贡献

本文的贡献有两方面。首先，我们提出了一种名为带授权关键词搜索的公钥加密（PEAKS）的新概念。在PEAKS中，关键词使用一个公钥进行加密，没有对应私钥的用户需要从授权机构获得授权才能搜索关键词。每次授权过程由授权机构向用户签发一个随时间更新的授权令牌来完成。获得授权的用户随后可以搜索被授权的关键词。其次，我们构建了一个可证明安全的PEAKS方案，该方案允许授权机构授权用户搜索不同的关键词集。授权过程的特点是授权令牌的大小为常数，与被授权关键词集的大小无关。用户可以为其被授权关键词集中的关键词生成陷门。测试过程的成功取决于：陷门新鲜性、陷门授权性和关键词一致性。我们形式化地证明了该方案在选择关键词攻击下的语义安全性和陷门不可伪造性。

1.1 相关工作

宋等人[22]率先开展了对称可搜索加密（SSE）的研究，但该技术无法实现与其他实体之间的加密数据共享。在共享数据时，SSE需要向用户分发私钥，导致复杂的密钥分发/管理问题。SSE在性能方面有许多改进[9,10,16]。

博恩等人[5]提出了PEKS的概念以解决上述弱点，并给出了一个具体方案。在他们的方案中，发送方使用关键词和用户的公钥创建可搜索的密文。用户使用其私钥和关键词生成陷门，并将陷门提供给服务器进行搜索。只有当陷门中的关键词与密文中的关键词匹配时，服务器才会将相应的加密数据返回给用户。

自PEKS提出以来，许多PEKS变体被提出以改进PEKS。支持合取关键词搜索的公钥加密（PECKS）方案[2,3,7,17–19]被提出以增强查询表达能力。在[2,17,18]中实现了基于PECKS的可组合多关键词搜索。Bethencourt等人[3]提出了支持合取关键词范围搜索的公钥加密方案。Boneh和Waters[7]应用了一种称为隐向量加密（HVE）的新技术，以实现合取、范围和子集关键词搜索。Sedghi等人[19]利用通配符来提高搜索查询的可扩展性和表达能力。具有扩展关键词的PEKS方案[1,8]被提出以增强数据库系统的可用性。Abdalla等人[1]基于从匿名身份基加密（AIBE）到PEKS的通用转换，构建了带临时关键词搜索的公钥加密（PETKS）方案以保证一致性。Camenisch等人[8]提出了无感知关键词搜索的公钥加密（PEOKS），并基于PEOKS构造了一个授权的私人信息检索（PIR）方案。然而，PEOKS采用了计算成本较高的承诺和零知识证明（ZKP），且他们提出的方案要求用户下载整个数据库，这既低效又不实用。基于属性的加密（ABE）的数据搜索方案[21,23,25]被提出以利于数据搜索控制。Sun等人[23]设计了支持用户撤销的属性基关键词搜索方案，适用于多用户和多贡献者场景。Zheng等人[25]构造了可验证的基于属性的关键词搜索（VABKS）方案，以解决服务器忠实搜索的验证问题。Shi等人[21]也提出了一种基于ABE的可搜索加密，以支持细粒度搜索和访问控制。这些方案关注用户身份/属性控制而非关键词控制，若直接用关键词替换属性，则关键词隐私将受到损害。带关键词搜索的代理重加密（PRES）[12,20,24]被提出，允许代理服务器执行测试函数和委托解密，该方案结合了代理重加密（PRE）和PEKS两种原语。然而，这些PRES方案未考虑基于关键词的授权。

短密钥的生成已在一些公钥加密方案[6,11,13–15]中进行了研究。由于关键词隐私和陷门生成的原因，这些方法不能直接应用于搜索的授权密钥。因此，如何实现固定大小的授权令牌并减少授权过程中的带宽消耗是一个具有挑战性的问题。

组织结构

本文其余部分的组织结构如下：在第2节中，我们描述了授权关键词搜索系统及相关定义。第3节给出了具有固定大小授权密钥的PEAKS构造，并在第4节中对其安全性进行了形式化证明。最后，我们在第5节中对全文进行总结。

2 问题描述

2.1 系统模型

一个PEAKS系统包含发送方、服务器、授权机构和用户，如图1所示。该系统中仅有一个公钥/私钥对（pk, sk），且 pk被公开。

• 发送方 。它将加密数据和加密关键词上传至服务器进行存储和索引，其中存储的数据可能对所有系统用户可用。
• 授权机构 。它在系统中充当管理者角色，并保管 sk的机密信息。它通过签发新的授权令牌，在新的时间点对在线用户重新进行授权。
• 用户 。它为某些授权关键词生成陷门，并将其提交至服务器以进行搜索，其中只有授权用户才能生成有效陷门。
• 服务器 。它执行授权验证和关键词匹配操作，并决定是否向用户返回相应数据。它是诚实但好奇的，诚实地执行搜索操作，但会好奇地从加密关键词中推断关键词。

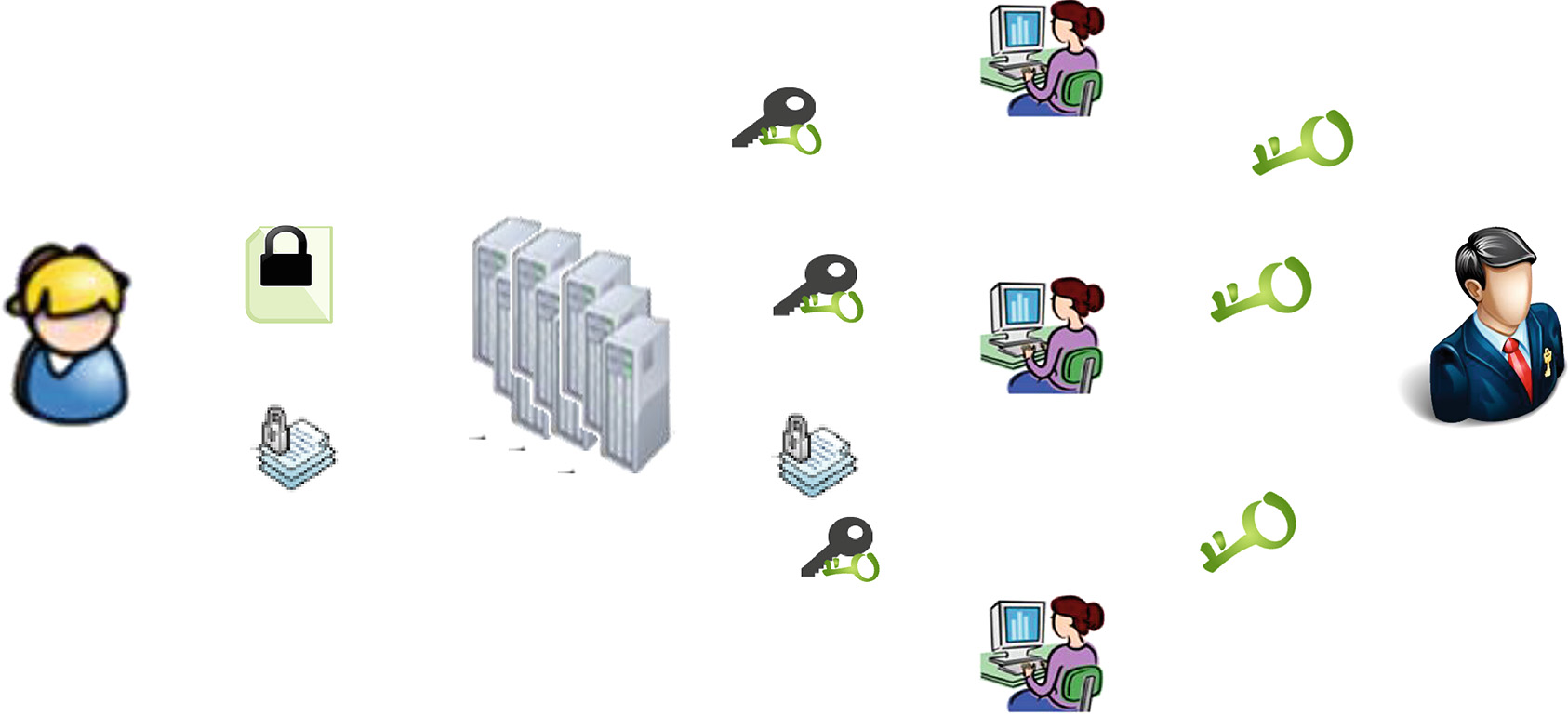
工作流程 。PEAKS系统通常为注册用户提供数据索引服务，且不考虑用户之间的共谋行为。发送方上传的数据包括用于共享的加密数据和用于索引的加密关键词PEKS。发送方使用 pk和特定关键词 w生成可搜索密文 PEKS。用户需要获得授权机构的授权才能拥有搜索权限。授权机构向不同用户授权不同的关键词集，其中某些在线用户 Useri被授予关键词集Wi。对于授权时间 t，授权机构生成授权令牌 tokeni。

2.2 算法定义

定义 1 . PEAKS方案由以下算法组成。

• 设置 (1^k)。输入安全参数 1^k，输出系统公钥和私钥(pk, sk)。
• 授权 （Authorize）(sk, W, t)。输入为私钥 sk、授权关键词集 W 和授权时间 t，输出为授权密钥 ak 及其签名 σ。然后，授权令牌表示为 token=(ak, σ, t)。
• 加密 (pk, wi)。以公钥 pk和关键词 wi作为输入，输出可搜索密文 PEKS。
• 陷门 (pk, token, w′i)。输入公钥 pk、授权令牌token和关键词 w′i ∈ W，输出一个陷门 T。然后，陷门元组表示为 TT=(T, σ, t)。
• 测试 (pk, P EKS, T T, t′)。输入公钥 pk、可搜索密文 PEKS、陷门元组 T T和陷门接收时间 t′，如果 t′ ≤ t、σ可以被接受且 wi= w′i，则输出1；否则输出0。

正确性 。带授权关键词搜索的公钥加密的正确性必须满足：对于系统参数 (pk, sk)、令牌 token ←Authorize(sk, W, t)、密文 PEKS ← Encrypt(pk, wi)、陷门 TT ←Trapdoor(pk, token, w′i)以及陷门接收时间 t′，如果 t′ ≤ t，则 TT中的签名可被验证且 wi= w′i，我们能够得到Test(pk, P EKS, T T, t′) = 1。

2.3 安全性模型

我们分别从针对选择关键词攻击的语义安全（SS‐CKA）和陷门存在不可伪造性（T‐EUF）两个方面定义了两个游戏。假设通用关键词空间为 U。

针对选择关键词攻击的语义安全

SS‐CKA游戏遵循博恩等人提出的模型[5]并允许攻击者 A发起选择关键词攻击。A获得一些私钥和陷门，但需满足一定限制，并试图区分关键词 w0的可搜索密文与关键词 w1的密文，其中他无法获得相应的陷门。A与挑战者 C进行如下交互。

• 初始化 。攻击者 A声明挑战关键词集 W∗ ⊆ U。
• 设置 。C运行设置算法并将公钥 pk发送给 A。
• 阶段1 。A执行多项式有界数量的查询。
• 授权查询 。A向 C提交关键词集 W= U − W∗和授权时间 t以进行授权查询。C通过运行授权算法，将授权令牌token返回给 A。
• 陷门查询 。A向 C提交关键词wi和时间 t。C通过运行陷门算法，将陷门元组 T T返回给 A。
• 挑战 。A生成两个等长的关键词 w0，w1 ∈ W∗，并希望就此接受挑战。A此前未查询过W∗的授权令牌，或 w0，w1的陷门。C随机选取一个比特 b ∈{0, 1}，并向 A返回挑战密文 PEKS∗b。
• 阶段2 。A继续请求对任意关键词的授权查询和陷门查询，直至wi ≠ w0, w1。C按照阶段1的方式进行响应。
• Guess 。A输出一个比特b′ ∈{0, 1}，如果 b′= b，则赢得游戏。

定义2 。如果不存在能够以不可忽略的优势 ε 赢得上述游戏的概率多项式时间 (PPT) 对手 A，则 PEAKS 方案可提供针对选择关键词攻击的语义安全。

陷门存在不可伪造性

该T‐EUF游戏允许攻击者 A发起冒充攻击。显然，如果攻击者已被授权，则很难防止冒充攻击。A被允许在某些限制下查询授权和陷门，且 A试图伪造一个有效陷门。A与挑战者进行如下交互。

• 初始化 。攻击者 A声明挑战关键词集 W∗。
• 设置 。挑战者 C运行设置算法，并将公钥 pk发送给 A。
• Query 。A执行多项式有界数量的查询。
• 授权查询 。A向 C提交关键词集和授权时间 t，C通过运行授权算法向 A返回授权令牌 token。
• 陷门查询 。A向 C提交关键词wi和 t，C通过运行陷门算法向 A返回陷门元组 T T。
• Forgery 。A输出一个未被查询过的关键词集W∗的陷门元组。

定义 3 。如果不存在能够以不可忽略的优势 ε 伪造出具有正确签名和时间的有效陷门的 PPT 攻击者 A，则 PEAKS 方案提供陷门不可伪造性。

2.4 困难问题

我们提出了两个多序列指数Diffie‐Hellman（MSE‐DH）问题，它们是[4]中一般Diffie‐Hellman指数问题的两个特例。不可解性分析见完整版本。

(n, l)‐MSE‐DDH 问题 。设 n 为整数，且(p, G, GT, e(·,·)) 为一个双线性映射群系统。设 g0, h0 为 G 的生成元。给定在 α 中具有两两不同根的随机互素多项式 q1, q2, q ，其对应的次数分别为 deg q1= l − 1, deg q2= n − l 和 deg q= 1，以及若干群元素序列，

S1=
⎧ ⎪⎪⎪⎨ ⎪⎪⎪⎩
g0, ···, gα n−1 0 , gβ1 0, gβ2 0, grβ1 0, g0x, hβ1β2q2 0 , hsβ1β2q1q 0 , hβ1q1q2q 0 , ···, hβ1α n−1q1q2q 0 ,
hβ2q1q2q 0 , ···, hβ2α n−1q1q2q 0 , hsβ1q1q2q2 0 , ···, hsβ1αl−2q1q2q2 0 ,
hsβ2q1q2q2 0 , ···, hsβ2αl−2q1q2q2 0 ,

并且 Z ∈ G，区分 Z是否等于 grq1q2 0 或是 G的一个随机元素。

(n, l)‐MSE‐CDH 问题 。设 n为整数，g0为群G的生成元。给定在 α中具有两两不同根的随机互素多项式 q1, q2，其对应的次数分别为 deg q1= l, deg q2= n − l，以及若干群元素序列，

S2=
⎧ ⎪⎨ ⎪⎩ g0, ···, gα n−1 0 , gβ1 0, gβ2 , hβ1β2q2 0 , g0a, gb 0, gc 0, gab 0, gbc 0, gac 0,
hβ1q1q2 0 , ···, hβ1α n−1q1q2 0 , hβ2q1q2 0 , ···, hβ2α n−1q1q2 0 ,

其中 a, b, c ∈ Zp，计算 gabc 0 ∈ G。

3 带授权关键词搜索的公钥加密

在本节中，我们给出了一个具体的PEAKS方案及其效率分析。借助互补集的性质，我们在PEAKS构造中的令牌实现了常数大小，且不依赖于授权关键词集的大小。由于我们关注的是协商关键词的授权，用户撤销不在我们的研究范围内，授权机构生成的令牌将仅随时间颁发给用户。

3.1 双线性配对

设 G, GT是相同素数 p的两个循环群，且映射 e: G× G → GT是一个双线性配对[5]。

• 双线性 ：对所有 g, h ∈ G 和 a, b ∈ Zp ，有 e(g a, hb) = e(g, h)ab。
• 非退化 ：若 g ∈ G, e(g, g) 是 GT 的生成元。
• 可计算性 ：存在一个高效算法用于计算 e(g, h)，其中 g, h ∈ G。

3.2 构造

设置 (1^k)。系统在安全性级别 k下生成双线性配对群(p, G, GT, e)。选择群G的生成元 g, h ∈ G以及秘密值 α, x, β1, β2 ∈R Zp，并设定 u1= gβ1, u2= gβ2, v1= hβ1, v2= hβ2 。选取两个密码学单向哈希函数 H1: {0, 1}∗ → Zp和 H2: {0, 1}∗ → G。通用关键词空间表示为 U，其大小为 n。公钥/私钥由授权机构公开/保存

pk=(g, gα,···, gα n−1, gx,{ui, vi, v α }i=1,2), sk=(α, x, β1, β2, h).

授权 (sk, W, t)。对于某个在线用户，我们假设授权机构会将关键词集 W(W ⊆ U)授权给该用户，其中 W的大小为 l, l ≤ n。为了提高可读性，首先设置多项式

f1(α)= ∏ wj∈U (α+ H1(wj)),
f2(α)= ∏ wj∈W (α+ H1(wj)),
F(α)= f1(α) f2(α) = ∏ w j∈U −W (α+ H1(wj)).

进行时间更新时，授权机构将使用新的授权令牌重新授权用户。授权机构选择 s ∈R Zp，并结合其签名生成授权密钥

ak= hβ1β2 F(α), σ= H2(aks, t) x,

其中 t是授权时间。通过安全通道向用户分发授权令牌 token=(ak, σ, s, t)。

加密 (pk,wi)。发送方选择 r, r1 ∈R Z p并计算

PEKS=(C1= g rf1i( α), C2= ur−r1 1 , C3= ur1 2)

作为可搜索密文，其中 f1i(α)= f1 (α)α+H1(wi)对于 wi ∈ U, gf1i (α)可以从 g, g α,···, g α n − 1 计算得到。然后将其上传至服务器。

陷门 (pk, token, wi)。授权用户使用接收到的授权元组计算陷门

T=(T1= ak s , T2= v s f2i( α) 1 , T3= v s f2i( α) 2 ),

其中 f2i(α) = f2(α) α+H1(wi) 对于 wi ∈ W 且 vf2i(α) 1 ， vf2i(α) 2 可从 v1, v1α,···, vαn−1 , v2, v2α,···, vαn−1 计算得到。然后将陷门元组 TT=(T, σ, t) 发送给服务器进行搜索。

测试 (pk, P EKS, T T, t′)。当服务器在时间 t′ 收到元组 (T, σ, t) 时，首先检查 t′ ≤ t 是否成立。若成立，则陷门处于授权时间内。服务器通过验证签名为真来确认

e(σ, g)=? e(H2(T1, t), gx).

如果等式成立，则该陷门来自授权用户。然后服务器进行检查

e(C1, T1) =? e(C2, T3)· e(C3, T2).

如果等式成立，则输出1，服务器将相应的加密数据返回给授权用户，否则输出0。

正确性 。我们证明了我们的构造满足第2.2节中所声称的正确性要求。2.2。

如果陷门中的签名是由授权机构正确签发的，则可以通过以下方式验证：

e(σ, g)= e(H2(aks, t)x, g)= e(H2(aks, t), gx)= e(H2(T1, t), gx).

那么，如果可搜索密文 PEKS和陷门 T中的关键词相同，即wi，我们有

e(C1, T1)= e ⎛ ⎝g r ∏ w j ∈U,j≠i (α+H1(wj)) , h sβ1β2 ∏ w j ∈U−W (α+H1(wj)) ⎞ ⎠
= e(g, h) rsβ1β2 ∏ w j ∈W ,j≠i (α+H1(wj))
= e(ur−r1 , v s ∏ w j ∈ W, j≠ i (α+H1(wj)) 2 )· e(ur1 2, v s ∏ w j ∈ W, j≠ i (α+H1(wj)) 1 ) = e(C2, T3)· e(C3, T2).

3.3 效率

我们分析了不同阶段的通信开销，其中 |G|, |GT|, |t| 分别表示群 G, GT和时间戳 t中一个群元素的大小。发送方运行加密算法上传数据。可搜索密文的大小代表了发送方与服务器之间的通信开销。它在群 G中占用3个群元素。当进行时间更新时，授权机构需要通过新的授权令牌对在线用户重新授权。在每次授权过程中，授权机构为关键词集 W签发一个固定大小的授权令牌。授权阶段的带宽消耗主要由授权令牌 token的大小决定，其开销为 G中的2个群元素和一个时间戳，与授权关键词集 W的大小无关。为了检索数据，用户需要运行陷门算法并向服务器提交陷门元组。带宽消耗主要取决于陷门元组 TT 的大小，在群 G 中占 4 个群元素和一个时间戳。

计算开销也在相应的阶段中给出，其中exp、 mul、 h分别表示执行模幂运算、模乘运算和哈希函数所需的时间。在加密阶段，发送方需要(n+ 2)exp+(n−1)mul来生成密文。在授权阶段通过时间更新，授权机构为用户计算一个令牌，耗时为3exp+ 1h，且与关键词集 W的大小无关。用户在陷门阶段需要支付 (2n+1)exp+(2n−2)mul来为某个关键词生成陷门。分析结果列于表1。由于令牌随时间频繁更新，因此在我们的PEAKS中，授权阶段的计算开销和通信开销应被优先考虑。通过上述分析可知，PEAKS能够实现快速的令牌生成以及授权机构与用户之间恒定大小带宽。较短的令牌是以增加 O(n)生成密文和陷门的开销为代价的，这是本PEAKS方案中的一种权衡，将在未来的工作中进一步研究。

阶段	通信开销	计算开销
加密	3|G|	(n+1)exp+(n − 1)mul
授权	2|G| + |t|	3exp+1h
陷门	4|G| + |t|	(2n+1)exp+(2n − 2)mul

表1. 通信开销。

4 安全证明

4.1 SS‐CKA

定理1 。如果在概率多项式时间内难以解决（n, l）‐MSE‐DDH问题，则所提出的PEAKS方案在随机预言机模型下对选择关键词攻击是语义安全的。

证明 。假设在SS‐CKA游戏中存在一个概率多项式时间对手 A，能够以优势 ε攻击我们的方案，那么我们可以构建一个针对(n, l)-MSE-DDH问题的优势为ε/eqT的模拟器 B 。 B的运行时间与 A大致相同。假设通用关键词空间为 U，其大小为 n。

• 初始化 。攻击者 A声明挑战关键词集 W∗，其大小为 l。

• 设置 。模拟器 B接收到一个群系统(p, G, GT , e(·,·))作为输入，以及一个(n, l)-MSE-DDH实例 S1。我们还有互素多项式 q1 , q2 , q，其阶数分别为 l − 1, n − l, 1，且它们具有两两不同的根。 B还被给予 Z ∈ G，其中 Z要么等于 g r q 1 q 2 0 ，要么等于某个随机元素 G的。我们将挑战关键词集记为 W ∗={w1,···, wl}。 B指定一个关键词 wθ ∈ W ∗。它隐式地设置了多项式
  q1(α)= ∏ l i=1,i≠θ (α+ ai), q2(α)= ∏ n i=l+1 (α+ ai), q(α)= α+ aθ.
  对于 i ∈[1, l], i ≠ θ，我们设 q1i(α)= q1(α) α+ ai。模拟器 B正式设置g= g0, h= hq1q2q 0 ，并且我们有
  u1= gβ1 0, u2= gβ2 0, gx= g0x,
  v1= hβ1q1q2q 0 , ···, vαn−1 1 = hβ1α n−1q1q2q 0 ,
  v2= hβ2q1q2q 0 , ···, vαn−1 2 = hβ2α n−1q1q2q 0 .
  B发送 A公钥
  pk=(g0,···, gα n−1 , g0x,{ui, vi,···, vα n−1 }i=1,2).

• H1查询 。 B维护哈希列表 L(wi, hi)，该列表初始为空。当收到对 wi的 H1查询时，如果 wi在列表 L中，则 B将对应的hi返回给 A。否则， B按如下方式设置哈希值 hi。
  hi= H1(wi)={aθ, if wi= wθ, ai, if wi ≠ wθ.
  然后 B将(wi, hi)添加到列表中，并将 hi返回给 A。

• H2查询 。 B维护一个哈希列表 L′(aksi, ti, ri, h ′ i)，该列表初始为空。当收到对( aksi, ti)的 L′查询时，如果其在列表 L′中，则 B返回相应的 h′ i给 A。否则， B选择 ri ∈R Zp并设置哈希值h′ i= H2(aksi, ti) = g ri ′ i) 添加到列表中，并将 hi返回给 A。

• 阶段1 。

• 授权查询 。 A针对时间 ti的关键词集U − W∗查询授权令牌。对于每个关键词 wi ∈ U − W∗，设(wi, hi)为 L列表上的相应元组，且我们有 hi= H1(wi) = ai，其中i ∈[l+ 1, n]。 B获得ak= h β1β2q2 0 ，其中
  ak= h β 1 β 2 ∏ w j ∈ U −( U − W ∗ ) ( α+H1( w j )) = h β 1 β 2 q1 q2 q q1 q 0 = h β1β2q2 0 .
  B选择 si ∈R Z p ，设(aks i, ti, ri, h ′ i)为列表 L′上对应的元组，我们有 h′ i = H2( aks i, ti) = g r i 0，且签名为 σ= g xr i

• 陷门查询 。当 A针对关键词 wi 在时间 ti 发起陷门查询时， B执行陷门算法并向 A返回模拟结果。
  如果 wi ∈ U − W ∗， A可以使用上述授权查询获取授权令牌，并自行生成陷门。
  •如果 wi ∈ W∗， B将响应以下陷门。
  * 如果 wi= wθ，则输出中止。
  * 如果 wi ≠ wθ，令 (wi, hi) 为 L 列表上对应的元组，且我们有 hi= H(wi) = ai，其中 i ∈[1, l], i ≠ θ。 B 选择 s′′ ∈R Z∗ p 并计算陷门 T 作为
  T1=(hsβ1β2q1q 0 )s′′ , T2=(hsβ1q1q2q2q1i 0 )s′′ , T3=(hsβ2q1q2q2q1i 0 )s′′ ,
  其中 T1 直接来自 hsβ1β2q1q 0 和 T2, T3 可以从 (n, l)-MSE-DDH 问题 实例中的元素 hsβ1q1q2q 2 0 ,···, hsβ1α l−2q1q2q 2 0 、 hsβ2q1q2q 2 0 ,···, hsβ2α l−2q1q2q 2 0 计算得出。
  可以通过隐式设置 s′= s′′s来验证陷门，然后
  T1= aks′=(h β1β2 q1 q2 q q2 0 )s′ =(hsβ1β2q1q 0 )s′′ ,
  T2= v s′ ∏ w j ∈W,j≠i (α+H1(wj)) 1 =(hβ1q1q2q 0 )s′q1iq=(hsβ1q1q2q 2 q1i 0 )s′′ ,
  T3= v s′ ∏ w j ∈W,j≠i (α+H1(wj)) 2 =(hβ2q1q2q 0 )s′ q1iq=(hsβ2q1q2q 2 q1i 0 )s′′ .
  设(aks′ , ti, ri, h ′ i)为列表 L′上对应的元组，我们有h′ i= H2(T1, ti) = g ri 0。
  签名被隐式设置为 σ= g xri 0 。 B向 A返回响应 T T=(T, σ, ti)。

• 挑战 。 A生成一对它希望被挑战的关键词 w0, w1 ∈ W ∗，并将(w0, w1)发送给 B。 A之前未查询过 W∗的授权令牌，或 w0, w1的陷门。 B按如下方式响应。

• 如果 wθ∈/{w0, w1}, B输出失败并终止。

• 否则，我们得到 wθ ∈{w0, w1}。令(wθ, hθ)为 L列表上对应的元组，并且我们有hθ= H1(wθ) = aθ。 B选择 r1 ∈R Z p，并以挑战密文响应A
  PEKS ∗=(C1= Z, C2= g rβ1 0 u −r1 1 , C3= ur1 2).
  这些项可以从(n, l)-MSE-DDH实例的元素中获得。注意，如果Z= g rq 1 q 2 0 ，通过 设置 r′= r，可以验证
  C1= g r ′ ∏ w j ∈ U , j ≠θ (α+H1(w j )) = g rq1q2 0 = Z,
  C2= u r ′ −r 1 1 = g β 1(r−r 1) 0 = g rβ 1 0 u −r 1 1 , C3= u r 1 2 .

• 阶段2 。 A继续请求对任意关键词的授权查询和陷门查询，直到 wi ≠ w0, w1。 C按照阶段1的方式响应。

• Guess 。 A输出其猜测θ′，若满足 θ′= θ则赢得游戏。

这完成了我们模拟的描述。如果 B不中止，则| Pr[θ′= θ] − 1 2| ≥ ε。该概率取决于 A和 B所使用的随机比特，如下所示，其中 B的运行时间与 A的大致相同。根据上述过程，在阶段1或阶段2中，陷门查询导致 B中止的概率为 1/ (qT+ 1)，而授权查询不会导致 B中止。假设 A总共进行了 qA次授权查询和 qT次陷门查询，则所有查询均未导致 B中止的概率至少为(1 − 1/(qT+ 1)) qT ≥ 1/e。在挑战阶段，如果 A能够生成 w0、 w1且满足 wθ∈/{w0, w1}，则 B将中止。因此，Pr[wθ= wi]= 1/(qT+ 1)对于 i= 0和1成立，并且这两个值彼此独立，我们有Pr[wθ ≠ w0, w1]=(1 − 1/(qT+ 1))2 ≥ 1 − 1/qT。因此， B不中止的概率至少为 1/qT。注意到由于 A永远无法对挑战关键词w0、 w1进行查询，因此 B的优势至少为 ε/eqT。

4.2 T‐EUF

定理2 。如果在多项式时间内（n, l）‐MSE‐CDH问题是困难的，那么PEAKS方案在随机预言模型中具有陷门存在不可伪造性。

证明 。假设在T‐EUF游戏中存在一个概率多项式时间对手 A，能够以优势 ε攻击我们的方案，我们构造一个模拟器 B，其针对(n, l)-MSE-CDH问题的优势为 ε/ ((1+qA)e)。 B的运行时间与 A大致相同。假设通用关键词空间为 U，大小为 n。

• 初始化 。攻击者 A 声明挑战关键词集 W∗，其大小为 l。

• 设置 。模拟器 B获得(n, l)-MSE-CDH实例S2。我们还有互素多项式 q1, q2，其阶数分别为 l, n − l，且它们的根两两不同。 B的目标是输出 g abc 0 ∈ G。我们记为 W∗={w1,···, wl}。它设置
  q1(α)= ∏ l i=1 (α+ ai), q2(α)= ∏ n i=l+1 (α+ ai).
  模拟器 B隐式设置 g= g0, h= hq1q2 0和 x= a，我们有
  u1= g β1 0 , u2= g β2 0 , g x= g a 0 , v1= h β 1q1q2 0 , ···, vα n − 1 1 = h β 1 α n − 1 q1q2 0 , v2= h β 2q1q2 0 , ···, vα n − 1 2 = h β 2 α n − 1 q1q2 0 .
  然后 B发送 A公钥
  pk=(g0,···, g α n − 1 0 , g a 0 ,{ui, vi,···, v α n − 1 i }i=1,2).

• H1查询 。 B维护哈希列表 L(wi, hi)，该列表初始为空。当收到对 wi的查询时，如果 wi在列表 L中，则 B将对应的 hi返回给 A。否则， B选择 ai ∈ Zp并设置 hi= H1(wi)= ai。然后 B将(wi, hi)添加到列表 L中，并将 hi返回给 A。

• H2查询 。 B维护两个列表 L1 和 L2。

• B维护一个列表 L1(akWs1i∗, t1i, c1i, r1i, h1i)，该列表初始为空。当收到对(akWs1i∗, t1i)的查询时， B查找 L1以找到 h1i并将其返回给 A。如果(akWs1i∗, t1i)不在列表中， B检查 akWs1i∗是否在列表中。若不在， B创建一个元组(akWs1i∗, t1i, c 1 i, r 1 i, h 1 i)，其中随机选择 c1i, r 1 i ∈RZp并计算哈希值
  h1i= H2(aks1i W∗, t1i)={g r1i 0 gc 0, if c1i= t1i, r1i 0 gbc 0, if c1i ≠ t1i.
  然后 B将(aks1i W∗, t1i, c 1 i, r 1 i, h 1 i)添加到 L1中，并将相应的 h1i返回给 A。如果是，则表示 aks1i W∗之前已被询问过，也就是说 A曾针对不同的 t1i发起过哈希查询。 B查找列表以获取 c1i，随机选择另一个 r1i，根据上述函数计算相应的哈希值，将结果添加到列表中，并将结果发送给 A。

• B维护一个列表 L2(aks i U−W∗, t2i, c2i, r2i, h2i)，该列表初始为空。当收到对( aks2 i 不在列表中， B将检查 aks2 i U−W∗是否在列表中。 2 如果否， B随机选择c2i, r 2 i ∈R Z p并计算以下哈希值，生成一个元组(ak s 2 i 2 i, r2i, h 2 i) 2 h2i= H2(ak s 2 i U−W ∗ , t2i)={g r 2 i 0, if c2i= t2i, r 2 i 0 g b 0, if c2i ≠ t2i. B将(ak s 2 i U−W ∗ , t2i, c2i, r2i, h2i)添加到列表 L2中，并向 A返回相应的 h2i。如果是，则表明 ak s i U−W ∗ 之前已被询问过，也就是说 A针对不同的 t2i发起 了哈希查询。 B查找列表以获取 c2 i，随机选择另一个 r2 i，根据上述函数计 算相应的哈希值。然后 B将该元组添加到列表中，并将结果发送给 A。

• 查询 。

• 授权查询 。 A可以按如下方式请求授权令牌。
  如果关键词集为 W ∗，对于每个关键词 wi ∈ W ∗，设(wi , hi)为在 L列表上对应的元组，且我们有 h i= H 1( w i)= a i，其中 i ∈[1, l]。 B计算ak= h β 1 β 2 q 1 0 。然 后 B选择 s 1 i ∈ Z p 并查找列表 L 1以找到对应的 c 1 i 。如果 t 1 i ≠ c 1 i ，输出中止。
  否则， B设置 t1i= c1i并从 L1获取 r1i。 B计算 σ= gac 0 gar 1 i 0并响应 token=(ak, σ, s1i, t1i)给 A。可以验证其有效性
  ak= h β1β2 ∏ wj∈U−W ∗(α+H1(wj))= h β1β2 q1 q2 q2 0 = hβ1β2q1 0 ,
  σ= H2(aks1i, t1i) x=(gc 0g r1i 0)a= gac 0 gar 1 i 0.
  如果关键词集为U − W ∗，对于每个关键词 wi ∈ U − W ∗，设(wi, hi)为 L列表上对应的元组，且我们有 hi= H1(wi) = ai，其中 i ∈[l+ 1, n]。 B计算ak= hβ1β2q2 0 。可通过以下方式验证
  ak= h β1β2 ∏ wj∈U−(U−W∗) (α+H1(wj))= h β1β2 q1 q2 q1 0 = hβ1β2q2 0 .
  然后 B选择 s2i ∈ Zp 并查找列表 L2 以找到对应的 c2i。* 如果 t2i= c2i，则从 L2 获取 r2i。 B 响应 token=(ak, σ, s2i, t2i) 到 A, where σ= H2(aks2i, t2i) x =(g r2i 0)a = g ar2i 0. * 如果 t2 ≠ c2，从 L2 获取 r2， B 返回 token=(ak, σ, s2i, t2i) 给 i i i A, where σ= H2(aks2i, t2i) x =(gb 0g r2i 0)a = gab 0 g ar2i 0.

• 陷门查询 。 A可以请求关键词wi的陷门。 A可通过授权查询获得授权令牌 token，并自行生成陷门。

• 伪造 。 A输出一个陷门 TT=(T∗, σ∗, t1∗)，用于wi ∈ W ∗在时间 t1∗的查询，其中 T∗=(T∗ 1, T∗ 2, T∗ 3)和(T∗ 1, t1∗)此前未被查询过。由于 T T=(T∗, σ∗, t1∗)是一个有效陷门元组，σ∗是一个有效签名，且它隐含地表示(aks1 ∗ W∗, t1∗, c1∗, r1∗, h1∗)在列表 L1上。

• 如果 t∗= c1∗，输出中止。
• 如果 t∗ ≠ c1∗，输出 σ ∗ g ar 1∗ 0 作为(n, l)-MSE-CDH 问题的解。由于 H2(aks 1 ∗ bc 0 g r 1 ∗ 0, σ∗= H2(T∗ 1, t1∗) x= H2(aks 1 ∗ W∗ , t1∗) x =(g bc 0 g r 1 ∗ 0) a = g abc 0 g ar 1 ∗ 0 , 我们可以通过 g abc 0= σ ∗ g ar 1 ∗ 0 提取g abc 0 。

这完成了我们模拟的描述。根据定理1中的方法，且我们有 B的优势为 ε/((1+ qA)e)。

5 结论

我们提出了一种新的带授权关键词搜索的公钥加密概念，该概念扩展了PEKS原语。在PEAKS中，关键词被使用一个公钥加密，每个授权用户无需私钥即可从授权机构获得搜索权限。授权机构将带有时间的授权令牌分发给用户，用户可为任意授权关键词生成陷门。我们构建了一个可证明安全的PEAKS方案，其中授权令牌的大小与关键词集的大小无关。该方案显著减少了授权机构与用户之间的带宽，并且仅允许使用正确关键词生成的最新授权陷门通过服务器的测试。我们证明了该方案在面对选择关键词攻击时具备语义安全性和陷门不可伪造性。