搞清楚p问题、NP问题、NP完全问题和NP难问题

先行了解相关的几个名词：

计算复杂性理论：

研究计算资源中最常见的时间（要通过多少步演算才能解决问题）和空间（在解决问题时需要多少存储器）

归约：

是解决不同算法问题的一种手段。比如有两个算法任务A and B，假如任务A比任务B的复杂性低（简记为A≤B）。从归约的角度来看，就是说如果我们有了B的有效算法M，那么我们有一个有效算法N，它可以引用M，最终解决A问题。
所以 A≤B 等价 A归约到B（reduces A to B, or A is reducible to B, or A can be reduced to B）。

时间复杂度

时间复杂度不是表示程序解决一个问题要花费的时间，而是表示 当问题规模（数据）增大后，程序处理需要的时间增长的有多快。比如当数据扩大n倍后，程序处理的时间变慢n倍，那就是O(n)的时间复杂度。再比如冒泡排序，数据扩大2倍，时间变慢4倍，就是O(n^2)的时间复杂度。

如下表所示，时间复杂度排序递减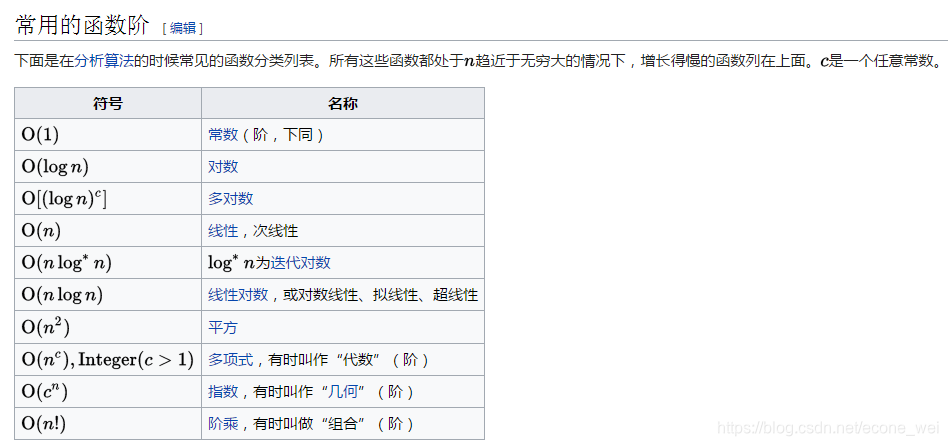

多项式时间

在计算复杂度理论中，指的是一个问题的计算时间 $m(n)$ 不大于问题 $n$ 的多项式倍数（即n为底数的时候）。数学描述为 $m(n)=O(n^k)$,此 $k$ 为一常量值。
如O(a^n)和O(n!)型的复杂度，属于非多项式级的复杂度，这种级别的复杂度计算机往往不能承受。

不可解问题

并非所有问题都可以找到多项式时间的算法，甚至有些问题不可能找到一个正确的算法。这样的问题就称为不可解问题。

Hamilton网络

在一个城市的地图网络中，寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径。

=========================================
辅助理解参考图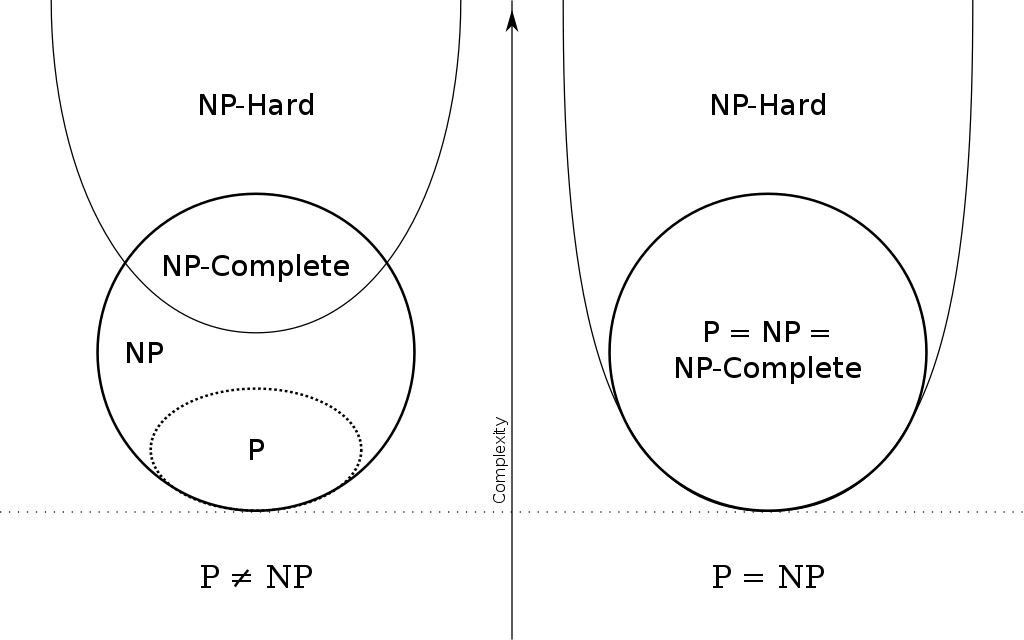

P类问题

能在多项式时间内解决的问题。（polynominal，多项式）

NP类问题

在多项式时间内验证(猜)一个正确解的问题。（Non-deterministic polynominal,非确定性多项式）

P类问题是NP问题的子集，因为存在多项式时间解的问题，总能在多项式时间内得到验证。
NP问题不一定能在多项式时间内得到验证，所以P问题并不等价于NP问题。

不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的额猜测过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。

Hamilton回路就是一个NP问题，比如要确定路径权值和小于某个参数W的解，那我随便猜一条，然后去验证，在多项式时间内总会解决这个问题。

NPC问题

存在一个NP问题 $Q$，如果所有NP问题都能在多项式时间内归约为这个 $Q$。也就是说只要解决了这个问题，那么所有的问题都解决了。（NPC：NP complete ,NP完全问题）
定义满足2个条件：

• 属于一个NP问题
• 所有NP问题都能归约到它

NPH问题

NP难(hard)问题是满足NPC问题的第二个条件，但不一定满足第一个条件，即NP-hard不一定是NP问题。也就是说NP-Hard问题可能无法得到多项式时间的算法。

.
.
.
.
参考资料：
http://www.matrix67.com/blog/archives/105

https://blog.youkuaiyun.com/databatman/article/details/49304295

https://zh.wikipedia.org/wiki/P/NP%E9%97%AE%E9%A2%98

https://blog.youkuaiyun.com/qq_29176963/article/details/82776543

（第一篇大佬讲的很详细，可参考）