文章目录
问题A:Necklace
题目:UVA11001
题意:
有一个部落的人用一些粘土制成直径相同的圆环,一个项链由多个原环组成,如图:
每个圆环的厚度是固定的。直径D和粘土体积V有一下关系:
其中V0表示消耗的体积
给出V,V0,V=V0=0结束
求出可以制作圆环的数量,使得形成的项链是最长的
**思路:**设被分成n份,那么长度x=n*0.3 V n − V 0 \sqrt{\frac{V}{n}-V0} nV−V0
考虑到根号,平方后求导化简可得,n= V 2 ∗ V 0 \frac{V}{2*V0} 2∗V0V 时为最大,这里考虑n的小数部分,=0.5多解输出0,<0.5向下取整,>0.5向上取整。//这里要考虑V=2V0的情况,输出1,
参考代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int V,v0;
while(cin >> V >> v0){
if(V==0 && v0==0) return 0;
double j = 1.0*V/(2*v0);
int x = V / (2*v0);
if(V <= v0){
cout << "0" << endl;
}
else if(V <= 2*v0){
cout << "1" << endl;
}
else if((j - x) == 0.5) {
cout << "0" << endl;
}
else if(j - x < 0.5) {
cout << x << endl;
}
else {
cout << x + 1 << endl;
}
}
return 0;
}
问题B:Bode Plot
题目:poj1045
题意:
给出电路图如图, V 1 = V s cos w t V_{1}=V_{s}\cos wt V1=Vscoswt
V 2 = V R cos ( w t + θ ) V_{2}=V_{R}\cos (wt+\theta) V2=VRcos(wt+θ) Vs是电源电压,w是角频率,t是时间, V R V_{R} VR是电阻R两端电压下降的幅度, θ \theta θ 是它的相位
ps:i = C d/dt (v1-v2)
输入 V s V_{s} Vs,R和C,n(表示测试样例),对于每一个测试样例,输入一个w表示频率w的值
求出 V R V_{R} VR的值,四舍五入保留三位小数
**思路:**物理题,推出公式,(可恶,居然把物理全还给老师了>=<
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include <vector>
#include<stack>
#include<map>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;
int main()
{
double Vs,R,C,w;
int n,i;
cin>>Vs>>R>>C>>n;
for(i=1;i<=n;i++)
{
cin>>w;
printf("%.3f",sqrt(1.0/(1+C*C*w*w*R*R))*C*w*R*Vs);
cout<<endl;
}
return 0;
}
问题C:Symmetric Matrix
题目:UVA11349
题意:
给出一个矩阵大小,输入矩阵,判断这个矩阵是不是对称的(水题~~
注意下输入输出的格式
参考代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll M[101][101] ;
int main()
{
int T,N;
char ch;
while (~scanf("%d",&T))
for (int t = 1 ; t <= T ; ++ t) {
getchar();
scanf("N = %d",&N);
for (int i = 0 ; i < N ; ++ i)
for (int j = 0 ; j < N ; ++ j)
scanf("%lld",&M[i][j]);
int flag = 1;
for (int i = 0 ; i < N ; ++ i) {
for (int j = 0 ; j < N ; ++ j)
if (M[i][j] < 0 || M[i][j] != M[N-1-i][N-1-j]) {
flag = 0;
break;
}
if (!flag) break;
}
printf("Test #%d: ",t);
if (flag)
printf("Symmetric.\n");
else printf("Non-symmetric.\n");
}
return 0;
}
问题D: Homogeneous Squares
题目:poj2941
题意:
给出一个n×n的方阵,对选定的元素求和,如果对于每一种选法,n个位置上的数的和相等,那就是输出"homogeneous" 否则输出"not “homogeneous”
思路:
对于n阶方阵,只需判断n-1阶方阵即可,递推可知,只需判断所有2×2的子方阵即可
注:需用scanf输出,cin输出会超时+=+
参考代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include <vector>
#include<stack>
#include<map>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;
int main()
{
int n;
while(scanf("%d",&n)!=EOF && n){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
scanf("%d",&mp[i][j]);
}
}
bool flag = true;
for(int i = 1; i < n; i++){
for(int j = 1; j < n; j++){
if(mp[i][j] + mp[i+1][j+1] != mp[i+1][j] + mp[i][j+1])
{
flag = false;
break;
}
}
}
if(flag) printf("homogeneous\n");
else printf("not homogeneous\n");
}
return 0;
}
问题E:Jill Rides Again
题意:
好家伙直接上wf的题目
题目:
Jill喜欢骑自行车,但自从她所居住的美丽的城市Greenhills大发展之后,Jill 就经常利用良好的公共汽车系统完成部分的旅行。她有一-辆折叠式自行车,在她乘公共汽车进行第一段的旅行时,她会随身携带。当公共汽车到达城市的某个令人愉快的地方时,Jill就下车骑自行车.她沿着公共汽车路线骑行,直刻到达目的地,或者她来到一个城市里她不喜欢的地方.在后–种情况下,她将登上公共汽车结束她的旅行.根据多年的经验,Jill 对每一条道路进行 了“良好性”的评分,分数为整数。正的“良好”值表示jill喜欢的道路:负值则表示她不喜欢的道路.吉尔要计划在哪里下公共汽车开始骑自行车,以及在哪里停下自行车并重新上公其汽车,使得她骑自行车经过的道路的良好值之和最大.这也意味着她有时会沿着-条她不喜欢的路骑自行车,前提是这条路连接了她的旅程的另外两个部分,她喜欢的道路能够足以补偿她不喜欢的道路.如果-.条路线的任何–部分都不适合骑自行车,则在整条路线上jill都会坐公共汽车:相反,如果一条路线都很好则Jill就根本不会坐公共汽车。。有许多不同的公共汽车路线,在每一条路线 上都有若千个车站,Jill 可以在那里下公共
有许多不同的公共汽车路线,在每一条路线 上都有若千个车站,Jill 可以在那里下公共汽车,或上公共汽车.她要求计算机程序帮助她确定每一条公共汽车路线上最适合骑车的部分
输入:
输入给出多条公交线路的信息。输入的第一行给出 一个 整数b,表示输入中路线的数.
每条路线的标识®是输入中的序列号,l<=r<=b.对于每条路线,首先给出路线上的站点数:一个整数s,2<=s<=20.000; 在站点数后面给出s-1行,第i行(1<=i<s)给出一一个整数m,表示Jill对第i站和第i+1站两个站点之间道路的良好性的评分。。
输出:对于输入中的每条路线r,您的程序给出起点公交车站i和终点公交车站j,它们给出良好值总和 m = n i + n i − 1 + ⋯ + n j − 1 m=n_{i}+n_{i-1}+\cdots +n_{j-1} m=ni+ni−1+⋯+nj−1最大的路线段.如果有多个路线段的良好值总和最大,则选择经过站点最多的路线段,即j-i的值最大.如果还有多个解,则选择i值小的路线段.对于输入中的每条路线r,按以下格式输出一行:
The nicest part of route r is between stops i andj
但是,如果良好值总和不是正数,则程序输出
Route r has no nice parts
解题思路:
题目是真的长,其实仔细一看就是求一个序列的子序列的最大值
算法如下:初始话ans=0;累加0到n-1个元素,每一步得到一个sum,如果sum>ans 则更新ans,如果sum<0,ans重置为0,最终ans就是最大的子序列和。此外,还需求出最大子序列的起点和终点,如果有多个解,需选择站点较多的解,具体细节看代码
参考代码:
#include<bits/stdc++.h>
using namespace std;
int a[20010];
int main()
{
int TC,r,cot=1;
scanf("%d",&TC);
while(TC--)
{
scanf("%d",&r);
int ans=0,sum=0,r1=1,r2=0,ans_r1=0,ans_r2=0;
for(int i=1; i<r; ++i) scanf("%d",&a[i]);
for(int i=1; i<r; ++i)
{
sum += a[i];r2 = i+1;
if(sum < 0) r1=i+1,sum=0;
else if( sum > ans || (sum == ans && r2-r1 > ans_r2 - ans_r1)) {
ans=sum;
ans_r2=r2;
ans_r1=r1;
}
if(ans > 0) printf("The nicest part of route %d is between stops %d and %d\n",cot++,ans_r1,ans_r2);
else printf("Route %d has no nice parts\n",cot++);
}
}
return 0;
}
问题F:To the Max
题目:poj1050
题目大意:
给出一个包含正负数的二维数组,一个子矩阵是指位于整个数组中大小为1*1或更大的任何子数组。矩阵和是该矩阵中所有元素的和
输入:一个整数n表示二维数组的大小,N最大值是100.数组中元素大小范围是[-127,127]
输出:最大子矩阵的和
思路1:
输入的时候进行列的前缀和处理,接下来采用降维处理,根据最大字段和求出答案,具体细节看代码
One:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include <vector>
#include<stack>
#include<map>
#include<string>
#include<cstring>
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
using namespace std;
typedef long long ll;
int a[105][105],sum[105][105];
int main()
{
IOS;
int n;
cin >> n;
int ans = -inf;
for(int i=1; i <= n; i++){
for(int j=1; j <= n; j++)
{
cin >> a[i][j];
sum[i][j] = sum[i-1][j] + a[i][j]; // 对每一列进行前缀和处理
ans = max (ans ,a[i][j]);
}
}
int now;
if(ans <= 0) cout << ans << endl;//都<0,输出最大的负数即可
else{
for(int i=1 ; i <= n; i++){ // 第一行,首行
for(int j=i ; j <= n; j++) //尾行
{
now = 0;
for(int k=1; k <= n; k++){ // 最大子段和
now += sum[j][k] - sum[i-1][k];
if(now < 0) now=0;
ans = max (ans, now);
}
}
}
cout << ans << endl;
}
return 0;
}
思路2;
先进行二维前缀和处理顶点到每个点的矩阵和,枚举求出最大子矩阵
ps:还好此题数据不大,O(n^4)不是大问题
参考代码:
#include <cstdio>
#include <sstream>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define inf 0x3f3f3f3f
using namespace std;
int mp[105][105];
int sum[105][105];
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
{
scanf("%d", &mp[i][j]);
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mp[i][j];
}
int ans = -inf;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
for(int k = i; k <= n; ++k)
for(int l = j; l <= n; ++l)
ans = max(ans, sum[k][l] - sum[i - 1][l] - sum[k][j - 1] + sum[i - 1][j - 1]);
printf("%d\n", ans);
return 0;
}

问题E:Who’s in the Middle
题目:poj2388
题意:
究极水题~~排序求中间的数,还确定了是奇数个,
sort大法好
代码:
#include<iostream>
#include<algorithm>
#include<cmath>
#define fn for(int i = 1; i <= n; i++)
using namespace std;
const int M =10010;
int cow[M];
int main()
{
int n;
cin >> n;
fn{ cin >> cow[i]; }
sort(cow+1, cow+1+n);
cout << cow[n/2+1] <<endl;
return 0;
}
问题H:Train Swapping
题目:UVA299
题意:
给定一列乱序的车厢,相邻的两节可调换,求最少要交换多少次才能把其调整为1…n的顺序。
思路: 选择排序,先把最小的调到第一个位置,第二小到第二位置…,最后得到的次数就是最优的。
参考代码:
#include<iostream>
using namespace std;
int main()
{
int rain[55];
int T,n;
cin>>T;
while(T--)
{
cin>>n;
int cnt=0;
for(int i=0;i<n;i++) cin>>rain[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<n;j++)
{
if(rain[j]==i)
{
for(int k=j;k>=i;k--)
{
int temp=rain[k];
rain[k]=rain[k-1];
rain[k-1]=temp;cnt++;
}
break;
}
}
}
cout<<"Optimal train swapping takes "<<cnt<<" swaps."<<endl;
}
return 0;
}
问题I:DNA Sorting
题目链接:poj1007
题意及思路:
输入m个长度为n的DNA序列,把他们按照逆序数从小到大稳定排序输出。
先求各个字符串的逆序数,再按逆序数对字符串快排,
参考代码:
#include<iostream>
#include<cstdio>
#include<cstring>
const int M = 200;
struct dna
{
char str[M];
int ans;
};
struct dna d[M];
struct dna t;
int main()
{
int n,m,i,j,k;
scanf("%d%d",&n,&m);
for(i=0;i<m;i++)
{
scanf("%s",d[i].str);
d[i].ans=0;
for(j=0;j<n;j++)
{
for(k=j;k<n;k++)
if(d[i].str[j]>d[i].str[k])
d[i].ans++;
}
}
for(i=0;i<m;i++)
for(j=i;j<m;j++)
{
if(d[i].ans>d[j].ans)
{
t=d[i];
d[i]=d[j];
d[j]=t;
}
}
for(i=0;i<m;i++)
{
printf("%s\n",d[i].str);
}
return 0;
}
总结:
- 前面几题还是数学,尤其那道物理>=<
- 后面的排序还是水题呀(就是最后哪题难搞QwQ)
- wf的题很好,读题两小时…





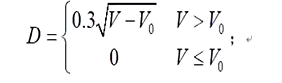


















 326
326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










