基于中颞区的生物启发运动计算模型

帕拉迪因：行为机器人杂志 2018年；第9卷：60–71页

研究论文 开放获取

费尔南达·达·C·E·C·法里亚*，乔治·巴蒂斯塔，和埃尔德·阿劳若

基于中颞区的生物启发式运动计算建模

https://doi.org/10.1515/pjbr‐2018‐0005 收稿日期： 2017年11月30日；接受日期：2018年3月3日

摘要 ： 本文描述了一种基于V1区（初级视皮层）和 MT细胞（中颞区）的仿生算法，用于运动计算。V1区 和中颞区神经元的行为包含理解运动感知的重要信息。
从计算的角度来看，神经元被视作二维滤波器，用以表示构成复杂细胞的简单细胞的感受野。本文提出一种改进的精细赖希哈特检测器，在最后阶段之前增加输出指数，并在分层框架中引入来自MT的调节性反馈的反馈阶段（V1区与中颞区的双向连接）。感受野周围具有抑制区域的端止型单元被建模为一种除法运算。MT细胞在整合和解释前一级（V1区）输入方面起着重要作用。我们采用归一化和池化操作来寻找最活跃的神经元以实现运动检测。所采用的所有步骤均受到生理机制启发，需要一定程度的简化和抽象。结果表明，与当前最先进的生物启发方法相比，本文提出的算法在真实世界图像上的性能更优。

关键词 ： 运动方向, 神经计算模型, 中颞区

1 引言

一种生物动机驱动的计算模型可以从神经生理学研究中得出。它们为我们提供了
*通讯作者：Fernanda da C. e C. Faria： 系统与机器人研究所，科英布拉大学，葡萄牙，电子邮箱： cunhaecastro@gmail.comJorge Batista： 系统与机器人研究所，科英布拉大学，葡萄牙，电子邮箱： batista@isr.uc.ptHelder Araújo： 系统与机器人研究所，科英布拉大学，葡萄牙，电子邮箱：helder@isr.uc.pt
对基本已知的功能性脑结构所遵循的原理进行理解，可以揭示这些概念与通用数学模型之间的关联信息，为开发受生物学启发的方法提供关键信息。

运动知觉的神经处理始于眼睛。观察场景至少有两个空间上分离的图像投射到二维视网膜表面。多个皮层区域参与对这些数据的解释。为了基于两个皮层区域研究这一现象，利用具有生理合理性的特征信息来整合视觉运动信号，以指导适当的算法模型模拟运动计算的逻辑。

为了理解生物神经运动检测系统如何组织以处理光流，我们提出了一种模型来估计图像序列的方向和速度。
我们描述的模型在空间上不限于经典感受野，而是考虑了感受野中心周围的区域。本研究采用改进的赖希哈特检测器（原始赖希哈特检测器加上时空滤波器）来研究神经运动信息感知。如我们之前的工作所述，V1细胞通过傅里叶域中的一组对数‐伽博滤波器建模[1]。我们探索了一种包含线性阶段（对数‐伽博滤波器）和乘法阶段的 V1细胞模型，其后还有一个额外的非线性输出（指数）。
随后，通过端止型单元计算V1中周围区域的抑制效应，这些单元是简单型和复杂型的亚型。之后，MT细胞通过计算除法归一化中的兴奋性和抑制性成分来实现来自 V1的输入的整合。我们将详细表征诱导方向选择性的机制、算法特性及其实现方式。

从计算视角出发，我们提出了将神经科学发现与视觉信息处理相关联的数学模型。我们的重点是将算法结构的表征与大脑神经元所执行的计算联系起来。这些想法的未来实现或许能为开发认知

2 一种受生物启发的运动知觉

运动感知是视觉过程的一种基本特性，它通过短时间内观察一系列不同但相关的图像来实现。灵长类动物的大脑皮层在解剖和功能上可划分为不同的区域，即皮层区域。本节探讨与视觉运动知觉相关的生物学研究，重点关注一个称为中颞区（MT或V5）的小型视觉区域，该区域的神经元对运动感知特别敏感。

运动计算和立体深度感知密切相关。运动方向的计算始于初级视皮层（V1），因为中颞区（MT）的皮层前馈输入来自多个区域，包括V1区以及次级视觉区（ V2）等其他区域。来自V1的输入是最强的[3]。

MT神经元对刺激的朝向、速度和运动方向具有选择性。大多数MT神经元对运动刺激的方向具有选择性。投射到MT区的V1神经元具有方向选择性，即这些细胞对某一特定（偏好）方向的运动反应强烈，而对相反方向或无效方向的运动则反应很弱或几乎没有反应。基本上， MT区的分析可能在与运动感知相关的视觉信息处理中发挥重要作用[4, 5]。

视差选择性已经在投射到MT神经元的V1和V2细胞对水平刺激视差的反应中得到证实[6]。MT区较大的感受野（RF）也对非水平视差敏感，即这些细胞并非专门用于检测水平视差，而是对垂直和水平刺激视差均具有选择性[6]。

中颞区感受野要比之前在[1],中描述的更广泛，因为它们利用了更丰富的信息。皮层MT区神经元感受野的特性大致可分为两个主要部分：中心区域，即所谓的经典感受野（CRF），以及周围区域（图1）。MT感受野具有一些有趣的特性，例如：i) 周围区域远大于经典感受野；ii) 具有拮抗区的中心‐周围感受野关系；iii) 感受野在周围区域呈现圆形对称和非对称表征；iv) 许多感受野沿偏好运动方向轴向伸长[7–11]。

MT细胞的感受野是复杂的结构，无法基于线性机制进行准确建模，因为方向选择性本质上是非线性的。因此，非线性机制对于生成方向选择性[9, 12, 13]至关重要。

已有许多关于运动检测机制的研究，旨在解释方向选择性[14–18]。这些研究受到包括人类在内的多种动物的启发。这些模型基于一个核心理念，即任何运动检测算法都必须完成三项基本计算。运动计算的第一个特定方面是输入刺激，因为我们需要分析至少两条在空间上分离的输入通路，由于运动检测需要比较空间中相邻两点的信号。其次，这两条输入通路的时间滤波必须以某种方式呈现不对称性，否则运动检测机制可以互换而不影响输出结果。第三，由于视觉皮层神经元中的方向计算并非仅靠线性相互作用就能完全解释，因此这两条输入通路必须通过一种非线性机制进行整合[19–22]。

运动计算的早期模型之一是由Hassenstein和 Reichardt提出的[23],，即Re‐
赖希哈特检测器（也称为哈森施泰因‐赖希哈特检测器）。
扩展的赖希哈特检测器，即在基本赖希哈特模型基础上补充了空间感受野的模型，可以解释人类对运动的 psychophysical 反应。Santen 和 Sperling [14]分析了扩展赖希哈特检测器（ERD）与阿德尔森和伯根[16]的运动能量检测器以及沃森和阿瓦达检测器[17]之间的关系。阿德尔森和伯根检测器是带有乘性常数的ERD重构形式。他们将滤波后的输入信号以π/2的空间相位偏移和 π/2的时间相位延迟进行组合。ERD的完全对抗形式的输出信号在形式上等同于时空能量模型。此外，一个扩展的沃森和阿瓦达检测器，包含平方运算、随后的时间整合，以及两个镜像子单元输出的相减，完全等价于具有 π/2时间延迟和空间相位偏移滤波器的ERD。这两种检测器[16, 17],尽管内部结构不同，但相较于ERD的标准形式，都是用于构建方向选择性计算方法的更复杂方式。

神经系统中的神经元相互作用一直启发着算法模型的设计。这些模型通过形式化操作（如卷积、减法、乘法等）来实现运动检测。许多利用生物启发式运动模型的机制研究，采用了现有的运动检测器[16, 17, 23]，以分析适用于多种活动的方向敏感计算（如动作识别、运动透明度、轮廓检测等）。在[24–28]中可以找到一些这类计算机视觉应用的例子，适用于各种真实世界图像序列和合成图像序列。

我们的研究探索了一种基于尚未完全理解的生物学信息的替代方法，即生物运动检测机制如何实现神经元突触相互作用，以及如何执行乘法运算。我们提出了一种模型（图2），用于分析非线性数学运算——指数，以改善细胞的响应。我们在现有的精细设计的修正的 Reichardt 探测器（ERD）[14, 15],基础上，简单地在最后阶段之前增加一个输出指数，其中左向选择性运动探测器的输出从右向检测器的输出中减去。这种在运动处理中的特定适应可显著改变神经元选择性。我们结合这些非线性组件特征，以产生更精确的方向选择性预测 [12, 21, 29–31]。

在改进的ERD之后，后续响应会考虑更大的刺激背景，我们计算fi‐

α 和 (.)β），然后进行减法步骤（+表示异 号求和）。第二阶段以平方运算开始，接着通过高斯滤波器对运动 速度和方向实现速度模糊（Λvel）。之后计算由反馈信号（MT反 馈）增强的信号。端止型单元（ES）被建模为中心细胞响应除以周 围抑制响应的除法运算。第三阶段以平方运算开始，随后使用高斯 函数进行平滑（Λspace），并计算V1区与MT区之间感受野的空间 尺寸差异（f 5:1 interp 为空间插值，用于分辨率降低）。然后再次实现 速度模糊（Λvel）。符号 ÷表示归一化过程。最后恢复原始图像大 小（f 1:5 interp ）)

通过两个阶段产生神经反应（图2）。第一阶段，来自中颞区（MT）的调制反馈（FB）进入反馈阶段，随后计算一个非线性抑制成分，从而形成其较大的感受野。这种抑制在很大程度上是非特异性的，并被建模为端止型单元，这些单元是简单型和复杂型的亚型。具有这种特性（端止）的神经元存在于V1层中，并为MT细胞提供输入。MT细胞的大量输入部分来自端止型单元。另一个阶段通过标准归一化模型来解释细胞特性，以整合MT区运动整合的各种结果。在这两个阶段中，细胞的感受野周围都存在抑制区域，且来自周围区域的影响应被建模为除法性或减法性抑制。在本模型中，中心与周边机制（抑制）之间的相互作用是除法性的。这种发生在经典感受野之外的相互作用有助于改善运动检测的结果[32–36]。

在这项工作中，我们描述了如何通过结合改进的 ERD、端止型单元和归一化来检测运动。这些方法均为受生物启发的处理方案，我们在合成图像序列和真实世界图像序列中对所提出的算法进行了评估。

3 建模光流运动估计

为了推进对视觉区V1和MT神经元如何参与运动感知的理解，我们开发了一个分层建模框架。图2展示了所提出的运动检测算法的基本计算结构。光流处理通过一系列步骤进行计算，我们的架构始于改进的ERDs模型，该模型具有两个输入刺激（图像），并引入简单的时间延迟 （I(x, y, t0) 和 I(x,y,t1)），即在二维图像强度坐标（x,y）上施加时间延迟（t0 和 t1）。因此，为了估计时空相关性，我们采用了两个输入刺激的空间位移（水平和垂直）来定义：
$$
I(x, y, t0) \Delta l,n= I(x −\Delta xl,n, y −\Delta yl,n, t0), \quad (1)
$$
$$
I(x, y, t1) \Delta l,n= I(x −\Delta xl,n, y −\Delta yl,n, t1), \quad (2)
$$
其中 $\Delta xl,n=sl × cos(\delta n)$，$\Delta yl,n=sl ×sin(\delta n)$， $\delta n$为方向角，
$sl$表示运动速度，$n= 1…N_\delta$为运动方向的索引，$N_\delta$为方向数量，$l= 1…N_s$为运动速度的索引，且$N_s$为速度数量。

与神经生理学数据一致，视觉皮层中的许多神经元具有调谐的方向反应特性。如我们之前的工作[1],所述，每个对应于方向选择性神经元的V1感受野通过建模实现线性带通滤波器，即傅里叶域中的一组二维对数‐伽博函数（时间维度未进行傅里叶变换），如下所示：
$$
g(r, \phi; \theta_m,f_h)= \exp\left[-\frac{(\log(r/f_h))^2}{2(\log(k/f_h))^2}\right] \times \exp\left[-\frac{(\phi − \theta_m)^2}{2\sigma^2}\right], \quad (3)
$$
其中$(\phi − \theta_m)$为绝对角度距离，即$(\phi −\theta_m) = |\tan^{-1}( \sin(\theta_m − \phi)/\cos(\theta_m − \phi))| $，坐标系根据方向角 $\theta_m$进行旋转，$m$对应运动方向索引，$\phi= \tan^{-1}(−y/x)$为逆时针角度坐标。高斯函数在角度方向上的标准差 $\sigma$具有恒定值 $\pi/9$（该值基于经验数据）。中心径向频率为$f_h$， $h$对应空间频率索引，$k$是用于确定滤波器在径向方向上带宽的标准差，$r$为径向坐标（$r= \sqrt{x^2+y^2}$）。项$k/f_h$具有固定值0.55，以实现恒定形状比滤波器[37, 38]。

输入图像的傅里叶变换用帽子符号表示，并将变量转换为角频率（时间维度未进行傅里叶变换），即 $I(x,y,t0)$ 被傅里叶变换为$\hat{I}(\omega_x, \omega_y, t0)$。此处，每个输入刺激均通过log‐Gabor函数进行滤波，然后得到如下计算信号（四种可分离组合输出）：
$$
A(x, y, t0; \theta_m,f_h)= F^{-1}{\hat{I}(\omega_x, \omega_y, t0) \times g(r, \phi; \theta_m,f_h)} \quad (4)
$$
$$
A’(x, y, t0; \theta_m,f_h) \Delta l,n= F^{-1}{\hat{I}(\omega_x, \omega_y, t0) \Delta l,n \times g(r, \phi; \theta_m,f_h)} \quad (5)
$$
$$
B(x, y, t1; \theta_m,f_h)= F^{-1}{\hat{I}(\omega_x, \omega_y, t1) \times g(r, \phi; \theta_m,f_h)} \quad (6)
$$
$$
B’(x, y, t1; \theta_m,f_h) \Delta l,n= F^{-1}{\hat{I}(\omega_x, \omega_y, t1) \Delta l,n \times g(r, \phi; \theta_m,f_h)} \quad (7)
$$
其中符号$F^{-1}$对应于逆傅里叶变换。

滤波刺激输出在空间域中通过时间的逆傅里叶变换计算 $t0$（4）与来自时间延迟（t1）并带有空间位移（7）的直接输入相关。这可以通过局部图像相位（$\psi_{A_{m,h}}= \arg{A(x, y; \theta_m,f_h)}$和 $\psi_{B’ {,\Delta l,n {m,h}}} = \arg{B’(x, y; \theta_m,f_h)\Delta l,n}$）。我们考虑时间顺序的变化 （第9卷），其中（5）与（6）通过局部图像相位（$\psi_{A’, \Delta l,n_{m,h}} = \arg{A’(x, y; \theta_m,f_h)\Delta l,n}$ 和 $\psi_{B_{m,h}}= \arg{B(x, y; \theta_m,f_h)}$）相关。因此，我们将相关方程定义如下：
$$
C_{AB’}^{l,n}= \frac{1}{N_\theta} \sum_{m=1}^{N_\theta} [\cos(\psi_{B’,\Delta l,n_{m,h}} − \psi_{A_{m,h}})] + \quad (8)
$$
$$
C {BA’}^{l,n}= \frac{1}{N_\theta} \sum_{m=1}^{N_\theta} [\cos(\psi_{B_{m,h}} − \psi_{A’,\Delta l,n_{m,h}})] + \quad (9)
$$
其中$N \theta$是方向数量，$[.]_+= \max(., 0)$表示正半波整流，因为细胞不能产生负值。随后，对不同方向的相关结果进行求和。

方程(8)和(9)用于描述V1区复杂细胞响应的基本思想涉及复数运算，即对应于复值对数‐伽博滤波器（相位正交）的实部（Re）和虚部（Im）的响应（简单细胞）之和。我们考虑每个4个响应式(4)‐(7)的实部和虚部，因此在复平面上共有8个测量值。在此条件下，如果我们重写图像相位间角度差（正交）的余弦表达式(8)和(9)，可以看出：
$$
C_{AB’}^{l,n}= \frac{1}{N_\theta} \sum_{m=1}^{N_\theta} \left{ \text{Re}[A(x, y, t0; \theta_m,f_h)] \times \text{Re}[B’(x, y, t1; \theta_m,f_h) \Delta l,n] + \text{Im}[A(x, y, t0; \theta_m,f_h)] \times \text{Im}[B’(x, y, t1; \theta_m,f_h) \Delta l,n] / |A(x, y, t0; \theta_m,f_h)| \times |B’(x, y, t1; \theta_m,f_h) \Delta l,n| \right} +, \quad (10)
$$
$$
C {BA’}^{l,n}= \frac{1}{N_\theta} \sum_{m=1}^{N_\theta} \left{ \text{Re}[A’(x, y, t0; \theta_m,f_h) \Delta l,n] \times \text{Re}[B(x, y, t1; \theta_m,f_h)] + \text{Im}[A’(x, y, t0; \theta_m,f_h) \Delta l,n] \times \text{Im}[B(x, y, t1; \theta_m,f_h)] / |A’(x, y, t0; \theta_m,f_h) \Delta l,n| \times |B(x, y, t1; \theta_m,f_h)| \right}_+, \quad (11)
$$
其中 ×和/分别表示对每个矩阵元素进行乘法和除法运算。
该公式化表述与[39, 40]的假设一致。

改进的ERDs模型通过引入扩展的静态输出非线性 （α和 β）而完成，相关非对称输出中的减法操作如下所示：
$$
C(x, y, \delta_n, s_l)=[(C_{AB’}^{l,n})^\alpha −(C_{BA’}^{l,n})^\beta]_+. \quad (12)
$$
在下一级（第二阶段——图2）中，对应于皮层V1区，采用了一种基于三个步骤的级联架构，涉及空间整合、信号增强、反馈信号（反馈信号）重新进入以及归一化 （中心‐周围区域分流抑制）。

运动信号的整合是一个渐进的过程，其基本思想由非线性常微分方程构成。这些方程考虑了膜特性以及归一化增益控制。神经细胞的电学特性可以用电路来表征。细胞膜被建模为一个电阻和一个电容，即RC电路。皮层细胞的行为类似于RC电路，而输入到细胞的电流则由随时间变化的突触电导驱动[41–43]。根据该模型，膜电路的动力学遵循以下方程：
$$
\tau \dot{x}= −D × x+(x −E_{ex}) × g_{ex} −(x −E_{in}) × g_{in}, \quad (13)
$$
假设静息状态为零水平，且漏电导恒定$g_{leak}= D$； $\tau$表示膜时间常数，$x$为细胞的膜电位。项$g_{ex}$和$g_{in}$分别表示来自兴奋性和抑制性神经元突触的总输入。参数$E_{ex}$和$E_{in}$分别定义兴奋性和抑制性电导的反转电位。

神经元模型的实现将这些机制整合到三个连续的通用计算步骤（14）‐（16）中，这些步骤是膜（13）[44–48]的变体：
$$
\dot{x}^{(1)}= −x^{(1)}+(x_{FF})^2 * \Lambda_{vel}, \quad (14)
$$
$$
\dot{x}^{(2)}= −x^{(2)}+ x^{(1)} ×(1+ F × x_{FB}), \quad (15)
$$
$$
\dot{x}^{(3)}= −x^{(3)}+ x^{(2)} −(G+ H × x^{(3)}) ×\sum x^{(2)}, \quad (16)
$$
其中，$x^{(1)}$、$x^{(2)}$ 和 $x^{(3)}$ 表示特定模型区域三个阶段内的活动。参数 $x_{FF}$ 表示驱动输入信号（前向流）。 $\Lambda_{vel}$ 表示用于滤波操作的加权核（速度模糊）。项 $x_{FB}$ 是调制反馈信号，常数 $F$ 调整反馈强度。常数 $G$ 和 $H$ 控制归一化的强度。

V1区神经动力学实现特征提取的机制表现出端止特性在一定程度上影响单元。我们借鉴文献中关于端止型单元特性的若干指标来估计运动[32, 35, 36]。我们遵循 (14)‐(16)中的神经三级处理机制：首先进行非线性信号增强，即对信号进行平方处理以锐化分布；然后通过不同的高斯核（$\Lambda_{vel}$）分别对运动速度和运动方向 [39, 44, 47, 49]进行速度模糊处理。
$$
\dot{x} {v1}^{(1)}= −x {v1}^{(1)}+(x_{FF}^{v1})^2 * \Lambda_{vel}, \quad (17)
$$
其中$x_{FF}^{v1}= C(x,y, \delta_n, s_l)$，$x_{v1}^{(1)}$的取值范围为0到1之间，模糊通过在速度域中与高斯函数进行卷积（*）计算得到，该高斯函数的标准差对于运动速度为 $\sigma_s= 0.2$像素每帧，对于运动方向为 $\sigma_\delta= 0.75$。速度采用对数尺度编码。

运动信号整合为视觉系统所采用的处理过程提供了重要线索。皮层区域中存在一种称为循环连接的机制，而V1区的周边抑制受到来自MT的反馈影响。反馈连接在处理视觉信息时能够增强与运动方向一致的相干输入，从而有助于向其他皮层视觉区域进行信息提取的过程。MT在V1[44, 47, 50–53]区域的运动信号整合中起着重要作用。我们的模型包含了V1和MT之间的双向连接。V1 中的反馈信号（FB）按如下方式计算：
$$
\dot{x} {v1}^{(2)}= −x {v1}^{(2)}+ x_{v1}^{(1)} ×(1+ F × x_{FB}^{v1}), \quad (18)
$$
其中F的固定值为100，用于放大反馈信号（$x_{FB}^{v1}$），且 $x_{v1}^{(2)}$在零到一之间取值。

端止模型可作为我们MT模型的合适前端。我们在考察端止特性时，并不认为这些神经元在V1中构成一个独立的类别，因为许多V1神经元表现出一定程度的端止特征，即来自周围区域的抑制性影响。在此，我们展示了另一种形式的端止单元，该单元通过将非经典感受野结构的分析扩展到初始运动检测器的输出来实现。因此， V1细胞的响应可以通过对中心‐周围相互作用的分析所揭示的除法归一化（分流抑制）来表征[32, 35, 36, 39]。在反馈信号步骤之后，基于方程(16)的稳态解，利用V1中已知存在的机制对运动信息编码的过程可近似如下：
$$
x_{v1}^{(3)}= \frac{r_{center}}{\epsilon+ r_{center}+ k r_{surround}}, \quad (19)
$$
其中$r_{center}$为中心细胞的响应，通过使用狄拉克脉冲进行滤波来近似（$r_{center}=x_{v1}^{(2)}$—不应用核函数）。$r_{surround}$是通过将信号$x_{v1}^{(2)}$与高斯滤波器进行卷积计算得到的总周围区域响应，其参数值为运动速度 $\sigma_s= 0.5$像素每帧，运动方向 $\sigma_\delta= 2.0$。该模型基于感受野中心和周围区域在空间上重叠的假设，因此周围交互会覆盖中心并对其产生抑制作用。常数k为增益参数（设为5）， $\epsilon$的固定值为 1。

运动是多种生物相关信号的丰富来源。V1区的活动影响着方向信息的知觉解释，而中颞区（MT）从V1区域继承了大量方向信息。我们提出，下一阶段（第三阶段——图2）由皮层MT区完成。我们再次遵循(14)‐(16)中的三步处理过程：首先，来自V1的信号被平方以实现非线性信号增强；接着进行空间整合（$\Lambda_{space}$），其中信号与高斯核进行卷积，随后使用线性插值（$f_{5:1}^{interp}$）进行采样（以获得不同的空间分辨率）。这种较低的空间分辨率（信号更少歧义）与传入MT的视觉输入及其相比 V1[5, 44, 47]更大的感受野大小相一致。然后，如同第二阶段一样，运动信号在速度域（$\Lambda_{vel}$）中被平滑处理，并采用与V1区域相同的参数。随后，我们按如下方式计算整合结果：
$$
\dot{x} {MT}^{(1)}= −x {MT}^{(1)}+f_{5:1}^{interp}((x_{FF}^{MT})^2 * \Lambda_{space}) * \Lambda_{vel}, \quad (20)
$$
其中$x_{FF}^{MT}= x_{v1}^{(3)}$和$x_{MT}^{(1)}$的取值范围在0到1之间。空间分辨率降低了5倍（线性插值），标准差为 $\sigma_{space}= 5$，对应$\Lambda_{space}$。

如果我们的模型包含了其他皮层区域（如中上颞区 （MST））的影响，那么MT区域的反馈信号可以被纳入考虑。然而，在当前涉及V1区和MT之间连接的模型中，MT中的反馈信号计算如下：
$$
\dot{x} {MT}^{(2)}= −x {MT}^{(2)}+ x_{v1}^{(1)} ×(1+ F × x_{FB}^{MT}), \quad (21)
$$
其中，反馈信号 $x_{FB}^{MT}$不接收任何输入，且$x_{MT}^{(2)}$的取值范围在零到一之间。因此，其稳态下的结果响应由恒等式 $x_{MT}^{(2)}= x_{MT}^{(1)}$表示。

如图2所示，视觉系统机制的活动细节表现为通过视觉区域层级结构进行处理步骤的顺序细化。MT细胞在整合和解释前一级输入中起着重要作用末端停止细胞（V1）。为了分析视觉运动，MT神经元的对抗性是一个关键方面。我们认为抑制有助于MT神经元的速度和方向调谐。我们通过应用中心‐周边相互作用来拟合除法抑制，其中MT神经元由兴奋性和抑制性成分构成，表现出归一化特性。更重要的是，该细胞模型产生的是具有除法性质的非特异性抑制。中心与周边在大小上不同，兴奋性成分被定义为每个$x_{MT}^{(2)}$的输出，而周围区域计算所有速度的总和[33, 34, 54]：
$$
\dot{x} {MT}^{(3)}= \frac{x {MT}^{(2)}}{\sigma^2_{MT}+\sum x_{MT}^{(2)}}, \quad (22)
$$
其中$\sigma_{MT}= 0.01$。方程(22)基于(16)的稳态解。

最后，如图2所示，通过线性插值（$f_{1:5}^{interp}$）来重建原始图像尺寸。

速度估计基于具有不同方向（$\delta_n$）和速度（$s_l$）的相似空间感受野，即在每个空间位置上的一组假设。这些可能的集合可被解释为局部神经群体编码，这与中颞区细胞的生物学特性相吻合。为了找到最佳匹配，我们可以利用除法归一化方法对由单元群体组成的局部运动信息进行汇集，以确定最活跃的神经元。因此，为了在给定空间位置上解释运动群体，我们只需进行归一化，从而呈现单一激活信号[55–57]：
$$
R_{norm}= \frac{\sum M_{vel} × x_{MT}^{(3)}}{\sum x_{MT}^{(3)}}, \quad (23)
$$
其中$M_{vel}$表示对细胞速度进行调谐的结果（+$\Delta xl,n$和 −$\Delta yl,n$）。

用于估计真实和合成图像序列运动的特定参数将在下一节根据已实现的测试给出。

4 实验结果

所描述的光流技术已实现，并应用于多种真实图像序列和合成图像序列。实验评估采用了来自Middlebury光流库（vision.middlebury.edu/flow/）[58, 59]和[60]的灰度合成图像及真实世界图像作为输入。我们考虑了真实世界图像，即使用相机，由真实物体和自然纹理组成。合成图像是使用计算机图形生成的人工序列，其中一些使用真实图像来创建表面纹理。

我们使用角度误差度量进行定量比较，同时也计算绝对误差。定量计算理论可以有效总结现有数据，并帮助我们检验计算模型的一致性。在评估时（参见附录A），我们采用了平均角度误差（AE）和绝对光流终点误差（EE）[58–62]。

我们几乎使用了[47]中的所有相同参数值。对于对数‐伽博滤波器，其方向为 $\theta_m=m\pi/N_\theta$，其中$N_\theta= 8$是方向数量（$m = 1… N_\theta$）。空间频率定义为$f_n= 1/(2\pi/(sw s_1 s_Nf −h b))$，其中$sw= 3.0$将角频率与速度相关联，$s_1= 0.8$是最小速度，$s_b$是影响滤波器之间重叠的因子（$h = 1… N_f$，$N_f= N_s − 1$，$s_b= 1.5$）。对于低速图像序列（Army、Mequon、Schefflera、Wooden、 Yosemite、Rubber‐Whale、Hydrangea、 Dimetrodon、Grove2、Grove3、Translating tree和 Diverging tree），速度数量为$N_s= 7$。对于高速图像序列，Grove、Urban、Teddy、Urban3使用$N_s= 9$， Urban2使用$N_s= 10$。速度是最小速度的倍数，最小速度定义为($s_l=(sw s_1 s_l−1 b)/sw$)，其中$l = 1… N_s$。方向为$\delta_n= n2\pi/N_\delta$，其中方向数量为$N_\delta= 16$（$n = 1… N_\delta$）。此外，所使用的第一速度和第一频率均为零。运动计算使用5帧。对于Middlebury光流库，我们使用第7到11帧（除非序列仅提供两张图像），而对于[60]，我们使用第17到21帧。

用于速度模糊和周围交互的运动方向高斯核分别在 3x1和9x1像素的区域内计算。用于速度模糊和周围交互的运动速度高斯核采用对数尺度编码，并且两个滤波器均在1x5的区域内计算。空间整合($\Lambda_{space}$)的高斯核在 21x21像素的区域内计算。对于高斯滤波，我们使用两种边界条件：运动方向域采用圆形边界条件，运动速度和空间域采用复制边界条件。

表1 和 表2 分别展示了我们的算法在具有隐藏真实光流（数据集1）和公开真实光流（数据集2）的光流数据集上的性能。在我们的实验中，除了原始配置外，我们还比较了另外两种针对相同输入序列的配置（表2）。首先，为了检验指数（$\alpha$ 和 $\beta$ ——图2）的重要性，我们执行不使用它们的算法。然后，为了评估从中颞区到V1区的反馈信号对算法的影响，我们执行不带反馈信号的算法。

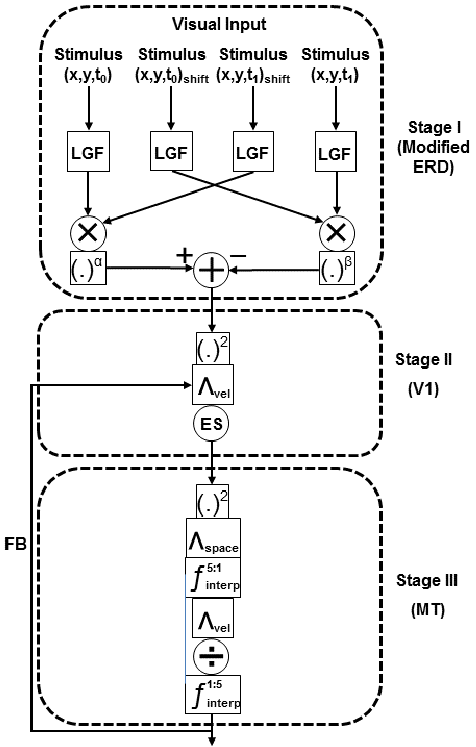
表1 ：合成与真实世界图像序列（数据集1）的运动感知估计误差统计。

序列	平均误差	均方根
Army	8.97	0.24
梅昆	8.89	0.88
鹅掌柴	10.9	1.08
木制的	8.30	0.78
树林	8.16	2.0
城市	22.9	3.09
泰迪	19.9	3.81

表2 : Errorst 针对多种合成与真实世界图像序列（数据集2）的运动感知估计的统计误差

序列	我们的方法 平均误差	均方根	我们的方法不包含 指数 $\alpha$和 $\beta$ 平均误差	均方根	我们的方法不包含 来自MT的FB 平均误差	均方根
RubberWhale	6.59	0.22	7.87	0.26	6.91	0.23
绣球花	5.36	0.55	8.75	1.18	5.67	0.71
异齿龙	4.31	0.27	11.46	0.71	4.31	0.27
树林2	5.98	0.50	9.50	0.88	9.14	0.75
林区3	11.84	1.37	15.76	1.98	14.68	1.70
城区2	22.61	3.11	35.05	6.51	29.38	5.18
城区3	18.91	3.09	29.38	5.19	28.91	4.72
金星	12.96	1.25	21.47	2.21	12.96	1.25
优胜美地	5.43	0.28	8.71	0.46	7.34	0.41
翻译树	1.33	0.09	3.75	0.23	1.81	0.11
发散树	5.58	0.16	8.00	0.24	5.31	0.15

表3 : 我们的模型与文献中一些最先进的生物启发方法在平均角度误差上的比较。

序列	我们的方法	Raudies 2012a	Solari 2014b	Dellen 2011c	Solari 2015d
橡胶鲸鱼	6.59	-17.1	9.8	10.20
绣球花	5.36	–9.3	5.96
异齿龙	4.31	----
Army	8.97	14.5	–	12.0
梅昆	8.89	11.4	–	10.7
鹅掌柴	10.9	16.8	–	15.6
木制的	8.30	11.7	–	16.6
树林	8.16	16.6	–	6.51
树林2	5.98	—		4.28
林区3	11.84	—		9.72
城市	22.9	27.3	–	16.2
城区2	22.61	—		14.51
城区3	18.91	—		15.11
优胜美地	5.43	9.77	11.4	3.75	3.41
翻译树	1.33	–	0.52	-
发散树	5.58	-6.7	3.82	-
金星	12.96	----
泰迪	19.9	37.9	–	12.3

a [47] b [63] c [64] d [65]

图3和图4展示了三个真实图像序列（梅昆、鹅掌柴和木制的）、两个合成图像序列（树林和城市）以及一个修改后的立体数据（泰迪）的估计的光流。在最左列中，我们看到的是flowcolorcoding，即用颜色编码的真实光流，用于表示速度和方向（Middlebury彩色编码）。它将每种可能的速度对应一种单一颜色，速度的方向对应颜色的色调（速度越慢颜色越白）。我们在图3和图4中包含了表1中所展示结果的图像。

图5和图6分别显示了三个真实图像序列（ RubberWhale、Hydrangea和异齿龙）以及三个合成图像序列（树林2、优胜美地和发散树）的估计的光流。在最左列中，我们看到光流的颜色编码（Middlebury彩色编码）。我们在图5和图6中包含了表2中所示结果的图像。

该算法的性能可与某些最先进的生物启发方法获得的[47, 63–65]相媲美。文献中存在多种方法仅测试了广泛使用的简单合成优胜美地序列及其真实光流，这非常有限。我们的研究重点是与进行了多项测试的研究结果进行比较。根据表3，所提出的算法在[47, 63]中的估计光流结果优于现有结果。

除了泰迪和金星是立体图像对之外，与[64, 65]中给出的结果相比，我们提出的算法在真实世界图像（表3的前七幅图像）上的平均角度误差结果优于合成图像。

总结结果，模拟表明，额外的非线性组件（指数）以及MT细胞向V1区的反馈投射能够产生更精确的运动检测结果。

5 讨论

我们的模型受到之前工作[1]的启发，其中我们通过对数伽博函数表示V1细胞的感受野。尽管我们之前的方法[1]使用能量模型[16]来描述复杂细胞的结构，但在本研究中，我们选择修正的 Reichardt 探测器[14, 23]从输入图像序列中提取运动信息。我们选用修正的 Reichardt 探测器来计算运动，因为能量模型[16]实际上是修正的 Reichardt 探测器的一种更复杂的重新表述。这种生物学上合理的模型更容易配置，并且使我们能够在 MATLAB中开发出具有合理处理时间的算法。我们花费了165秒来获得优胜美地序列的估计的光流（图6）。

V1神经元模型是对修正的 Reichardt 探测器的一种相对简单的扩展，其定义在公式中使用了指数。表2展示了我们的算法在不包含指数（$\alpha$和 $\beta$）情况下的结果。如果我们将其与所提出算法的结果（表2）进行比较，可以观察到引入到修正的 Reichardt 探测器结构中的非线性相互作用有助于改善输出数据。

为了检验从中颞区到V1区的反馈连接的重要性，我们在没有反馈信号的情况下测试了我们的算法（表2）。我们的结果表明，反馈信号对合成序列的相对性能的影响大于对真实世界图像的影响。

我们提出了一种基于V1区域中抑制性中心‐周边相互作用的不同实现方式，依据是一些证据表明端止型单元可以调节周围区域的抑制[32, 33, 35]。这种解释具有吸引力，因为非特异性抑制可能来源于多种细胞的组合[33]，而我们将这些延伸至经典感受野之外的特性建模为除法归一化。

该算法在包含运动不连续性、刚性与非刚性运动、隐藏纹理、细长结构、低纹理区域和阴影的真实世界图像（Army、Mequon、Schefflera、Wooden、 RubberWhale、Hydrangea 和 Dimetrodon）上表现良好[59]。针对真实世界图像中的光流计算，选用了最优拟合参数值。另一方面，我们的方法在包含大位移运动的合成图像序列上存在局限性。实验结果部分[64, 65]中提到的生物启发方法需考虑的一个方面是：它们在合成图像上效果较好，但在真实图像上的性能较差。这是由于现有结果中出现的过度平滑序列所导致的。生物启发模型面临的一个挑战是，寻找有效的方法，以准确地在基准测试[59]的不同数据类型中提取运动信息。

总之，本研究提出了一种生物启发模型，该模型采用带有幂运算、来自MT的反馈以及影响V1神经元的分流抑制（端止型单元）的改进的ERD。V1的输出馈入 MT神经元，空间分辨率降低，随后进行归一化和池化以找到运动检测中最活跃的神经元。我们的模型与已知的 V1区和MT脑区神经元特性一致，并提出了有序排列和方法组合，这不同于现有的最先进方法。

作为未来工作，我们正考虑通过增加一个阶段来扩展所提出的模型，以表征V2神经元，从而研究整体结果是否可以得到改善。这项研究可以回答V2神经元的特性是否与MT神经元相似，以及它们是否能够通过一种高度非线性的整合机制[3, 66]来整合信号信息。