深入理解卷积神经网络（CNN）：原理与应用

随着深度学习的迅猛发展，卷积神经网络（Convolutional Neural Network, CNN）已经成为计算机视觉和图像处理领域的核心技术之一。本文将深入探讨卷积神经网络的基本原理、结构组成、关键特性，以及其在实际应用中的表现。

一. 卷积神经网络的基本原理

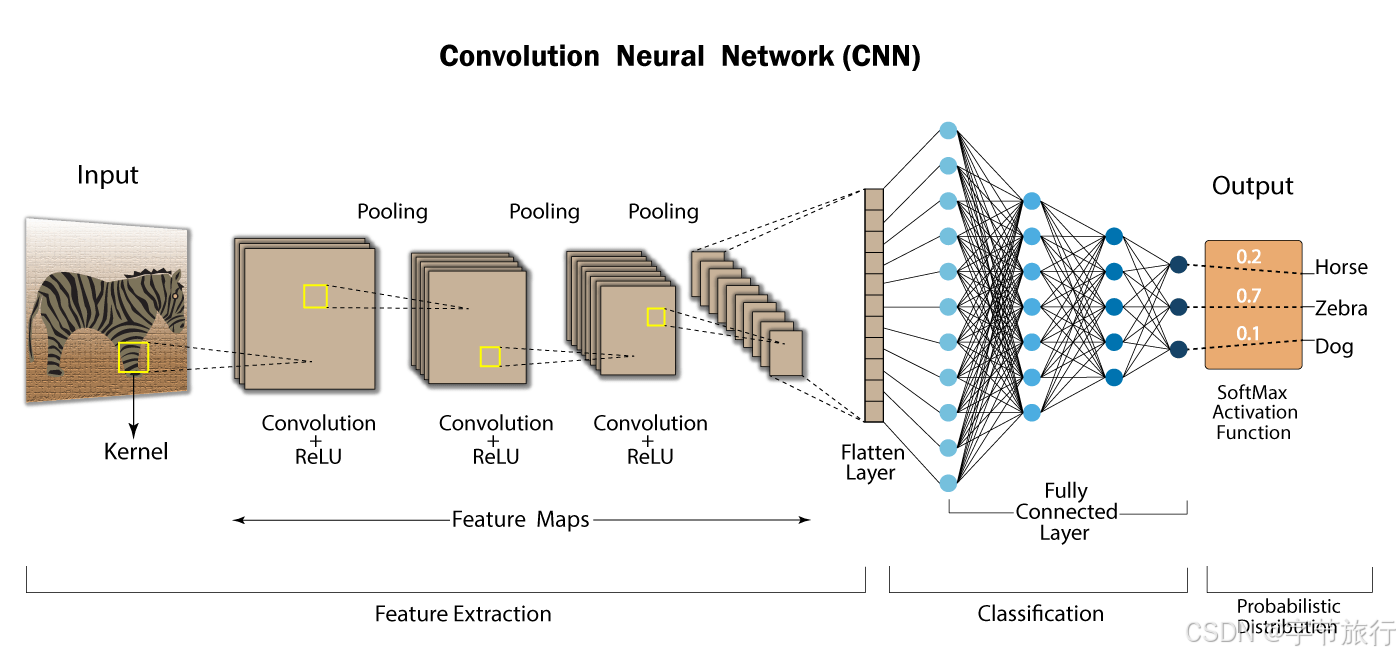
卷积神经网络（CNN）是在传统神经网络基础上发展而来的一种深度学习模型，特别适合于处理图像、音频和其他具有网格结构的数据。其基本原理可以从生物视觉系统的结构中找到灵感。CNN的设计意在模拟人类的视觉处理方式，通过不同的层次逐步提取和分析特征，使得网络能够有效地从原始输入中学习到有用的信息。

1.1 卷积操作

卷积神经网络的核心在于“卷积”操作，这是CNN与其他神经网络的重要区别所在。卷积过程涉及一组学习到的过滤器（也称为卷积核），它们在输入数据（如图像）上滑动，进行局部区域的点积运算。具体来说，卷积运算可以用以下公式表示：

其中，I表示输入图像，K表示卷积核，x和y是卷积核在图像上滑动的坐标。

1.1.1 卷积核

卷积核是一个较小的矩阵，其大小通常较小（例如3x3或5x5），功能是提取局部特征。每个卷积核会学习到特定的特征，比如边缘、颜色梯度、纹理等。当多个卷积核同时应用于同一图像时，模型可以提取出丰富的特征信息。随着层数的增加，卷积核的数量也将逐步增加，从而捕捉越来越复杂的图像特征。

1.1.2 步幅与填充

在卷积操作中，步幅（Stride）和填充（Padding）是两个重要的参数。步幅定义了卷积核在输入图像上移动的步长，较大的步幅会导致输出特征图的尺寸减小。填充是指在输入数据的边缘添加额外的像素，目的是为了控制特征图的尺寸，并防止信息的丢失。常用的填充方式有“有效填充”（valid padding）和“同等填充”（same padding）。

1.2 激活函数

在卷积层之后，通常会使用激活函数来引入非线性。非线性是深度学习模型的基本特性之一，它使得模型能够学习到复杂的函数映射关系。常见的激活函数包括ReLU（Rectified Linear Unit）、Sigmoid和Tanh等。

• ReLU函数的定义为：

  

  ReLU函数在正区间保持线性，在负区间输出零，从而有效地解决了梯度消失的问题，促进了模型的收敛加速。

• Sigmoid函数将输入映射到0到1之间，使其在概率任务中特别有用，如二分类问题，但在深层网络中仍然可能导致梯度