1. 引言:Excel 的“一键魔法”背后藏着什么智慧?
在 Excel 中,我们只需右键 → 添加趋势线,一条完美的直线就出现了。它快得像魔法,但魔法背后,是数学的严谨。
今天,我们不关心 Excel 内部用了什么算法(可能是解析法),而是要问:
如果机器一开始‘什么都不知道’,它该怎么一步步‘学会’画出这条线?
2. 我们的任务:预测一个简单的线性关系
假设我们有一组数据,它们大致遵循 y = 2x + 1 的规律,但有一些随机噪声(模拟真实世界的测量误差)。
我们的目标:仅凭这10个数据点,让机器“学会”这个规律,找到最佳的 a(斜率)和 b(截距)。
3. 准备数据:10 个“玩具”样本
我们用 Python 生成这10个数据点:
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子,保证结果可复现
np.random.seed(42)
# 生成 10 个 x 值,从 1 到 10
x = np.arange(1, 11) # [1, 2, 3, ..., 10]
# 生成 y 值:y = 2x + 1 + 噪声
true_a, true_b = 2, 1
noise = np.random.normal(0, 0.5, size=x.shape) # 添加标准差为 0.5 的高斯噪声
y = true_a * x + true_b + noise
# 查看数据
print("x:", x)
print("y:", np.round(y, 2)) # 保留两位小数输出:
x: [ 1 2 3 4 5 6 7 8 9 10]
y: [ 3.25 4.93 7.32 9.76 10.88 12.88 15.79 17.38 18.77 21.27]关键点:真实规律是
y = 2x + 1,但数据有噪声,所以 y 值不完全精确。
4. 可视化:我们的目标是什么?
让我们画出这些数据点,并标出真实的线(y=2x+1):
plt.figure(figsize=(8, 6))
plt.scatter(x, y, color='blue', label='真实数据点', s=50)
# 画出真实规律的线
x_line = np.linspace(0, 11, 100)
y_line = true_a * x_line + true_b
plt.plot(x_line, y_line, 'g--', label=f'真实规律 y={true_a}x+{true_b}', linewidth=2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('我们的“学习”任务:根据10个数据点,找到最佳拟合线')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
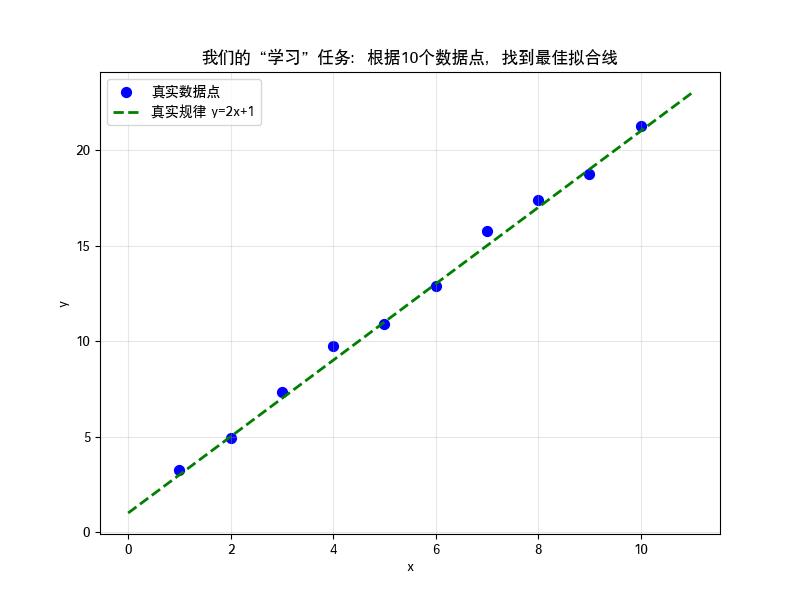
我们的任务就是:仅从这些蓝色散点,让机器找到一条最接近绿色虚线的直线。
5. 模型定义:y_pred = a * x + b
我们假设模型的形式是:
y_pred = a * x + ba:斜率(slope)b:截距(intercept)- 初始时,我们不知道
a和b是多少,可以先猜一个值,比如a=0, b=0。
6. 损失函数:我们“错”了多少?
我们需要一个“尺子”来衡量预测的好坏。用均方误差 (MSE





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 24
24

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








