双差分有源电极设计与分析

双差分肌电图有源电极的分析与简单电路设计

摘要

本文对用于双差分（DD）表面肌电信号（sEMG）测量所需的电压放大器进行了分析，并提出了一种新颖且极为简单的双差分有源电极电路设计。独立的双差分有源电极所需的三输入放大器本质上不同于差分放大器，相关设计知识在现有文献中较为匮乏。首先，通过将输入信号分解为三个正交模式，定义了该放大器的优值指标。该分析揭示了一种包含肌电串扰分量的模式，双差分电极应抑制该模式。接着，分析了有限输入阻抗的影响。由于存在三个端子，获得了具有两个自由度的由电极和输入阻抗不平衡引起的干扰抑制比的最小下限。最后，提出了一种新型电路设计，仅包含一个四运放和少量无源器件。该设计复杂度接近分支电极，远低于采用三个仪表放大器的设计，同时通过为每个电极输入使用单位增益缓冲器，实现了鲁棒的肌电串扰抑制和更优的输入阻抗。本文还分析了该输入级的干扰抑制极限，描述了提出的电路的可复现实现方法，并提供了参数设计指南以根据具体需求进行调整。该电极与现有替代方案进行了比较，并在不同身体部位使用干电极接触采集了表面肌电信号样本，成功抑制了干扰源。

索引词

有源电极, 生物医学传感器, 双差分电极, 干电极, 表面肌电图

一、引言

SURFACE表面肌电信号（sEMG）能够以非侵入式方式获取肌肉活动信息，仅需将电极放置在皮肤上即可测量肌电图信号。电极采集的表面肌电信号的一个理想特性是无串扰，即信号应仅对应于电极正下方肌肉的活动，而不包含其他肌肉活动的串扰分量。串扰分量可能会通过改变触点数量和电极的几何结构，可实现衰减[1],[2]。

已提出多种复杂度逐渐增加的拓扑结构，其中所谓的线性双差分或仅称为双差分拓扑（DD）在保持相对低复杂度的同时，表现出良好的选择性[3]–[5]。该电极被用于研究，并已集成于商用设备（奥托博克13E200，德尔西斯 DE‐3.1）中。

双差分拓扑由三个串联的电极组成，其电位分别为 $ V_A $、$ V_B $ 和 $ V_C $，如图1(a)所示。该电极的输出 $ V_{DD} $ 是两对电极之间差值的差，由以下公式给出：
$$
V_{DD} = (V_B - V_A) - (V_C - V_B) = 2V_B - V_A - V_C \quad (1)
$$

对于许多应用，尤其是需要频繁使用的康复设备、脑机接口（BCIs）或可穿戴生物医学传感器，电极应易于放置、佩戴舒适且维护成本低。当无需使用凝胶且电极无拆卸部件时，最能满足这些要求，而无膏或“干”电极[9],[10]最符合这些条件。特别是对于带来低串扰的配置而言，这尤其重要。

接触板距离更近时，涂抹的凝胶可能会从电极下方溢出并导致短路，因此在这些应用中更推荐使用无膏电极[11]。

然而，干电极的接触阻抗高于湿电极[12]，这使得它们更容易受到电磁干扰（EMI）的影响，相关效应在文献中已有深入分析[13],[14]。因此，需要在电极本身集成缓冲级，从而形成“有源”电极。理想的有源电极具有很高的输入阻抗和低输出阻抗，从而使采集系统对电源线干扰和高电极‐皮肤阻抗具有很强的鲁棒性[15]。电极还应具有低质量以避免运动伪影[16]，这也促使系统设计趋向低复杂度。

获取双差分输出的一种方法是对双极或单极通道的信号进行数字处理，如图1(b)所示。这种方法通常用于肌电电极阵列，因为需要关注不同的信号组合。但对于具有固定几何结构的独立电极而言，这会显著增加系统的复杂性。

也可以仅使用一个仪表放大器（IA）或更简单的实现方式来获取肌电信号的双差分输出，例如在[17]中所见的采用图1(c)所示“分支电极”结构的方法。这种方案非常简单，但其输出仅在电极‐皮肤阻抗完全平衡时才等于双差分输出，而这一点很难保证。一种始终能提供双差分信号的更优模拟解决方案是图1(a)所示的三仪表放大器电路。然而，这种方法增加了元件数量和供电电流，并且具有不平衡输入阻抗，会降低共模抑制比。

双差分信号测量前端的设计通常作为肌电信号分析相关研究的附属内容被提出。最早的实例与肌纤维传导速度的估计有关，见于[18]及其引用的文献中。这些以及后续的实现方案均由独立的差分放大器组合而成，或采用图1中所述的某些替代形式。据作者所知，在现有文献中尚未提出其他独立的表面肌电双极导联有源电极实现方案。此外，尽管双差分电极作为肌电信号换能器的特性已被充分分析（例如，[19],[20]），但针对其所需要的三输入放大器的分析却鲜有研究。该电路显然不同于传统的两输入差分放大器，必须对其进行适当的分析，以明确其在肌电测量中所关注的干扰抑制特性。

本文提出了一种针对双差分放大器的分析，重点研究其干扰抑制能力，并揭示了一种串扰干扰模式。我们提出了一种双差分有源电极实现方案，其复杂度几乎与分支电极相当，同时满足（1）不受电极‐皮肤阻抗影响的特性。该方案仅需一个四运放（OA）和少量无源器件即可实现，非常适合用于构建低成本紧凑型干式有源电极。

II. 双差分电压放大器

A. 优值指标

将双端口的差分和共模信号分解方法无法直接应用于双差分电压放大器。然而，可以通过将三个输入信号转换为三种适用于分析肌电图测量的信号模式来扩展这一概念。

这两种模式源于预期的肌电图测量特性，类似于传统的差分模式和共模模式。其中一种是感兴趣信号，由公式(1)给出，定义为“双差分模式”（DDM）；另一种则代表了大部分电磁干扰信号。因为在简化的电磁干扰模型中，人体被视为等电位体[14]，该干扰电压在三个输入节点上相等，因此该模式可定义为共模（CM）信号。

将第三种模式定义为与双差分模式（DDM）和共模（CM）正交的投影，以便使其效应与感兴趣的信号和电磁干扰（EMI）解耦，这样更为方便。因此，第三种模式被定义为“简单差分模式”（Simple Differential Mode, SDM），以区别于二端口电路中的差分模式。整个分解过程可用以下方程表示：
$$
\begin{bmatrix}
V_{DDM} \
V_{CM} \
V_{SDM}
\end{bmatrix}
=
\begin{bmatrix}
-1 & 2 & -1 \
1 & 1 & 1 \
1 & 0 & -1
\end{bmatrix}
\begin{bmatrix}
V_A \
V_B \
V_C
\end{bmatrix}
\quad (2)
$$

每种模式对输出的贡献可以用如下定义的适当传递函数来表示：
$$
G_{DDM} = \frac{V_{out}}{V_{DDM}}, \quad G_{CM} = \frac{V_{out}}{V_{CM}}, \quad G_{SDM} = \frac{V_{out}}{V_{SDM}} \quad (3)
$$

由于电磁干扰在所有输入节点上均等存在，且不包含目标信号，因此SDM中没有显著的EMI干扰信号。所以，双差分放大器的共模抑制比可以简单定义为 $ CMRR = 20 \log_{10} \left| \frac{G_{DDM}}{G_{CM}} \right| $。

然而，简单差分模式（SDM）确实包含双极肌电信号，其中有双差分（DD）电极旨在抑制的串扰分量。因此，式（3）中的比值 $ \frac{G_{DDM}}{G_{SDM}} $ 可被定义为一个性能指标。由于简单差分模式（SDM）和双差分模式（DDM）均为同一数量级的肌电信号，该抑制系数无需达到共模抑制比（CMRR）那样高的水平。还应注意的是，与主要干扰分量位于工频及其谐波处的共模（CM）不同，简单差分模式（SDM）干扰具有肌电信号的频谱分布。

B. 有限输入阻抗

干电极带来特殊挑战，因为它们的阻抗幅值较高，且电极之间的阻抗变化不可预测。由于放大器输入具有有限的阻抗，这种变化会产生非零的共模到双差分模式增益，从而降低共模抑制比。该效应可被明确量化。

对于差分测量配置，通过如[13]所示的“分压效应”。但由于双差分放大器具有三个输入端，阻抗不平衡需要考虑两个自由度。图2的电路可用于分析不同情况下的这种效应。

对于电极阻抗不平衡，电极被赋予阻抗 $ Z_A $、$ Z_B $、$ Z_C $，且每个放大器输入被认为具有相同值的共模阻抗 $ Z_{in} $。然后，共模到双差分模式增益可表示为比值 $ \frac{V_{DDM}}{V_{CM}} $，由此得出
$$
\left| \frac{V_{DDM}}{V_{CM}} \right| \approx \frac{1}{2} \left| \frac{Z_A - Z_C}{Z_{in}} \right| + \frac{1}{2} \left| \frac{Z_A + Z_C - 2Z_B}{Z_{in}} \right|
\quad (4)
$$

当该值的幅值小于约10%时，可以得到此方程的良好近似解。

公式(4)表明不平衡的对称性很重要。如果第一项为0，但当 $ Z_A $ 和 $ Z_C $ 相对于 $ Z_B $ 不对称时，即 $ Z_A \neq Z_C $，第一项较大，而第二项通常可以忽略不计，因为它被除以 $ Z_{in} $。因此可得到 $ \left| \frac{V_{DDM}}{V_{CM}} \right| $ 的一个上限，并且可以进一步表示为最小抑制比。
$$
CMRR_{min}^{elec} \geq 20 \log_{10} \left( \frac{2Z_{in}}{|Z_A - Z_C|} \right)
\quad (5)
$$

当放大器的输入阻抗不平衡时，也会产生类似的效果。在这种情况下，可以将输入阻抗赋值为 $ Z_{inA} $、$ Z_{inB} $、$ Z_{inC} $ 和 $ Z_{in} $。假设电极阻抗相等，并再次考虑最坏情况。

当存在对称失衡时，由输入阻抗不平衡导致的抑制比结果
$$
CMRR_{min}^{amp} \geq 20 \log_{10} \left( \frac{2Z_{in}}{|\Delta Z_{in}|} \right)
\quad (6)
$$

III. 提出的电路

提出的电路如图3(a)所示。它能够以一种简单的方式测量双差分信号，仅使用一个四通道运算放大器集成电路；与使用三个仪表放大器相比，这种方法更简单且功耗更低。

差分输出结果
$$
V_{out+} = V_B - \frac{V_A + V_C}{2}, \quad V_{out-} = \frac{V_A + V_C}{2} - V_B
\quad (7)
$$

这会产生
$$
V_{out} = V_{out+} - V_{out-} = 2V_B - V_A - V_C
\quad (8)
$$

设计三个运算放大器用作缓冲器，以提供高输入阻抗。第四个运算放大器和无源网络实现双差分输出所需的求和与差分。

输出为低阻抗且为差分驱动输出，这非常方便，因为与现有的差分输入高分辨率Σ‐Δ ADC相匹配，并符合现代仪器仪表向全差分（FD）电路发展的趋势[21]–[23]。

全差分电路（FD circuits）比其单端（SE）counterparts具有更高的动态范围，从而更充分地利用可用的电源电压，这对于便携式、单电源、低压系统非常重要。像提出的电路（PROPOSED CIRCUIT）这样不与地连接的全差分电路，其共模抑制比（CMRR）理想情况下为无穷大，且不受元件失衡的影响[24]。然而必须指出的是，全差分电路需要两条独立的导线来传输输出信号，与单端电路相比，这要求从有源电极（active electrode）到主电路板增加一根额外的导线。

赋予阻抗的值可用于配置放大器的传递函数。如果给定纯电阻值 $ R_1 $、$ R_2 $，则输出结果为 $ V_{out} = \left( \frac{R_2}{R_1} \right)(2V_B - V_A - V_C) $。可以为图3(a)电路中的阻抗进行配置，以在前端提供增益和带宽限制，从而得到图3(b)所示电路。该电路具有以下带通传递函数：
$$
H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{G_0 s}{(s + \omega_L)(s + \omega_H)}
\quad (9)
$$

其中，中频增益为 $ G_0 $，下截止频率 $ \omega_L $ 和上截止频率 $ \omega_H $。

B. 干扰抑制

肌电图测量可接受的共模抑制比范围为100–120 dB [2]。驱动右腿电路通常能提供至少30–40 dB的共模干扰衰减，从而有效提高共模抑制比相应的量值[25],[14]。因此，测量前端合理的抑制值范围为70–90 dB。

所提出的电极的共模抑制比可根据(3)式计算。从(8)式可直接获得 $ G_{DDM} $，通过向所有节点施加一个公共输入即可计算 $ G_{CM} $。忽略二阶效应，共模抑制比结果为
$$
CMRR \approx 20 \log_{10} \left( \frac{A_{ol}}{CMRR_{OA4}} \right)
\quad (10)
$$

其中 $ CMRR_{OA4} $ 和 $ A_{ol} $ 分别为图3(a)中运算放大器OA4的共模抑制比（CMRR）和开环增益。因此，为了满足70–90 dB的目标，应选择在这两个参数在感兴趣频率范围内均不低于80–100 dB的运算放大器。

导致共模抑制比下降的另一个原因是电路的有限输入阻抗，如第二节所述。所提出的设计为每个输入采用了运算放大器的缓冲配置，这是文献[2],[26]中公认的一种解决方案，可利用低成本单片元件实现非常高的输入阻抗。

采用该方法所能提供的共模抑制比通过公式(5)确定。

根据以下考虑，在50赫兹下选择了方程变量的一系列取值：

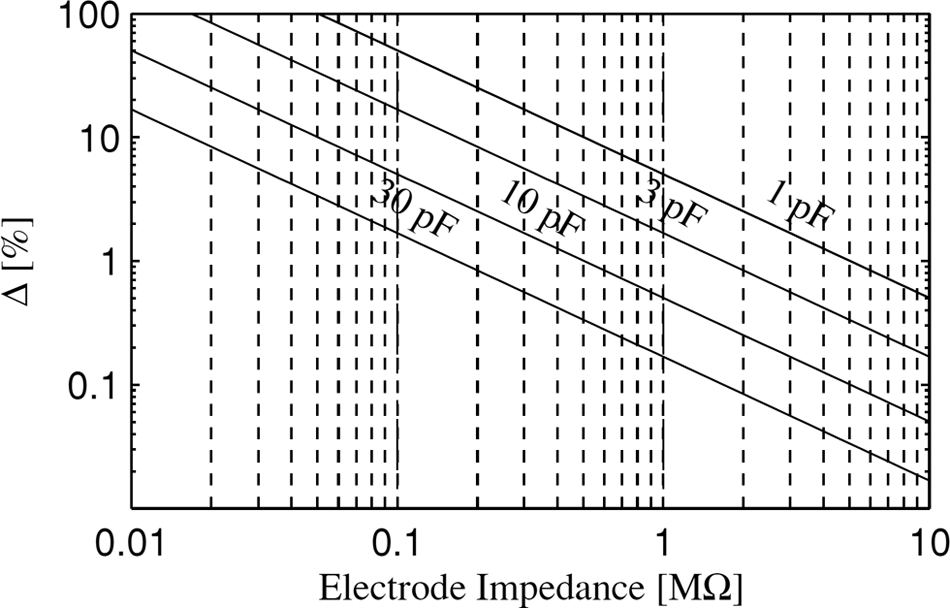
现有的运算放大器和仪表放大器的输入阻抗主要取决于其输入电容，因此 $ Z_{in} \approx \frac{1}{j\omega C_{in}} $。通常输入电容的取值范围为2 pF至30 pF（印刷电路板上的杂散电容也可能贡献几pF量级的值）。

在[12]中表明，不同类型的干电极当首次应用于未经处理的皮肤时，在50赫兹下的阻抗值可能高达 $ 100\,\text{k}\Omega $，并且在不同受试者或不同位置之间的变化可能高达100%。

使用这些值，以放大器的输入电容为参数，在图4中绘制了90 dB抑制水平的等高线。曲线的横轴为 $ Z_B $，纵轴为 $ Z_A $ 和 $ Z_C $ 相对于 $ Z_B $ 的百分比。例如，对于一个 $ 100\,\text{k}\Omega $ 阻抗，即使使用性能最好的运算放大器，若对称失衡超过10%，也会导致过大的干扰。

这些是非常不利的条件，但在接触板面积较小且刚刚放置到位，或皮肤非常干燥时可能会发生。这些极端情况可以通过轻微的皮肤准备来缓解，例如用自来水擦拭皮肤，或等待几分钟让汗液湿润电极下方区域[27]。

输入阻抗本身可能不平衡，从而引起不希望的模式转换。在传统的三仪表放大器差分驱动电路中，节点在两个仪表放大器输入端之间共享，因此它所呈现的阻抗是节点 $ V_A $ 和 $ V_C $ 阻抗的一半。这意味着对于（6），和
$$
Z_{inB} = \frac{Z_{inA} | Z_{inC}}{2}
\quad (11)
$$

因此，在这种情况下，共模抑制比始终取决于电极阻抗的平均值，而非其不平衡程度。对于一个相当低的3 pF输入电容，即可实现60 dB的抑制能力。所提出的电极改善了这一情况，因为每个输入节点都经过缓冲，各个缓冲器的输入阻抗变化可以忽略不计。

如前所述，简单差分模式存在不希望的串扰分量，由于电路不平衡，这些串扰分量可能会传递到双差分模式。从（7）式可以计算出从串扰分量模式到差分驱动模式的增益，理想情况下为0。考虑偏差

根据这些为方便起见用参数表示的值，这些阻抗可写为 $ R_1(1+\delta) $ 和 $ R_2(1+\epsilon) $，因此
$$
G_{SDM} \approx \frac{\delta - \epsilon}{2}
\quad (12)
$$

对于该情况可以近似为
$$
\left| \frac{G_{DDM}}{G_{SDM}} \right| \approx \frac{2}{|\delta - \epsilon|}
\quad (13)
$$

公式(13)采用抑制比系数的形式。当 $ R_1 $ 和 $ R_2 $ 按图3(b)实现时，电容器的阻抗在低频下占主导地位，其中 $ \delta $ 和 $ \epsilon $ 是电容器的容差。

该分析可应用于[8]中为分支电极建立的方程，以确定其输出作为双差分放大器信号模式的函数。

该方程表明，分支电极确实产生了所需的信号，但伴随有干扰，该干扰可能过高，因为它取决于电极阻抗的不平衡程度。

IV. 电极实现和辅助电路

A. 实现细节

采用提出的电路来构建肌电信号有源电极。所需四运放使用德州仪器的OPA4243实现。选择该器件的原因在于其具有低输入电容（2 pF）、高共模抑制比（104 dB @ 50赫兹）、相对较低的噪声（在10–500赫兹范围内）以及5V单电源工作特性。

组装了两个版本：1）增益为1的版本，将图3(a)中的所有阻抗设置为电阻器；2）带宽限制版本，如图3(b)所示，其3 dB带宽为16赫兹至500赫兹（根据[28]，适用于表面肌电信号），中频增益为10，通过以下元件值实现：$ R_1 = 100\,\text{k}\Omega $, $ R_2 = 1\,\text{M}\Omega $, $ C_1 = 100\,\text{nF} $, $ C_2 = 3.3\,\text{nF} $。

电极触点采用标准针式排针连接器实现。这些连接器为10毫米长的镀金棒，具有边长为0.64毫米的方形横截面积。

这些镀金棒平行放置，在单面印刷电路板背面相距10毫米，该印刷电路板用于承载电路。此电极间距在[29]中被证实对串扰抑制最为理想。

为了确保良好的接触，额外的机械支撑被用来将杆件与较宽的印刷电路板分离开。

电路的实现。四根导线提供电源和差分输出 通道。为测试目的，额外增加了导线以获取每个缓冲器的信号)

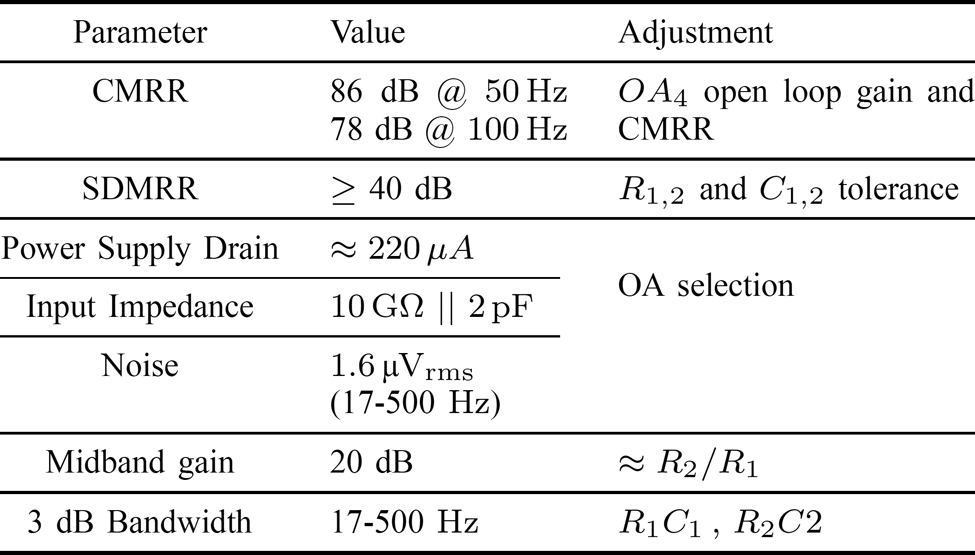
表I 典型性能特征和调整参数

标准排线电缆用作导联。完整的有源电极在没有外壳的情况下的尺寸为 $ 25 \times 10 \times 5\,\text{mm}^3 $。该设备的图片如图5所示。

在OA1和OA3的输出端额外焊接了两根导线，结合来自OA2的输出引线，可单独获取每个触点杆的信号。此项修改用于测试目的，以便除双差分驱动输出外，还能获得任意一对触点之间的双极信号。

所实现电极的工作参数已测量，并在表I中列出。这些参数符合文献[2],[22],[28]中推荐的参数，且可根据表I第三列所示的具体需求进行调整。

B. 辅助电路

采用了一款基于德州仪器ADS1298的先前开发的USB生物电势采集设备来对电极输出进行数字化。该前端每个采集通道均配有差分可编程放大器和24位 Sigma‐Delta转换器。

该系统包含一个驱动右腿电路[25]，用于设置2.5伏特的直流共模电压[30]，并使共模电源线干扰衰减30 dB。该驱动右腿电路具有独立的测量和反馈电极，配备直径为10 mm的按扣连接器，可用作干接触板或连接一次性电极。

为了将提出的电路与一种成熟的替代方案进行比较，使用图1(a)中的三运放仪表放大器拓扑构建了第二个电极。选用了模拟器件公司的AD623仪表放大器，因其具有2皮法的低输入电容和单电源供电特性操作。如有需要，两个电极可以在采集系统上同时工作，设置1.75 V参考电压，以为AD623提供工作范围。所有仪表放大器均配置为增益1。

五、实验测量

A. 验证三运放仪表放大器拓扑

所提出的电极与之前描述的3个仪表放大器差分驱动电极进行了对比测试。两个电路均焊接在相同的接触杆上，并使用测量系统的两个通道同时采集输出。本测试中使用了所提出电极的单位增益版本，以避免传输特性因元件容差而产生差异。

该“双通道”电极放置于其中一位作者前臂内侧隆起处，并使用可调节弹性带固定。驱动右腿电路（DRL）采用标准3M一次性电极贴附于手腕掌侧。执行食指的完全屈曲动作。信号以2000赫兹采样率、增益为1进行采集，并通过截止频率为10赫兹至600赫兹的二阶带通巴特沃斯滤波器进行离线滤波。

在肌肉激活期间，对4秒时间段内的两个信号进行了归一化互相关计算，得到相关系数。图6展示了表面肌电信号活动起始阶段的一段片段，用于视觉验证。该测试证实了所提出的电极产生的双差分驱动输出与现有替代方案相同。

B. 肌电图测量

接下来，将所提出的电极的带宽限制版本贴附在肱二头肌上，并进行等长收缩，尝试达到最大收缩。所得原始信号如图7(a)所示。第二次测量将电极放置在前臂内侧隆起处。选择该位置是因为通过轻柔的食指屈曲引发的肌肉活动可以轻松检测到，如图7(b)所示。这些样本记录可用于观察有无肌电活动时的信号水平，以及电极对高幅值和低幅值信号的测量性能。

显示了肱二头肌两次 连续强烈等长收缩的测量结果。(b) 当执行轻柔的食指屈曲时，从前臂内 侧隆起处获得的信号样本)

C. 串扰抑制

为了简单直观地展示所提出的电极的串扰抑制能力，在图8中展示了一组测量结果。选择了两个位置，通过特定动作激活空间上接近但足够分离的肌肉。利用原型电极的额外导线，同时获取电极的差分驱动输出和双极信号，其中双极信号是通过距离为10 mm的接触杆B和C的电位差获得的。所有信号均经过100 ms移动平均滤波器进行后处理。

对于图8(a)，电极放置在前臂的手指伸肌上，靠近肘部。选择食指伸展时产生最大振幅的位置。所观察到的信号由食指伸展、随后放松，然后小指伸展产生。对于图8(b)，电极放置在脸颊上，以检测颧肌的收缩。所观察到的肌电活动由以下动作诱发先做出微笑表情，然后咬紧下巴。两幅图均显示了与双差分电极中由两个杆构成的间距为10 mm的双极电极相比，双差分电极对非正下方肌肉产生的表面肌电信号的衰减效果。

在 前臂测量，依次伸展食指和小指；(b) 在脸颊测量，依次微笑和咬紧下巴)

D. 干扰抑制

在（11）中提出的结果已通过实验验证。本测试采用了图2的测量设置，在 $ V_{CM} $ 处施加了一个70赫兹的正弦波，并对两种电极进行了三组测量。在每次测量中，$ Z_A $、$ Z_B $ 和 $ Z_C $ 均使用三个阻值相同的电阻实现，且该阻值在各组测量之间变化。

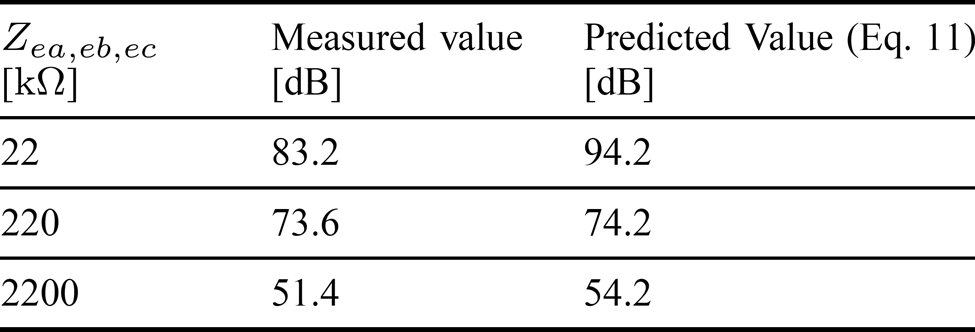
所提出的电极的共模抑制比为81分贝，在各次测量中未表现出显著变化。三运放仪表放大器拓扑结构的结果见表II。

对于最小的阻值，由于AD623的共模抑制比较低，该效应不明显；但当采用较高电阻值时，共模抑制比下降至接近（11）式预测的数值。

接下来，通过人体测量对该效应进行了测试。图2和表II显示，当电极阻抗非常高时，分压效应（与 $ Z_{source}/Z_{in} $ 成正比）以及输入阻抗不平衡（与 $ \Delta Z_{in}/Z_{in} $ 成正比）

表II 三种仪表放大器电极在源阻抗递增情况下的70赫兹共模抑制比

对于3个仪表放大器电极而言，可能会成为主要的共模干扰机制。因此，所提出的电极与3个仪表放大器电极相比，共模干扰将更低或相等，因为该关系与 $ (Z_{source}/Z_{in})/(Z_{source}/Z_{inB}) $ 之比成正比，且该比值最多为1。

为了避免其他干扰机制掩盖待观察的现象，将一个70赫兹的共模信号施加于人体，并通过所提出电极的一条引线进行测量。所提出的电极和3个仪表放大器电极并排放置在前臂上，并在不同条件下进行了5次记录：弹性带松紧不同、位置互换，以及应用时间从10秒到60秒不等。

对每次记录中存在的70赫兹信号进行了最小二乘逼近，并计算了抑制差异。在各项测量中，所提出的电极相比3个仪表放大器电极具有更好的抑制效果。

VI. 结论

文献支持使用双差分表面肌电电极来实现串扰抑制。特别是独立式干性有源电极具有多种应用，且已有商用设备存在。然而，关于所需放大器的设计细节和通用知识在文献中似乎较为缺乏。

因此，本文首先对三输入双差分放大器进行基本分析，以评估其工作参数。然后，提出了一种新型的双差分有源电极电路，该电路具有极低的复杂度和成本，仅包含一个四运放和少量无源器件，能够利用干触点采集表面肌电信号并抑制干扰源。

A. 电路分析

提出了表征放大器输入的三种信号模式：携带目标信号的模式、反映电磁干扰的模式，以及第三种正交模式，该模式值得注意，因为它就是双极肌电信号。由于双差分放大器的目的是衰减双极肌电中的串扰分量，因此必须抑制该信号，这意味着应关注使该信号到达输出端的电路参数。

接下来，得到了用于解释由电极和输入阻抗不平衡产生的电磁干扰的方程。由于存在三个端子，阻抗不平衡具有两个自由度，当节点以及阻抗（无论是电极还是输入端的阻抗）处于最不利情况时，将产生最坏情况干扰。

关于该节点呈对称不平衡。针对此情况的近似方程可用于获得最小预期共模抑制比的表达式，其为输入和电极阻抗值及不平衡的函数。实验验证了不平衡输入级导致的共模抑制比下降。

B. 提出的有源电极实现

提出了一种双差分有源电极的电路设计。该电路比文献中基于仪表放大器的方案更为简单，减少了设计所需的运算放大器数量，同时实现了与电极阻抗无关的双差分输出，不同于分支电极结构。该电路具有差分输出，可匹配当前高性能生物电势前端的输入。

提出的电路实现被描述，完全由 readily available 的商用组件构建，易于复制。其工作参数通过实验测量，结果与文献中找到的规格一致。这些参数可根据不同应用进行调整，如表I所示。

输入级为每块接触板设计了单位增益缓冲器。通过最坏情况电磁干扰电极不平衡方程，研究了使用现成组件实现该级时的限制。结论表明，即使使用目前最佳的组件，在某些极端情况下仍需要轻微的皮肤准备或等待几分钟。如果要避免这种情况，则需要更复杂的输入级。然而，理论和实验均表明，与基于三个仪表放大器的拓扑结构（其中一个接触板连接两个输入端子）相比，所实现的输入级具有更好的共模抑制能力。但应注意，这并不意味着整体共模抑制比本质上更优，整体共模抑制比仍取决于元件的选择。

对已实现的装置进行了实验测试，结果表明，在标准生物电位测量设置中，这种简单的拓扑结构产生的双差分输出与基于仪表放大器的电极相同。在身体不同位置使用干电极进行了多种表面肌电信号测量，且未进行皮肤准备。获得的信号质量较高，无明显电磁干扰成分，并展示了电极的串扰抑制特性。