集合系列(二十二) -二叉树实现详解

一、介绍

在前面的文章中，我们对树这种数据结构做了一些基本介绍，今天我们继续来聊聊一种非常常用的动态查找树： 二叉查找树。

二叉查找树，英文全称：Binary Search Tree，简称：BST，它是计算机科学中最早投入实际使用的一种树形结构，特性如下：

• 若左子树不为空，则左子树上所有结点的值均小于它的根结点的值；
• 若右子树不为空，则右子树上所有结点的值均大于或等于它的根结点的值；
• 它的左、右子树也分别为二叉查找树；

特性定义比较粗放，所以在树形形态结构上，有着多样，例如下图：

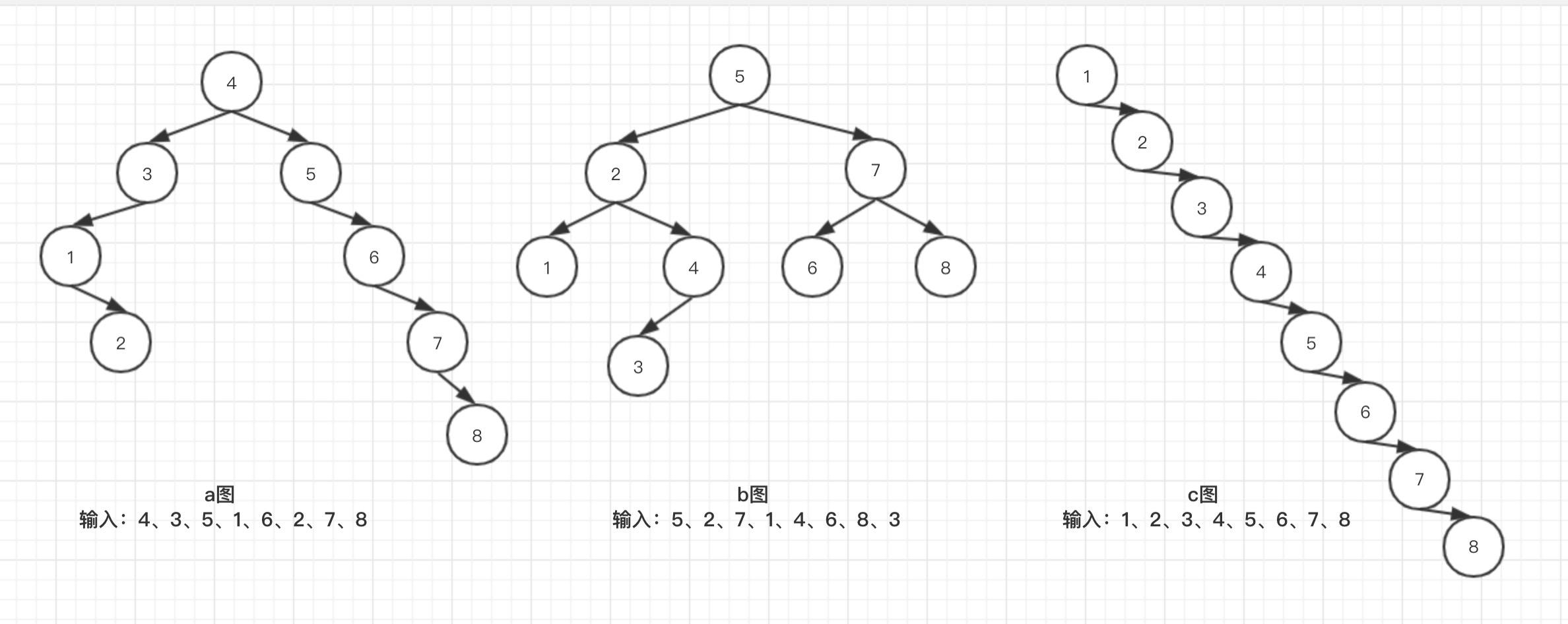
上图 a、b、c 三个图，都满足以上特性，也被称为二叉查找树，虽然通过中序遍历可以得到一个有效的数组：[1、2、3、4、5、6、7、8]，但是就查找效率来说，有着一定的差别，例如查询目标为8的内容，从根目录开始查询，结构如下：

• a图，需要5次；
• b图，需要3次；
• c图，需要8次；

由此可见，不同的形状，所需查找的次数是不一样的，关于这一点，后面我们在介绍平衡二叉查找树、红黑树这种数据结构的时候，会进行详细介绍。

虽然二叉查找树，在不同的形状下，查找效率不一样，但是它是学习其他树形结构的基础，了解了二叉查找树的算法，相信再了解其他二叉树结构会轻松很多。

二、算法思路

2.1、 新增

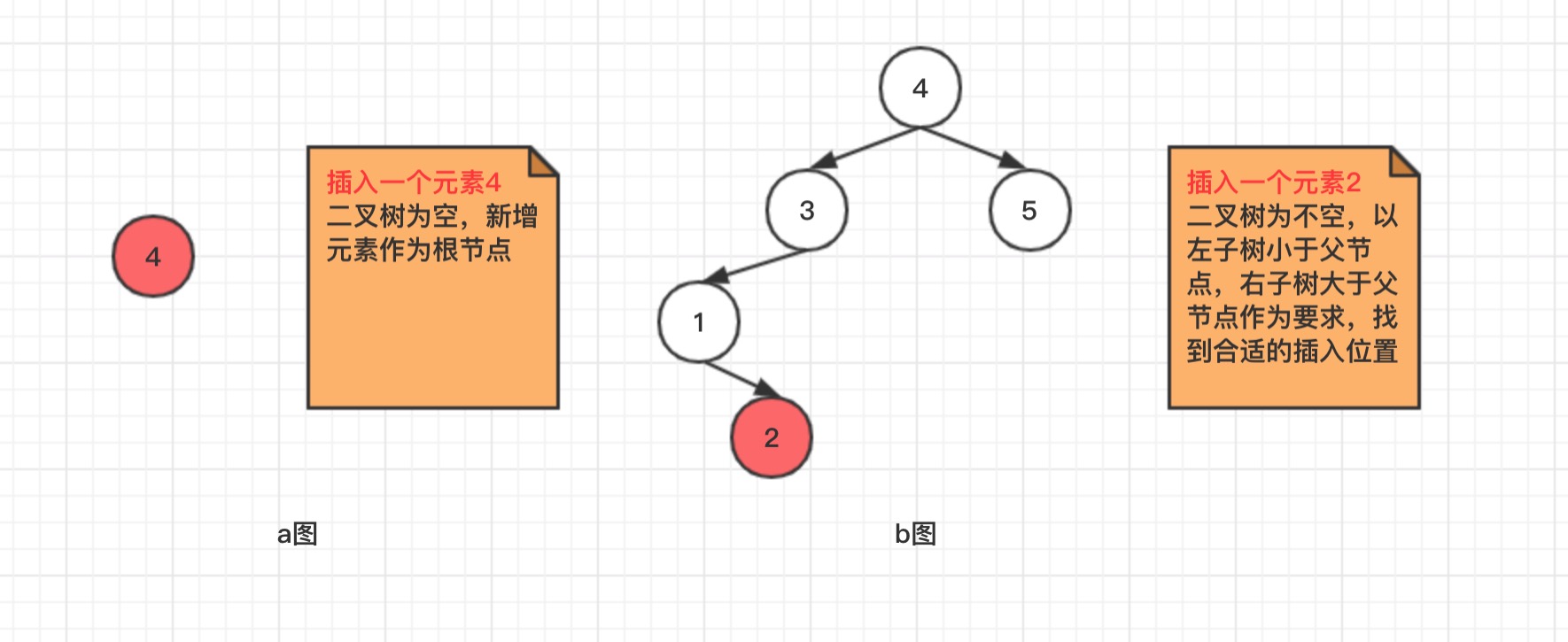
新增元素表示向二叉树中添加元素，比较简单。如果二叉树为空，默认第一个元素就是根节点，如果二叉树不为空，就以上面提到的特点为判断条件，进行左、右节点的添加。

2.3、 查找

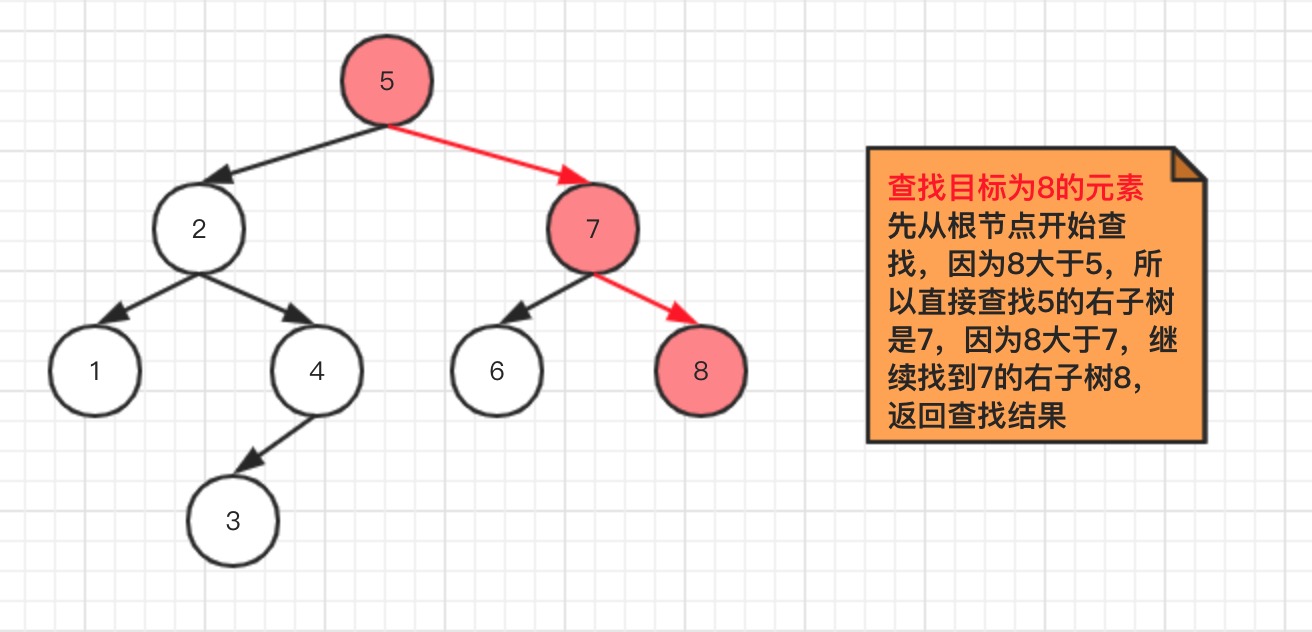
查找元素表示从根节点开始查找元素，如果根节点为空，就直接返回空值，如果不为空，通过以左子树小于父节点，右子树大于父节点的特性为依据进行判断，然后以递归方式进行查找元素，直到找到目标的元素为止。

2.2、 删除

删除元素表示从二叉树中移除要删除的元素，逻辑稍微复杂一些。同样，先要判断根节点是否为空，如果为空，直接返回，如果不为空，分情况考虑。

• 被删除的节点，右子树为空

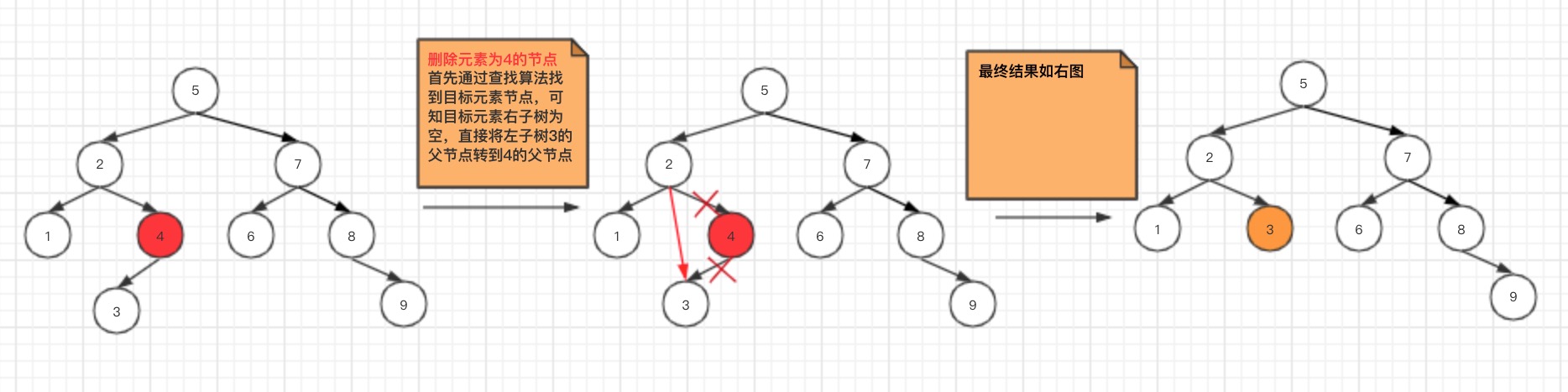
这种场景，只需要将被删除元素的左子树的父节点移动到被删除元素的父节点，然后将被删除元素移除即可。

• 被删除的节点，左子树为空

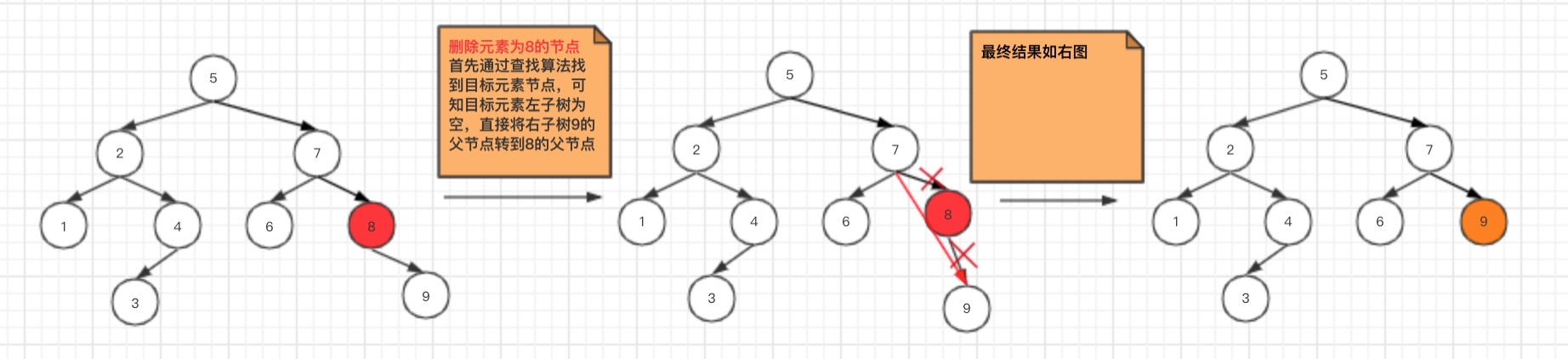
这种场景，与上面类似，只需要将被删除元素的右子树的父节点移动到被删除元素的父节点，然后将被删除元素移除即可。

• 被删除的节点，左、右子树不为空

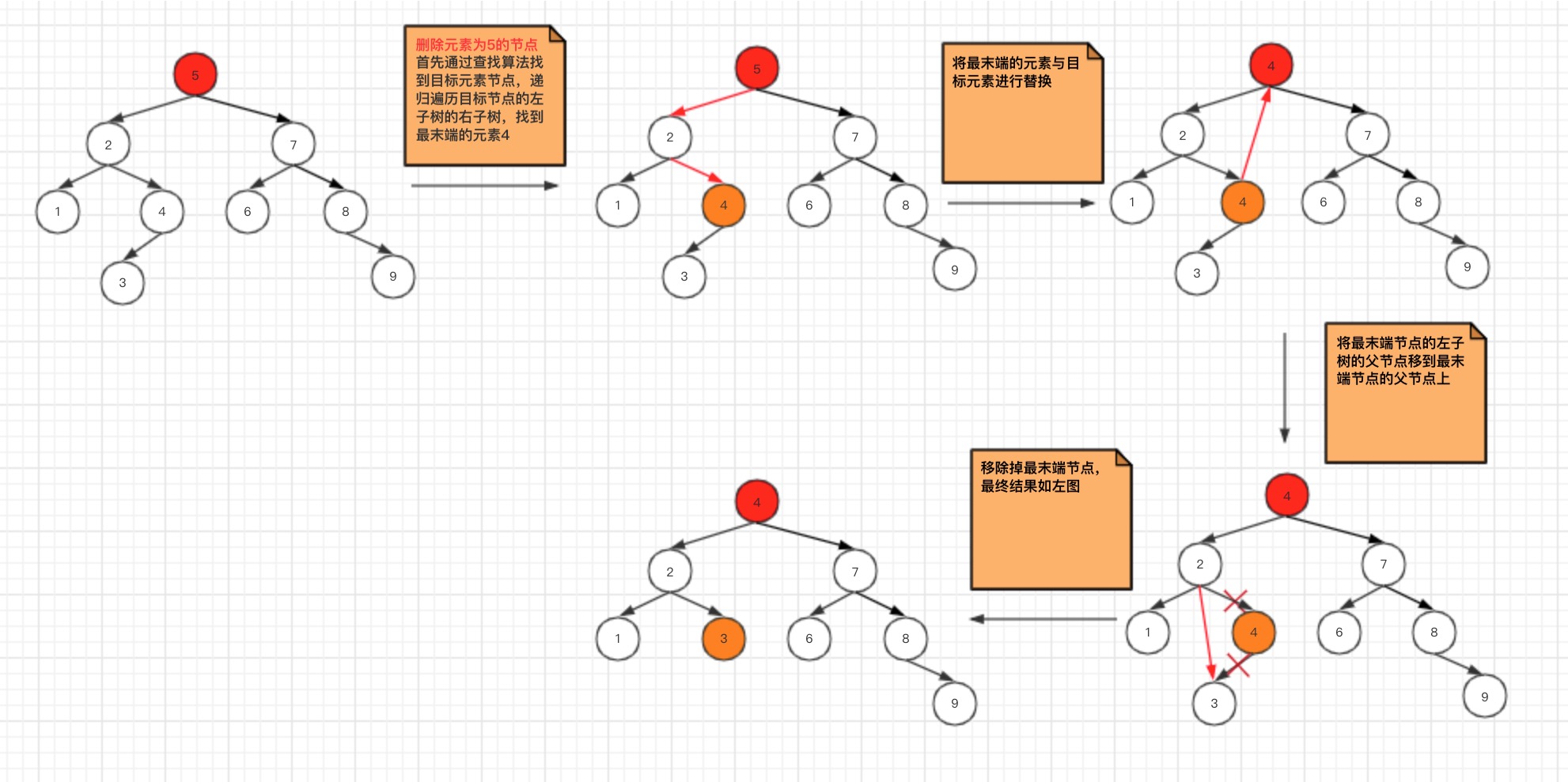
这种场景，稍微复杂一点，先定位到要删除的目标元素，根据左子节点内容一定小于当前节点内容特点，找到目标元素的左子树，通过递归遍历找到目标元素的左子树的右子树，找到最末端的元素之后，进行与目标元素进行替换，最后移除最末端元素。

2.4、 遍历

二叉树的遍历方式，分两类：

• 层次遍历，从根节点开始；
• 深度遍历，又分为前序、中序、后序遍历三种方式；

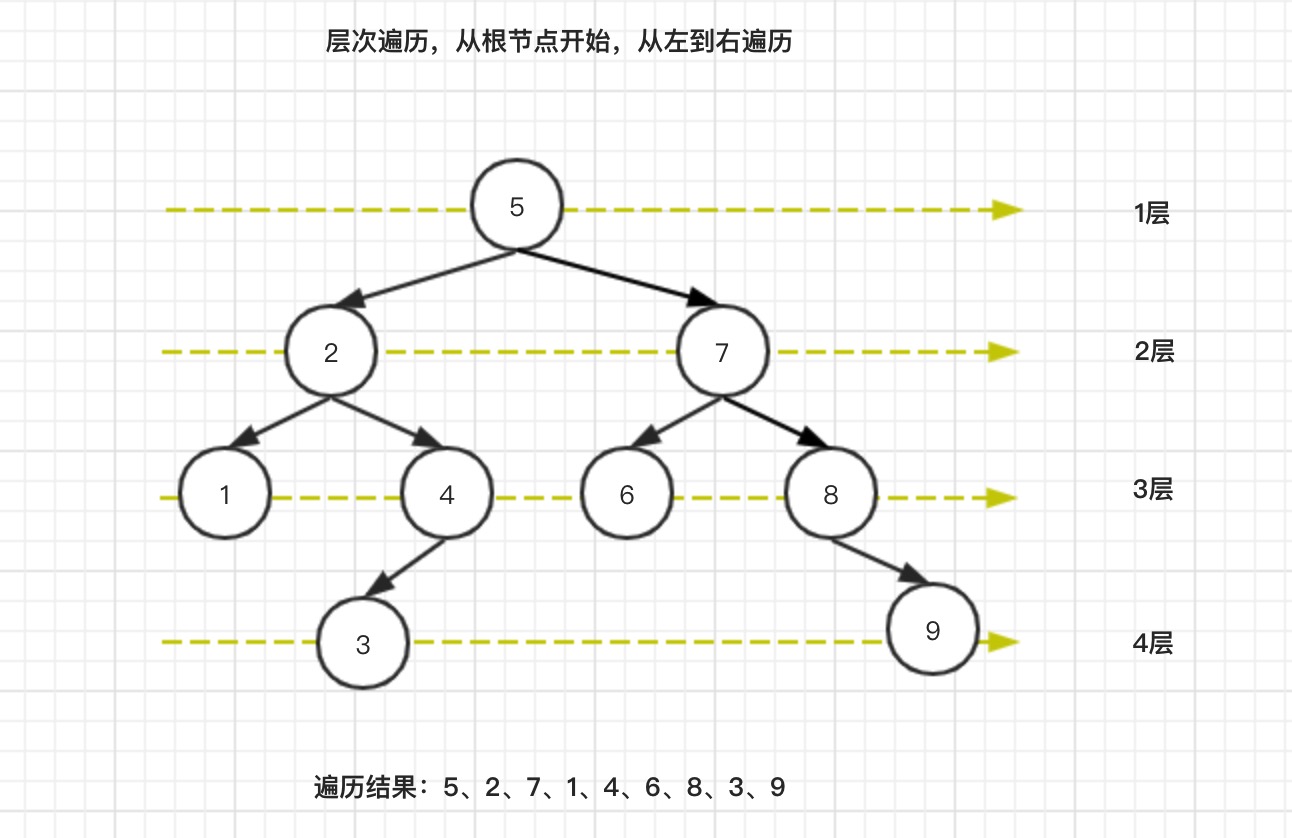
2.4.1、层次遍历

层次遍历，算法思路比较简单，从根节点开始，分层从左到右进行遍历元素。

2.4.2、深度遍历

深度遍历，在遍历起始位置上又分三种，分别是前序遍历、中序遍历、后序遍历，每种遍历方式输出的结果不一样。

• 前序遍历：从树根开始 -> 左子树 -> 右子树

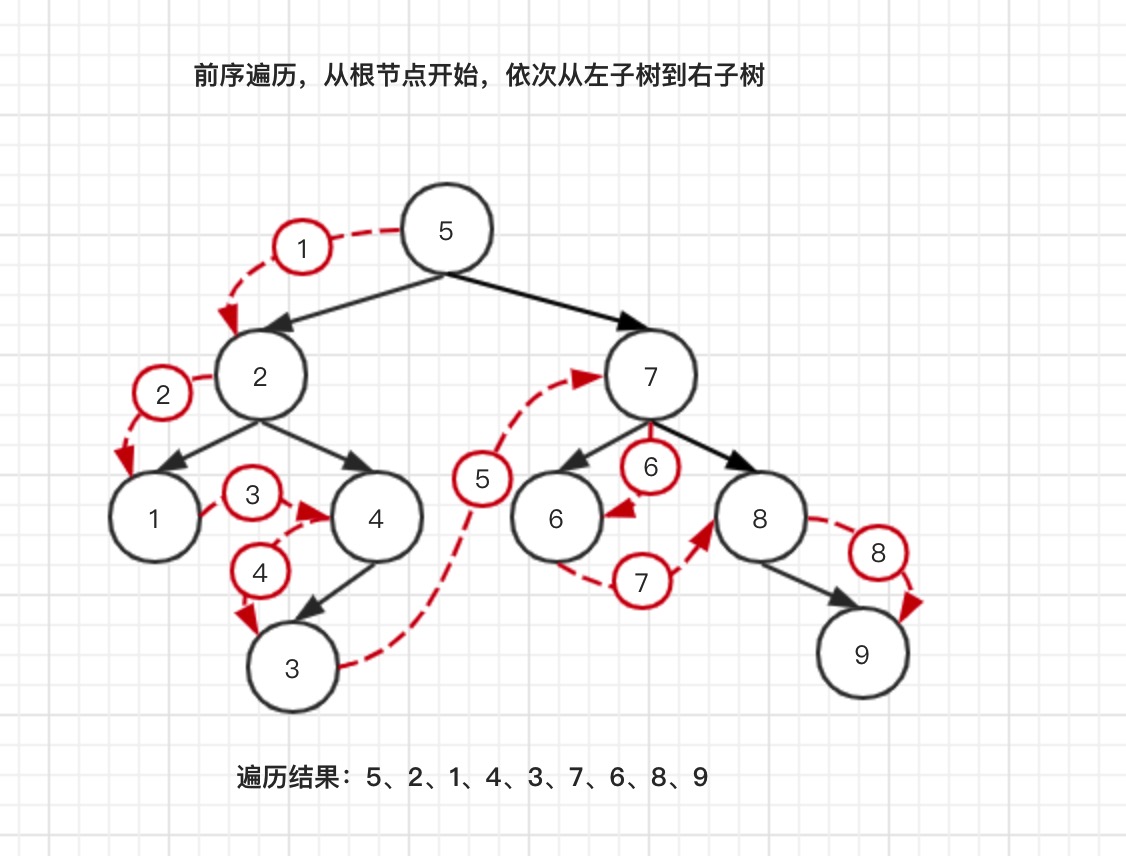
• 中序遍历：从最末端左子树开始 -> 树根 -> 右子树

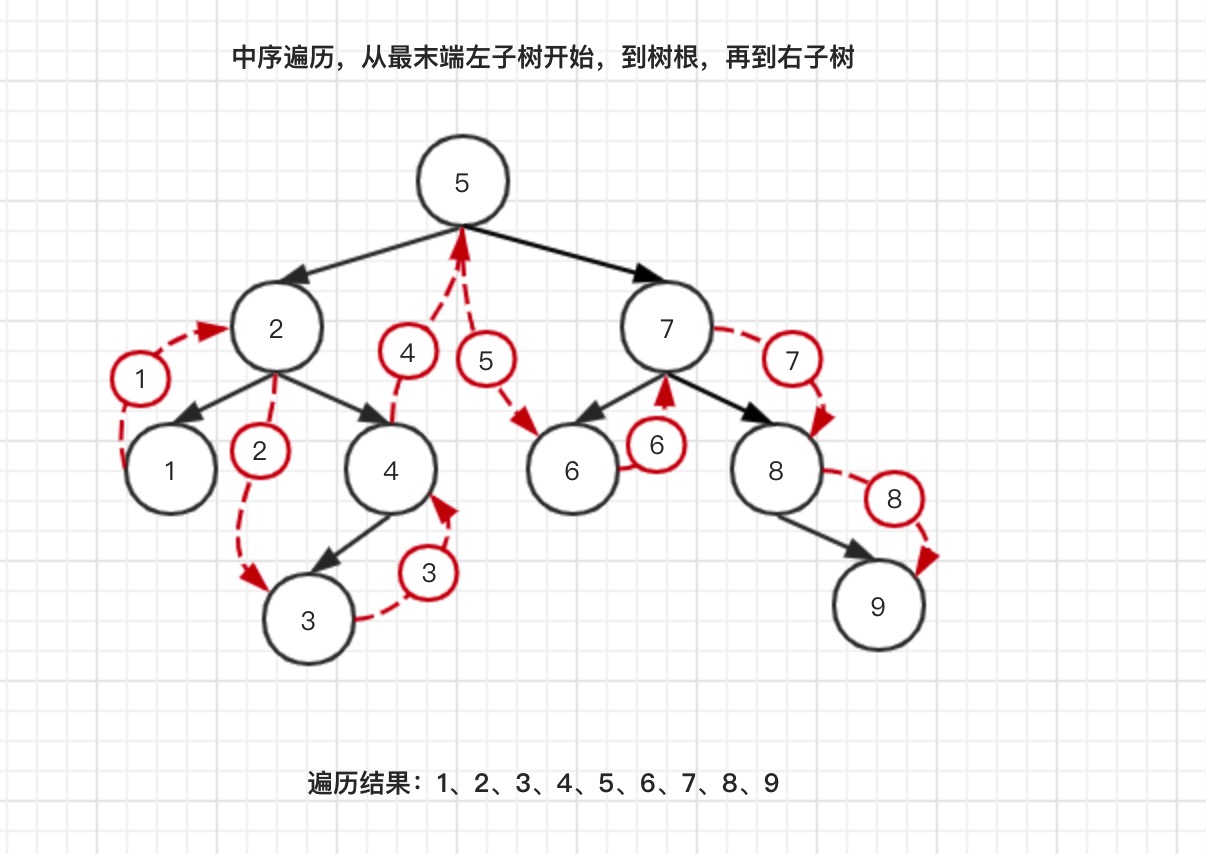
• 后序遍历：从最末端左子树 -> 右子树 -> 最后到树根

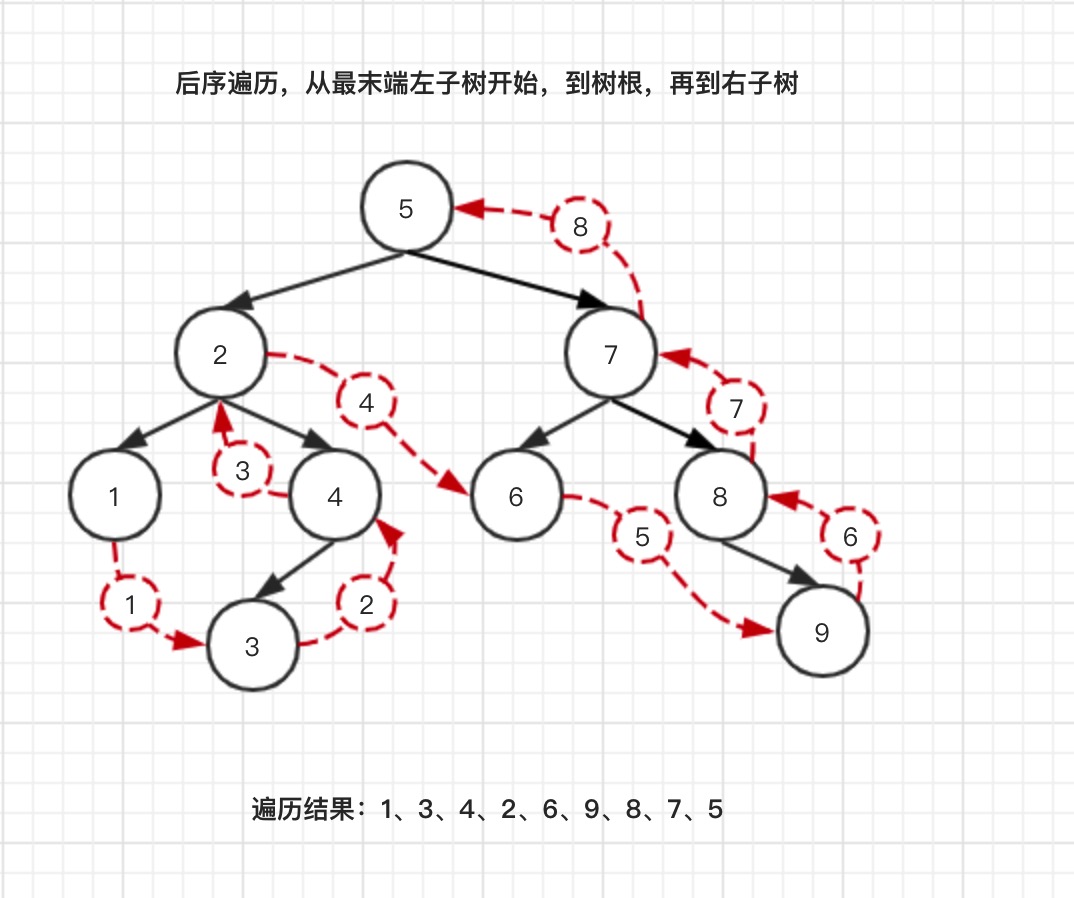
尽管二叉树在遍历方式上有多种，但是只要我们掌握了其中的思路原理，再去实现起来，就会轻松很多。

三、代码实践

首先创建一个实体数据结构BSTNode，内容如下：

/**
 * BST全称：Binary Search Tree
 * 二叉查找树，节点数据结构
 */
public class BSTNode<E extends Comparable<E>> {
   

    /**节点数据*/
    E key=null;
    /**直接父节点*/
    BSTNode<E> parent = null;
    /**当前节点的左子节点*/
    BSTNode<E> lChild = null;
    /**当前节点的右子节点*/
    BSTNode<E> rChild = null;

    /**构造方法*/
    BSTNode(E key){
   
        this.key = key;
    }
}

然后，创建一个二叉查找树操作类BinarySearchTree，内容如下：

/**
 * 二叉查找树 Binary Search Tree(BST)
 * 算法实现
 */
public class BinarySearchTree<E extends Comparable<E>> {
   

    /**定义根节点*/
    private BSTNode<E> root = null;

    /**
     * 获取二叉树根节点
     * @return
     */
    public BSTNode<E> getBoot(){
   
        return this.root;
    }

    /**
     * BST 查询关键字
     * 快速搜索
     * @param key
     * @return
     */
    public boolean search(E key){
   
        System.out.println("搜索关键字key=" + key + " ");
        if(key == null || root == null){
   
            return false;
        }else{
   
            System.out.print("搜索路径[");
            //从根节点开始查询
            if(searchBST(root,key) != null){
   
                //搜索到目标元素
                return true;
            }
            System.out.print("\n");
            return false;
        }

    }

    private BSTNode<E> searchBST(BSTNode<E> node, E key){
   
        if(node == null){
   
            System.out.print("],搜索失败"