集合系列(二十一) -树形结构介绍

一、前言

我们都知道，数组的特点是查询快，直接可以通过下标获取元素，时间复杂度为O(1)；但是当我们在指定的位置插入元素或者删除元素的时候，数组下标和所对应的元素是需要重新排列的，所需要的时间复杂度为O(n)！

所以对于频繁的插入、删除的场景，不建议采用有序数组！

可能有的朋友会想到，对于需要频繁的插入、删除的场景，可以使用链表结构，因为对于链表结构来说，在进行插入或者删除的时候，只需要改变元素的前驱或者后继节点的引用就可以了，所需要的时间复杂度为O(1)；但是如果我们想查询指定的内容时候，需要遍历链表元素并逐步判断，直到查找到目标元素为止，所需要的时间复杂度为O(n)！

所以对于查找频繁的数据，不建议使用链表！

哪有没有一种查询速度快、插入删除也很快的一种数据结构呢？

树就是其中一个！树这种数据结构，在计算机领域中有着很多的实际应用！比如说：

• mysql 数据库的索引就是 B+ 树结构，查找效率极高；
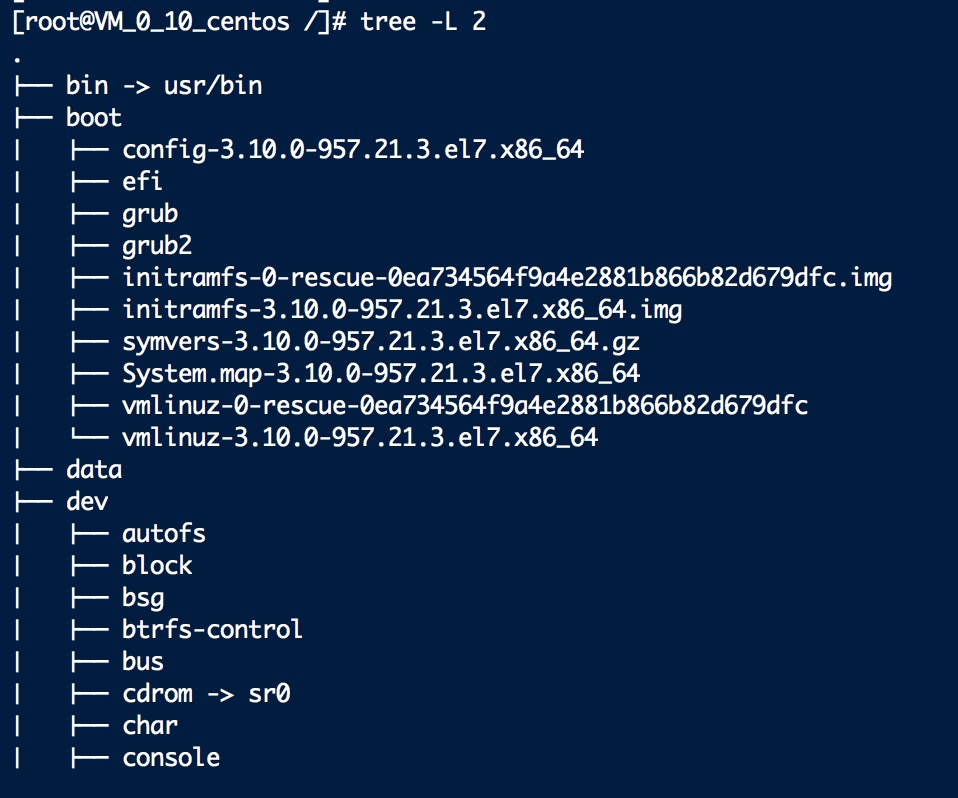
• Windows OS 的文件系统结构也是采用 B+ 树进行存储的；
• Linux 的文件系统结构同样也是采用 B+ 树进行存储的；

二、树介绍

说到树这种数据结构，相信很多人首先想到的就是二叉树！

不错，二叉树作为一个很重要的数据结构，在某些情况下既可以满足我们要求查询快的特点同时也可以满足插入删除也快的要求。

当然，在生活中我们可以看到树，其实是分很多种类的，我们刚刚也说了在某些情况下，假如一个树是任意自由的结构，那么它可能既达不到查询快也达不到插入删除快的要求，因此我们需要给树作出一些定义。

在现实中，树是一个根朝下、叶朝上的结构，而在计算机科学中，树是由n个有限节点组成一个具有层次关系的集合，看起来像一颗倒挂的树，根朝上、叶朝下，特点如下：

• 每个节点都只有有限个子节点或无子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；
• 树里面没有环路；

计算机科学中，树的定义：

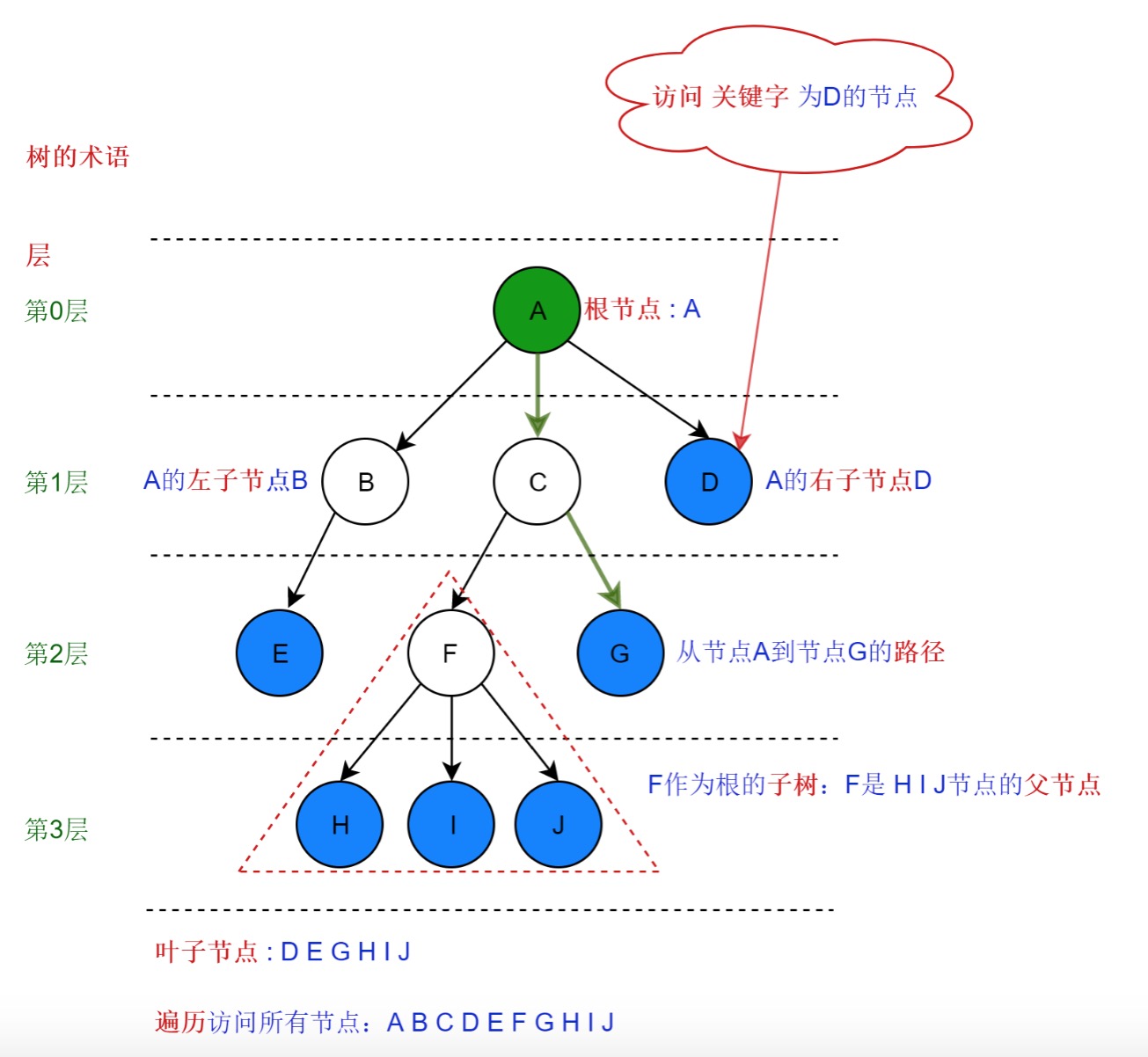
如下图，看起来像一颗树，但不是树结构：

虽然树做出了一些基本定义，但是不足以满足我们的需求，在计算机科学中，树可以被分为以下几种类型：

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；

对于无序树，也就是那种自由树结构，没有任何规律，所以无从查找，这种结构一般不考虑；而有序树，因为各个子节点存在一个的顺序关系，那么在查询的时候，就可以以此为基础进行查找！

当然，有序树又可以进行种类细分，内容如下：

• 二叉树：每个节点最多含有两个子树的树称为二叉树；
• B 树：一种平衡的多路查找（又称排序）树，能够保持数据有序，拥有多于两个子树；

上文说到的二叉树其实就是有序树的一种，在程序开发中，用的也是最多的一种树形结构！

而对于B 树，主要在文件系统和数据库领域中有所应用，像 Linux 操作系统的文件系统就是使用 B+ 树进行文件的存储。

三、二叉树

在计算机科学中，二叉树（英文名：Binary Tree）是每个结点最多有两个子树的树结构，通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

按照这个定义，在逻辑上二叉树可以进行五种基本形态的分类：

• 1