本文介绍了解决0-1背包问题的回溯法，并提供了详细的算法实现过程。通过对物品的选择与放弃，利用限界条件进行剪枝，提高了搜索效率。同时对比了优化前后的算法差异。
package com.duoduo.day316;
/**
* 回溯法
* 基础：选优搜索法(按照选优条件深度优先搜索，以达到目标）能进则进，进不了则换，换不了则退
* 0-1背包问题：
*
* 要素：1 定义问题的解空间----n个物品(X1...xn)
* 2 显约束 xi=0/1 i=1,2....n
* 3 约束条件-判断装入购物车的物品总重量是否超过购物车容量--确定可行解
* 4 限界条件--cp+rp > bextp---若价值上界<=当前搜索到的最优值 则无搜索必要
*
* @author 多多
*
*/
import java.util.Scanner;
public class Test5_2 {
static final int M=105;
static int n,W; //n表示n个物品，W表示购物车的容量
static int[] w=new int[M]; //w[i]表示第i个物品的重量
static int[] v=new int[M]; //v[i]表示第i个物品的价值
static int cw,cp,bestp;
static int[] x=new int[M]; //表示第i个物品是否放入购物车
static int[] bestx=new int[M]; //当前最优解
public static void main(String [] args) {
Scanner sc=new Scanner(System.in);
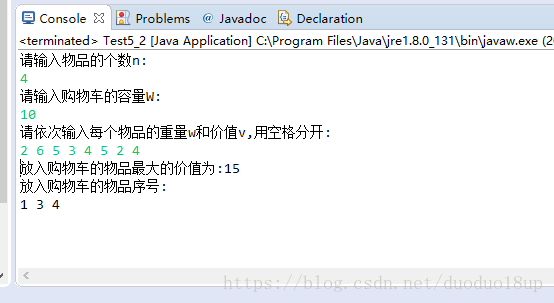
System.out.println("请输入物品的个数n:");
n=sc.nextInt();
System.out.println("请输入购物车的容量W:");
W=sc.nextInt();
System.out.println("请依次输入每个物品的重量w和价值v,用空格分开:");
for(int i=1;i<=n;i++) {
w[i]=sc.nextInt();
v[i]=sc.nextInt();
}
knapsack(W,n); //背包问题具体求解函数
sc.close();
}
public static void knapsack(int W, int n) {
//初始化
cw=0;
cp=0;
bestp=0;
int sumw=0; //用来统计所有物品的总重量
int sumv=0; //用来统计所有物品的总价值
for(int i=1;i<=n;i++) {
sumw+=w[i];
sumv+=v[i];
}
/*若所有物品总重量<= 购物车容量，直接输出最优解*/
if(sumw<=W) {
bestp=sumv;
System.out.println("放入购物车的物品最大价值为:"+bestp);
System.out.println("所有的物品均放入购物车");
return;
}
/*若所有物品总重量> 购物车容量，则需要使用搜索法 */
backtrack(1); //从第一层开始搜索
System.out.println("放入购物车的物品最大的价值为:"+bestp);
System.out.println("放入购物车的物品序号:");
for(int i=1;i<=n;i++) {
if(bestx[i]==1) //输出最优解
System.out.print(i+" ");
}
System.out.println();
}
/*用于搜索空间数 */
public static void backtrack(int t) { //t表示当前扩展节点在第t层
if(t>n) { //已经到达叶子节点
for(int j=1;j<=n;j++) {
bestx[j]=x[j]; //保存当前最优解
}
bestp=cp; //保存当前最优值
return;
}
if(cw+w[t]<=W) { //如果满足约束条件则搜索左子树
x[t]=1; //扩展左子树 标记为1 即放入物品t
cw+=w[t]; //对应的重量和价值均相应增加
cp+=v[t];
backtrack(t+1); //继续搜索t+1层
cw-=w[t]; //回溯则减去当初加上的重量和价值
cp-=v[t];
}
if(bound(t+1)>bestp) { //如果满足限界条件则搜索右子树
x[t]=0; //不放入物品 ，重量和价值均不改变
backtrack(t+1); //递推深度优先搜索第t+1层
}
}
/*计算上界（即剩余 物品的总价值）*/
public static int bound(int t) {
int rp=0; //剩余物品即第t~~n种物品
while(t<=n) {
rp+=v[t];
t++;
}
return cp+rp;
}
}
时间复杂度：O（1*2n+n*2n)=O（n*2的n次方） n为指数 约束条件O(1) 限界条件O(n)
空间复杂度 O(n) 辅助数组
优化算法：
package com.duoduo.day316;
/*物品类*/
public class Object {
int id; //物品序号
int d; //单位重量价值
}package com.duoduo.day316;
/**
* 回溯法
* 基础：选优搜索法(按照选优条件深度优先搜索，以达到目标）能进则进，进不了则换，换不了则退
* 0-1背包问题：
*
* 之前是： 当前价值cp+剩余物品总价值rp，有可能这些剩余物品容量>购物车容量
* 因而： 可以缩小上界 ，加快减枝速度 提高搜索速率
* 优化上界条件： 当前价值cp + 剩余容量可容纳的剩余物品的最大价值brp;
*
* @author 多多
*
*/
import com.duoduo.day316.Object;
import java.util.Scanner;
public class Test5_2_2 {
static final int M=105;
static int n,W;
static int[] w=new int[M]; //w[i]表示第i个物品的重量
static int[] v=new int[M]; //v[i]表示第i个物品的价值
static int cw,cp,bestp;
static int[] x=new int[M];
static int[] bestx=new int[M];
public static void main(String [] args) {
Scanner sc=new Scanner(System.in);
System.out.println("请输入物品的个数n:");
n=sc.nextInt();
System.out.println("请输入购物车的容量W:");
W=sc.nextInt();
System.out.println("请依次输入每个物品的重量w和价值v,用空格分开:");
for(int i=1;i<=n;i++) {
w[i]=sc.nextInt();
v[i]=sc.nextInt();
}
knapsack(W,n); //背包问题具体求解函数
sc.close();
}
public static void knapsack(int W, int n) {
//初始化
cw=0;
cp=0;
bestp=0;
int sumw=0;
int sumv=0;
Object[] Q=new Object[n]; //存放n个物品的数组
int []a=new int[n+1]; //辅助数组 用于把排序后的重量和价值传给-->原来的重量和价值数组
int[] b=new int[n+1];
for(int i=1;i<=n;i++) {
Q[i-1]=new Object(); //每一个数组元素都是一个Object对象
Q[i-1].id=i; //分别为每一个数组元素的属性赋值
Q[i-1].d=v[i]/w[i];
sumw+=w[i];
sumv+=v[i];
}
/*若所有物品总重量<= 购物车容量，直接输出最优解*/
if(sumw<=W) {
bestp=sumv;
System.out.println("放入购物车的物品最大价值为:"+bestp);
System.out.println("所有的物品均放入购物车");
return;
}
selectionSort(Q); //按单位重量价值进行排序
for(int i=1;i<=n;i++) { //把排序后的数据传递给辅助数组
a[i]=w[Q[i-1].id];
b[i]=v[Q[i-1].id];
}
for(int i=1;i<=n;i++) { //把排序后的数据传递给 原来的重量和价值数组
w[i]=a[i];
v[i]=b[i];
}
/*若所有物品总重量> 购物车容量，则需要使用搜索法 */
backtrack(1);
System.out.println("放入购物车的物品最大的价值为:"+bestp);
System.out.println("放入购物车的物品序号:");
for(int i=1;i<=n;i++) {
if(bestx[i]==1)
System.out.print(Q[i-1].id+" "); //输出最优解
}
System.out.println();
}
/*用于搜索空间数 */
public static void backtrack(int t) { //t表示当前扩展节点在第t层
if(t>n) { //已经到达叶子节点
for(int j=1;j<=n;j++) {
bestx[j]=x[j]; //保存当前最优解
}
bestp=cp; //保存当前最优值
return;
}
if(cw+w[t]<=W) { //如果满足约束条件则搜索左子树
x[t]=1; //扩展左子树 标记为1 即放入物品t
cw+=w[t]; //对应的重量和价值均相应增加
cp+=v[t];
backtrack(t+1); //继续搜索t+1层
cw-=w[t]; //回溯则减去当初加上的重量和价值
cp-=v[t];
}
if(bound(t+1)>bestp) { //如果满足限界条件则搜索右子树
x[t]=0; //不放入物品 ，重量和价值均不改变
backtrack(t+1); //递推深度优先搜索第t+1层
}
}
/*计算上界（即剩余 物品装满剩余的背包容量时所能获得的最大价值）*/
public static int bound(int t) {
//剩余物品为t~~n种物品
int cleft=W-cw; //目前购物车剩余容量
int brp=0; //剩余物品装满剩余的背包容量时所能获得的最大价值
while( t<=n && w[t]< cleft) { //加快剪枝速度 设定条件
cleft-=w[t];
brp+=v[t];
t++;
}
if( t<=n) { //采用切割的方式装满背包，只是在求上界，求解时不允许切割
brp+=cleft*v[t]/w[t];
}
return cp+brp;
}
//选择排序 按照单位重量价值进行排序
private static void selectionSort(Object[] Q) {
Object temp=new Object();
for(int i=0;i< Q.length-1; i++) {
for(int j=i+1;j< Q.length; j++) {
if(Q[i].d<Q[j].d) { //按照单位重量价值进行排序
temp=Q[i]; //但是交换的时侯是整个对象进行交换
Q[i]=Q[j];
Q[j]=temp;
}
}
}
}
}
时间复杂度：O(nlogn)再加上排序函数的时间
空间复杂度：增加 Object[] 两个辅助数组 均为o(n)
扫一扫
657
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
