针对王洪志老师给的习题3中的习题,给出部分习题的简要的解答思路(主要是没时间写仔细的分析),有错误的地方欢迎指出。
1.设有n个物品,第i个物品的价值是vi、重量是wi, 假设物品可以任意分割,给定一个背包,其能容纳最大重量为C,求该背包能容纳物品的最大价值。要求写出伪代码并分析算法正确性和复杂性。
就是普通的分数背包问题,不解释。
2.有6种硬币,面值是1分, 2分, 5分, 1角,5角,1元,给定一个钱数n,求出一个硬币组合,要求面值总和为n且硬币个数最少,假设每种硬币个数无限。要求写出伪代码并分析算法正确性和时间复杂性。
贪心选择:在不超过总币值n的条件下先选择币值最大的硬币,证明可以通过替换法进行证明。
3.存放于磁带上文件需要顺序访问。故假设磁带上依次存储了n个长度分别是L[1],….,L[n]的文件,则访问第k个文件的代价为 。现给定n个文件的长度L[1],….,L[n],并假设每个文件被访问的概率相等,试设计一个算法输出这n个文件在磁带上的存储顺序使得平均访问代价最小。。答案要求包含以下内容:(1)证明问题具有贪心选择性;(2)证明问题具有优化子结构;(3)给出算法并分析算法的时间复杂度。
贪心选择:将文件长度最小的文件放在最前面
4.
设有n个正整数,将它们连接成一排,组成一个最大的多位整数。
例如:n=3时,3个整数13,312,343,连成的最大整数为34331213。
又如:n=4时,4个整数7,13,4,246,连成的最大整数为7424613。
输入是n个正整数,输出是这n个正整数连成的最大多位整数,要求用贪心法求解该问题。答案要求包含以下内容:(1)证明问题具有贪心选择性;(2)证明问题具有优化子结构;(3)写出算法伪代码并分析算法的时间复杂度。预处理:对所有的数据进行预处理,遍历所有的数据,找到位数最大的树,并将它的位数记为k;对所有位数小于k的树,通过在末尾加0的方式改造成k位的数据,例如:
原数据:7、13、4、246
预处理之后:700、130、400、246
贪心选择:在预处理的数据中,优先选择最大的数据作为合成整数的高位数据;在合成时使用与预处理数据对应的原数据进行合成
例如在上面所给的数据中,先选择700,再选择400,在选择246,最后选择130;合成后的整数位7424613
5.
设x1, x2, …., xn是实数轴上的n个点,若用单位长度的闭区间覆盖这些点,至少需要多少单位长度闭区间?
预处理:首先很明显应该将n个点进行一次排序。这样就可以从左向右依次计算。
贪心选择:只需要先将排好序的数组最左边元素加上区间长度,把覆盖后的这一段去掉,然后再求出剩余段的最左边元素,重复上述过程即可求得覆盖点集的最少区间数。
8.给定n个自然数d1, d2, …, dn, 设计算法,在多项式时间确定是否存在一个无向图G,使它的结点度数准确地就是d1, d2, …, dn, 要求G中在任意两个结点之间至多有一条边,且不存在一个结点到自身的边。
解决方法:首先对n个数据进行排序,然后选出当前最大的数据d,将其从数据中删除,从剩余的数据中由最小的非零数据开始选取d个数据,若剩余的数据中不足d个非零数据,则返回错误,即不存在图G;若剩余的数据中可以选择出d个非零的数据,则对这d个数据分别减一;循环下去,直到数据中的数据全部为0.
9.考虑一种特殊的0-1背包问题,有n个物品,每个物品价值和重量都相等,背包能容纳的最大重量是C, 回答下列问题:
若物品的重量(价值)分别是1, 2, …,2n, 证明该0-1背包问题可以用贪心法求解并写出该贪心法。
贪心选择:优先选择小于C的最重的物品放入背包
伪代码:
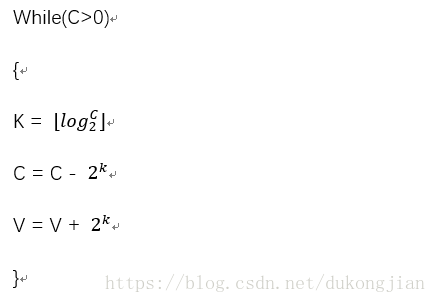





















 1026
1026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








