代码随想录算法训练营第二天/977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵2

目录

今日学习内容：

---

977.有序数组的平方

209.长度最小的子数组

59.螺旋矩阵2

---

977.有序数组的平方

题目链接：https://leetcode.cn/problems/squares-of-a-sorted-array/

题目描述：

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

1.想法：

这道题已经是二刷了，所以在看到这道题后的思路是按照原来在代码随想录里面的方法理解那样的。首先先关注到这道题目需要注意的问题：非递减数组，并且里面含有负数；求各数平方后得到按顺序排列的新数组。非递减的数组从小到大排序，但是里面有负数，负数平方后可能比一些正数要大，所以原数组里面的数据平方后是数组两边比较大，往中间逐渐递减，所以应该要从原数组两边开始遍历比较，然后将较大的平方后的数从后往前放入新数组里面，这样保证新数组也排好序；原数组是排序好的，所以可以使用双指针法进行；

2.实现过程注意：

从两边开始遍历比较，当将较大数平方放入新数组后，那么原本指向那个较小数的指针不用变，直到它所指数平方较大被放入新数组才进行改变；

3.代码实现过程：

class Solution {
    public int[] sortedSquares(int[] nums) {
       int left=0;
       int right=nums.length-1;
       int [] res=new int[nums.length];
       int index=res.length-1;

       while(left<=right){
           if(nums[left]*nums[left]>nums[right]*nums[right]){
               res[index]=nums[left]*nums[left];
               index--;
               left++;
           }else{
               res[index]=nums[right]*nums[right];
               index--;
               right--;
           }
       }
       return res;
    }
}

---

209.长度最小的子数组

题目链接：https://leetcode.cn/problems/minimum-size-subarray-sum/

题目描述：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

1.思考：

这道题目是二刷，第一次看的时候也完全没有头绪不知道该怎么做，在看了代码随想录文章跟着理解才明白这个过程，这里提出一个有趣的说法来描述了这个实现过程，把这个找到最小子数组的过程叫做“滑动窗口”；“滑动窗口”的意思是：这道题使用“双指针法”，左右指针将数组里面的部分数值包括在内,当子数组和过小时，左指针始终保持不变，右指针移动；而子数组总和过大时，左指针就要相应的右移了；然后这个过程不不断求出来符合要求的子数组，那么要每一次对这些子数组的长度进行判断，判断可以利用Math类来进行获取到最小的数组，所以在一开始可以先将长度设为最大的整数，还有一点需要注意的：数组是从0开始遍历的，所以计算子数组的长度时，千万要记得加1。

2.代码实现过程：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
       int left=0;
       int right;
       int sum=0;
       int result=Integer.MAX_VALUE;
       for(right=0;right<nums.length;right++){
           sum+=nums[right];
           while(sum>=target){
               result=Math.min(result,right-left+1);
               sum-=nums[left];
               left++;        
           }
       }
       return result==Integer.MAX_VALUE?0:result;
    }
}

---

59.螺旋矩阵2

题目链接：https://leetcode.cn/problems/spiral-matrix-ii/

题目描述：

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

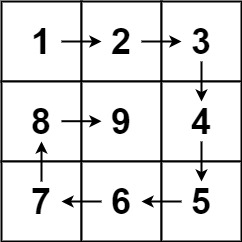
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]] 

1.第一想法：

这道题不算二刷，因为之前看的时候根本无法完全理解这个过程，知道要将数字从顺时针的方向来进行不断的循环填充，然后知道可能需要不断的循环，然后模拟四边的过程，知道该怎样的走向，但是完全不知道该如何去实现这个过程。

2.看代码随想录后：

这次花了很长时间总算能懂全部过程了包括模拟过程中量的变化，模拟过程非常重要的是四条边的走向从哪个位置开始又从哪个位置结束，那么这些问题的解答分别是：1.上边，从左往右，但是只到倒数第二个位置；2.右边，从上往下，也只是到倒数第二个位置；3.下边，从右往左，逐渐递减到倒数第二个位置，所以这里的判断条件需要注意；4.左边，从下往上，逐渐递减到倒数第二个位置。这个过程每条边都是以这条边的倒数第二个位置结束，因为最后一个都要作为下一条边的开始。

四条边的模拟结束后，这个时候要想到一个问题：奇数和偶数是否有分别呢？回答：是有分别的，动手分别画奇数和偶数的实现过程，就会发现当模拟到最后，对于偶数来说是已经完成了所有数的填充，但是对于奇数来说还剩下中间的一个数是没有填充的，所以需要多进行一个对奇数的判断，然后将这个数填充。

3.代码实现过程(与视频结合理解)：

class Solution {
    public int[][] generateMatrix(int n) {
       //实质是模拟四条边的过程
       //[i][j]:[行][列]

       int start=0;
       int [][] res=new int [n][n];
       int i,j;
       int loop=0;
       int count=1;
       
       //首先需要对需要循环次数做判断,每循环一次需要加1，这样才能判断还需要再循环几次
       while(loop++<n/2){
           //模拟上边，从左往右,行数不变，列数递增
           for(j=start;j<n-loop;j++){
               res[start][j]=count++;
           }

           //模拟右边，从上到下，列数不变，行数递增
           for(i=start;i<n-loop;i++){
               res[i][j]=count++;
           }

           //模拟下边，从右到左逐渐递减，行数不变，列数变，初始值也已经给出所以不用再写
           for(;j>=loop;j--){
               res[i][j]=count++;
           }

           //模拟左边，从下到上逐渐递减，行数变，列数不变，初始值和下边一样
           for(;i>=loop;i--){
               res[i][j]=count++;
           }
           //第n次循环时，起始位置是往右移了也就是减小了的
           start++;
       }

       //判断为奇数时情况
       if(n%2!=0){
           res[start][start]=count;
       }
       return res;

    }
}

---

总结：

1.这三题于我而言都是有一定难度的，特别是螺旋矩阵的模拟过程，对于起点终点判断，然后虽然理解了题目并且知道了实现过程但是也无法正确写出正确的代码，对里面一些量的变化反应不过来，所以之后对这道题需要多定期进行看视频结合的复习。

2.这两天完成的五道题是数组相关的内容，之后应该进行一次总的复习，将这些题涉及的内容再回顾一遍，特别是在数组中经常使用到的“双指针法”。