cmu秋季的ml课程 deep learning 的生物学基础 --1

1. 神经元结构
   

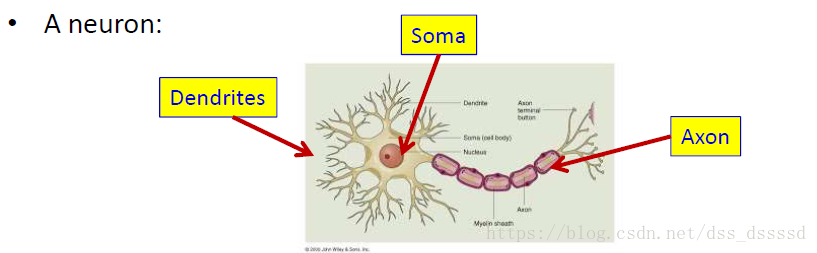
• 信号通过树突（dendrites）传入神经元胞体(soma)
• 信号通过轴突（axon）传递给其他的神经元 每个神经元只有一个轴突，成熟的神经元不经过细胞分裂

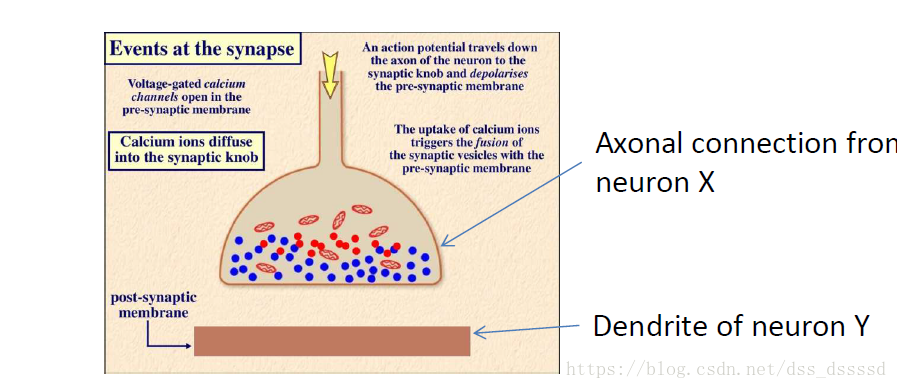
• 如果神经元A重复激励神经元B，那么他激励神经元B的能力会变得更强，在生物学上表现的就是A和B的突触旋钮会变得更大
• 用数学模型表示：
  $$w_i=w_i+\eta x_{i}y$$
  $w_i$是第$i$个输入神经元$x_i$对输出$y$的权重
• 这个简单的公式是许多机器学习算法得基础

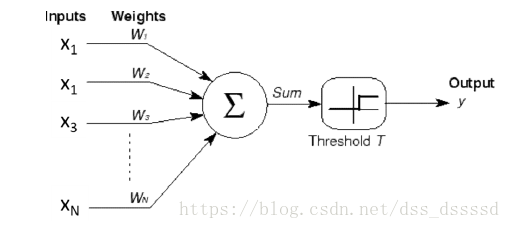
3. Rosenblatt’s perceptron
   

• 输入的线性组合

• 阈值逻辑： 如果输入线性组合之和超过阈值，输出为1
  $$f(n)=\{\begin{array}{ll}1,& \text{if ∑iwixi−T>0 }\\ 0,& \text{else}\end{array}$$

• 提供了学习算法
  $$\overrightarrow{W}=\overrightarrow{W}+\eta (d(\overrightarrow{x})-y(\overrightarrow{x}))\overrightarrow{x}$$

  • $d(x)$是神经元对于输入$x$的期望输出
  • $y(x)$是实际输出

优势：

• 可执行布尔任务（非， 或， 与）
• 能够自动更新权值
• 算法可收敛

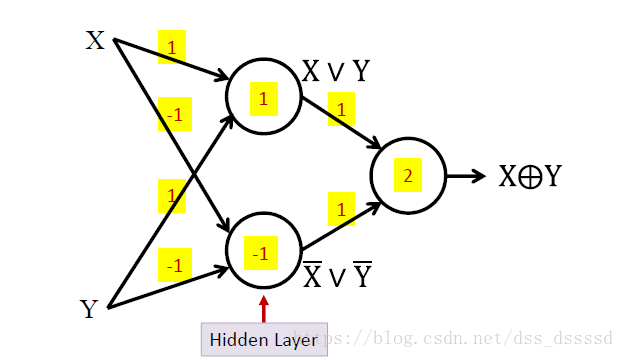
不能执行异或算法
说明仅有1个神经元完全不够，因而出现了多层感知机(MLP)

summary:

1.多层感知机是连接计算图（Multi-layer perceptrons are connectionist computational models）

2 .多层感知机可以用来分类（MLPs are classification engines）

3. 多层感知机也可以模拟输出为任意连续值的函数（MLP can also model continuous valued functions）

4. 人工智能就是通过网络构建可以模拟从输入到输出的函数（Interesting AI tasks are functions that can be modelled by the network）