1 概念介绍
1.1 Random Variable · 随机变量
- 一维随机变量
- 多维随机变量
1.2 Stochastic Process · 随机过程
随机过程研究的不再是单个的随机变量,而是一组随机变量,这一组随机变量之间有非常紧密的关系。
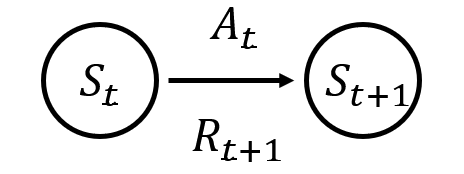
例:设今天的股票价格为St,则明天的股票价格St+1肯定与今天的价格有关系的,依次类推,后天的、大后天的……以及昨天的、前天的都与今天的St有关系,他们就可以归纳成一个随机过程:
{ S } t = 1 ∞ = … S t − 1 , S t , S t + 1 , … \{S\}_{t=1}^{\infty}=…S_{t-1},S_{t},S_{t+1},… {S}t=1∞=…St−1,St,St+1,…
1.3 Markov Chain/Process · 马尔可夫链/过程
马尔可夫过程是一种特殊的随机过程,具备马尔可夫性质的随机过程叫做马尔可夫过程。
- Markov Property · 马尔可夫性质
文字描述:当前的状态只和上一时刻有关,在上一时刻之前的任何状态都和我无关
数学描述: P ( S t + 1 ∣ S t , S t − 1 , S t − 2 , … , S 1 ) = P ( S t + 1 ∣ S t ) P(S_{t+1}|S_t,S_{t-1},S_{t-2},…,S_1)=P(S_{t+1}|S_t) P(St+1∣St,St−1,St−2,…,S1)=P(St+1∣St)
【拓展】
- 二阶马尔可夫性质: P ( S t + 1 ∣ S t , S t − 1 , S t − 2 , … , S 1 ) = P ( S t + 1 ∣ S t , S t − 1 ) P(S_{t+1}|S_t,S_{t-1},S_{t-2},…,S_1)=P(S_{t+1}|S_t,S_{t-1}) P(St+1∣St,St−1,St−2,…,S1)=P(St+1∣St,St−1)
- 三阶马尔可夫性质: P ( S t + 1 ∣ S t , S t − 1 , S t − 2 , … , S 1 ) = P ( S t + 1 ∣ S t , S t − 1 , S t − 2 ) P(S_{t+1}|S_t,S_{t-1},S_{t-2},…,S_1)=P(S_{t+1}|S_t,S_{t-1},S_{t-2}) P(St+1∣St,St−1,St−2,…,S1)=P(St+1∣St,St−1,St−2)
【理解】
- 在现实生活中,比如说一个人的游戏水平,跟昨天的游戏水平是最有关系的,跟十年前他的游戏水平关系就不大了。
- 马尔可夫性质存在的意义是为了简化计算。
1.4 State Space Model · 状态空间模型
State Space Model=Markov chain+Observation
状态空间模型=马尔可夫链+观测变量
1.5 Markov Reward Process · 马尔可夫奖励过程
Markov Reward Process=Markov chain+Reward
马尔可夫奖励过程=马尔可夫链+奖励
从一个状态转移到另一个状态,都会有一个奖励。
1.6 Markov Decision Process · 马尔可夫决策过程
Markov Decision Process=Markov chain+Reward+Action
马尔可夫奖励过程=马尔可夫链+奖励+行为
这里的“行为”是指可以影响到状态的行为,比如说股市里的政策制定者,通过某个行为,影响股票价格,同时得到一定的奖励。
通常同花体表示某个集合:
- S \mathcal{S} S:state set · 状态集 → S t \rightarrow S_t →St
-
A
\mathcal{A}
A:action set · 行为集,有时候表示为
∀
s
∈
S
,
A
(
s
)
→
A
t
\forall s\in\mathcal{S},\mathcal{A}(s)\rightarrow A_t
∀s∈S,A(s)→At
因为任何一个行为都是都是在某种状态下做出的,所以有了上面的表示方法。 -
R
\mathcal{R}
R:reward set · 奖励集
→
R
t
+
1
\rightarrow R_{t+1}
→Rt+1
在t时刻的做出的行为一般在t+1时刻才能得到奖励,故一般 S t , A t S_t,A_t St,At与 R t + 1 R_{t+1} Rt+1对应
2 动态特性
【回顾】
Markov chain: S \mathcal{S} S
MRP: S , R \mathcal{S},\mathcal{R} S,R
MDP: S , R , A ( s ) \mathcal{S},\mathcal{R},\mathcal{A}(s) S,R,A(s)
2.1 状态转移矩阵
只能针对状态空间是离散的情况,描述马尔可夫链的动态特性,表示从一个状态转移到另一个状态的概率
【例】
一个马尔可夫链有10个随机变量 S t ∈ { S ( 1 ) , S ( 2 ) , … , S ( 9 ) , S ( 10 ) } S_t\in\{S^{(1)},S^{(2)},…,S^{(9)},S^{(10)}\} St∈{S(1),S(2),…,S(9),S(10)}
其状态转移矩阵为:
S ( 1 ) S ( 2 ) ⋯ S ( 9 ) S ( 10 ) S ( 1 ) p 11 p 12 ⋯ p 19 p 110 S ( 2 ) p 21 p 22 ⋯ p 29 p 210 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ S ( 9 ) p 91 p 92 ⋯ p 99 p 910 S ( 10 ) p 101 p 102 ⋯ p 109 p 1010 \begin{matrix} &S^{(1)} & S^{(2)}&\cdots & S^{(9)}& S^{(10)} \\ S^{(1)} & p_{11} &p_{12}& \cdots & p_{19}& p_{110} \\ S^{(2)} & p_{21}&p_{22}&\cdots&p_{29}&p_{210}\\ \vdots & \vdots&\vdots & \ddots & \vdots &\vdots\\ S^{(9)} & p_{91}&p_{92} & \cdots & p_{99} &p_{910} \\ S^{(10)}&p_{101}&p_{102}&\cdots&p_{109}&p_{1010} \end{matrix} S(1)S(2)⋮S(9)S(10)S(1)p11p21⋮p91p101S(2)p12p22⋮p92p102⋯⋯⋯⋱⋯⋯S(9)p19p29⋮p99p109S(10)p110p210⋮p910p1010
表示各个状态之间转移的概率。
2.2 动态函数/动态特性
对于离散的变量,可以用状态转移矩阵表示,但是对于连续的随机变量,只能用函数来表示,称为动态函数,也可以叫做MDP的动态特性,用花体 P \mathcal{P} P来表示
- 定义
P : p ( s ′ , r ∣ s , a ) = P r { S t + 1 = s ′ , R t + 1 = r ∣ S t = s , A t = a } \mathcal{P}: p(s',r|s,a)=P_r\{S_{t+1}=s',R_{t+1}=r|S_t=s,A_t=a\} P:p(s′,r∣s,a)=Pr{St+1=s′,Rt+1=r∣St=s,At=a}
上面的函数也可以称作状态转移函数,但是存在奖励
r
r
r,成为状态转移函数可能不是很贴切,可以次采用下面的状态转移函数的定义:
p
(
s
′
∣
s
,
a
)
=
P
r
{
S
t
+
1
=
s
′
∣
S
t
=
s
,
A
t
=
a
}
p(s'|s,a)=P_r\{S_{t+1}=s'|S_t=s,A_t=a\}
p(s′∣s,a)=Pr{St+1=s′∣St=s,At=a}
【表达方式】
- 一般随机变量都用大写字母表示,随机变量具体的取值用小写字母表示,比如表示某个概率: P { X = s } = 0.6 P\{X=s\}=0.6 P{X=s}=0.6
【注意点】
- 上面所说的定义中,奖励R也是一个随机变量,比如说第1次在状态s时,采取动作a得到的r=0.8;第100次正好也是状态s,再采取同样的动作啊,得到的奖励就有可能是r=0.4了。
2.3 价值函数 · Value Function
2.3.1 策略
Policy: 用 π \pi π来表示,分为以下两种:
- 确定性策略
只要出现了状态s,我就选择行为a,跟时间没有关系,只跟状态有关系。
a = π ( s ) a=\pi(s) a=π(s) - 随机性策略
选择哪一种行为a1,a2,a3…是有一定概率的。
π ( a ∣ s ) = P r { A t = a ∣ S t = s } \pi(a|s)=P_r\{A_t=a|S_t=s\} π(a∣s)=Pr{At=a∣St=s}
2.3.2 回报
回报指的是在当前状态 s s s下,做出动作 a a a之后,得到的即时奖励 R t + 1 R_{t+1} Rt+1以及后面一系列的奖励 R t + 2 、 R t + 3 、 R t + 4 … … R_{t+2}、R_{t+3}、R_{t+4}…… Rt+2、Rt+3、Rt+4……等等,因为当前的所做出的行为肯定会对以后的一系列状态都构成影响。用 G t G_t Gt表示回报 G t = R t + 1 + R t + 2 + R t + 3 + R t + 4 … … ( 不 是 最 终 形 态 ) G_t=R_{t+1}+R_{t+2}+R_{t+3}+R_{t+4}……(不是最终形态) Gt=Rt+1+Rt+2+Rt+3+Rt+4……(不是最终形态)
【例子】
如果说张三对李四构成了伤害,当天伤害程度肯定是最大的,但是随着时间的推移,伤害这件事对李四虽然一直有影响,但是影响越来越小,所以引入折扣(Discount)的概念。
2.3.3 折扣 · Discount
根据上面的描述,引入折扣
γ
\gamma
γ之后,回报函数为:
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
γ
3
R
t
+
4
+
…
+
γ
T
−
1
R
t
+
T
=
∑
i
=
0
∞
γ
i
R
t
+
1
+
i
(
T
→
∞
)
G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3R_{t+4}+…+\gamma^{T-1}R_{t+T}=\sum_{i=0}^{\infty}\gamma^iR_{t+1+i}(T\rightarrow\infty)
Gt=Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+…+γT−1Rt+T=i=0∑∞γiRt+1+i(T→∞)其中,
γ
∈
[
0
,
1
]
\gamma\in[0,1]
γ∈[0,1]
2.3.4 价值函数 · Value Function
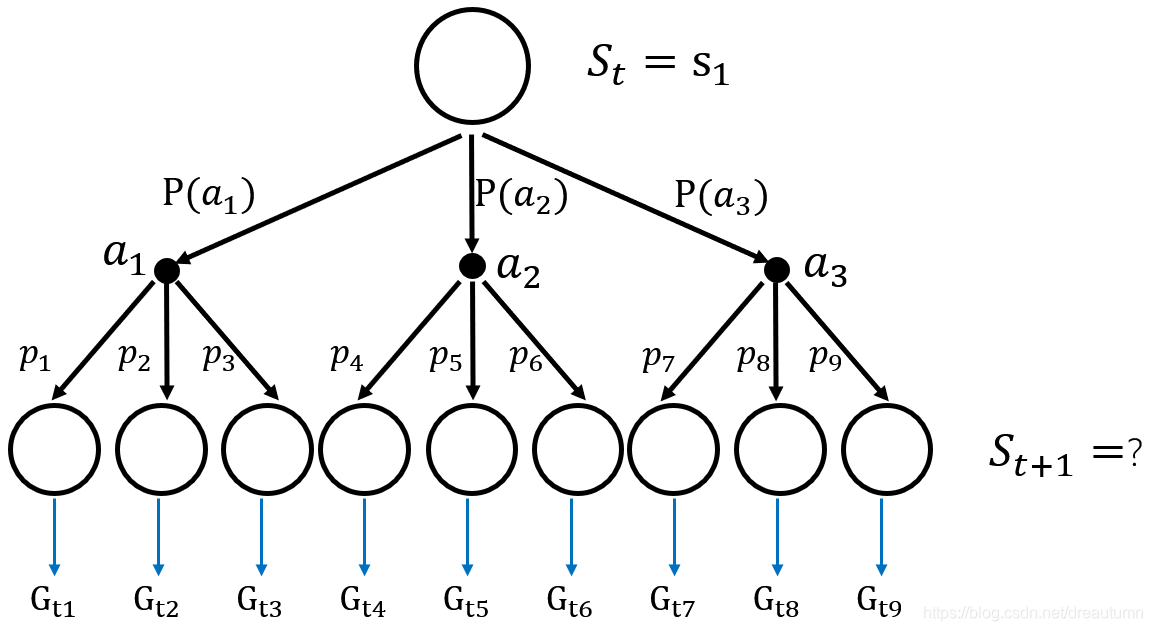
考虑到实际的决策过程,假设只有三个状态 S = { s 1 , s 2 , s 3 } S=\{s_1,s_2,s_3\} S={s1,s2,s3},也只有三个行为 A = { a 1 , a 2 , a 3 } A=\{a_1,a_2,a_3\} A={a1,a2,a3},如下图所示,从状态 S t → S t + 1 S_t\rightarrow S_{t+1} St→St+1,可能采取三种行为中的一种,而采取每种行为之后,又根据每种行为的状态转移概率进行到下一个状态,因此一共有九种可能性,故算起回报函数会非常的麻烦,因此引入价值函数的概念
-
状态价值函数
价值函数定义为,在采取策略 π \pi π的前提下,所有可能的 G t G_t Gt的加权平均值,即为期望值。 V π ( s ) = E π [ G t ∣ S t = s ] V_\pi(s)=E_\pi[G_t|S_t=s] Vπ(s)=Eπ[Gt∣St=s] -
状态动作价值函数
q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=E_\pi[G_t|S_t=s,A_t=a] qπ(s,a)=Eπ[Gt∣St=s,At=a]
【辨析】
- 策略 π \pi π存在的意义就是为了管理状态 s s s和行为 a a a之间的关系
π : s → a \pi:s\rightarrow a π:s→a
意思就是在 π \pi π的约束下,s和a是一一对应的。- V π ( s ) V_\pi(s) Vπ(s)的初始条件只有s,表示t时刻采取了策略 π \pi π,进而所能得到的奖励。在t时刻采取的行为a以及之后采取的行为a均由策略 π \pi π决定。
- q π ( s , a ) q_\pi(s,a) qπ(s,a)的初始条件有s和a,同样表示t时刻采取了策略 π \pi π,进而所能得到的奖励。但是在t时刻采取的行为a是已经给定的,跟策略 π \pi π没有关系,策略 π \pi π只能决定从t+1时刻开始的行为a。
3 贝尔曼期望方程 · Bellman Expectation Equation
3.1 V π ( s ) V_\pi(s) Vπ(s)和 q π ( s , a ) q_\pi(s,a) qπ(s,a)的关系
根据上面的论述,还是假设只有三个状态 S = { s 1 , s 2 , s 3 } S=\{s_1,s_2,s_3\} S={s1,s2,s3},也只有三个行为 A = { a 1 , a 2 , a 3 } A=\{a_1,a_2,a_3\} A={a1,a2,a3},一共有9种可能的情况,也就有9个 G t G_t Gt。
-
V π ( s ) V_\pi(s) Vπ(s)就是这9个 G t G_t Gt的加权平均值(期望)
V π ( s ) = G t 1 ⋅ P ( a 1 ) ⋅ p 1 + G t 2 ⋅ P ( a 1 ) ⋅ p 2 + G t 3 ⋅ P ( a 1 ) ⋅ p 3 + G t 4 ⋅ P ( a 2 ) ⋅ p 4 + G t 5 ⋅ P ( a 2 ) ⋅ p 5 + G t 6 ⋅ P ( a 2 ) ⋅ p 6 + G t 7 ⋅ P ( a 3 ) ⋅ p 7 + G t 8 ⋅ P ( a 3 ) ⋅ p 8 + G t 9 ⋅ P ( a 3 ) ⋅ p 9 (3-1) \begin{aligned} V_\pi(s)=&G_{t1}·P(a_1)·p_1+G_{t2}·P(a_1)·p_2+G_{t3}·P(a_1)·p_3+\\ &G_{t4}·P(a_2)·p_4+G_{t5}·P(a_2)·p_5+G_{t6}·P(a_2)·p_6+\\ &G_{t7}·P(a_3)·p_7+G_{t8}·P(a_3)·p_8+G_{t9}·P(a_3)·p_9 \tag{3-1} \end{aligned} Vπ(s)=Gt1⋅P(a1)⋅p1+Gt2⋅P(a1)⋅p2+Gt3⋅P(a1)⋅p3+Gt4⋅P(a2)⋅p4+Gt5⋅P(a2)⋅p5+Gt6⋅P(a2)⋅p6+Gt7⋅P(a3)⋅p7+Gt8⋅P(a3)⋅p8+Gt9⋅P(a3)⋅p9(3-1)
其中, G t x G_{tx} Gtx表示的9种情况的回报, P ( a x ) P(a_x) P(ax)表示的是选择某个行为a的概率, p x p_x px表示的是在确定好行为a之后,由状态转移函数决定的选到某个具体的 G t x G_{tx} Gtx的概率。
-
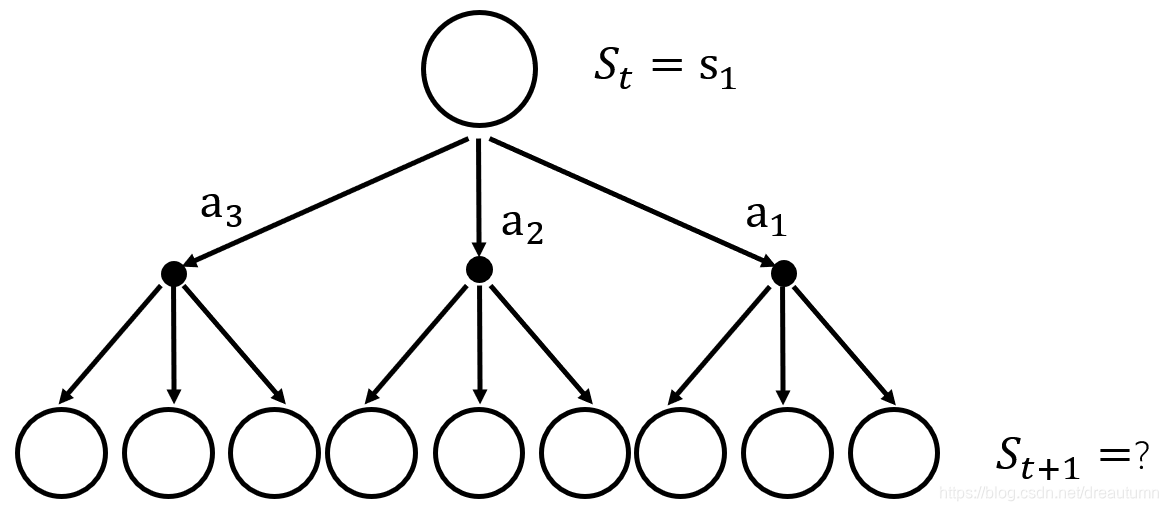
q π ( s , a ) q_\pi(s,a) qπ(s,a)就是这9个 G t G_t Gt中的其中3个 G t G_t Gt的加权平均值
q π ( s , a 1 ) = G t 1 ⋅ p 1 + G t 2 ⋅ p 2 + G t 3 ⋅ p 3 q π ( s , a 2 ) = G t 4 ⋅ p 4 + G t 5 ⋅ p 5 + G t 6 ⋅ p 6 q π ( s , a 3 ) = G t 7 ⋅ p 7 + G t 8 ⋅ p 8 + G t 9 ⋅ p 9 (3-2) q_\pi(s,a_1)=G_{t1}·p_1+G_{t2}·p_2+G_{t3}·p_3\\ q_\pi(s,a_2)=G_{t4}·p_4+G_{t5}·p_5+G_{t6}·p_6\\ q_\pi(s,a_3)=G_{t7}·p_7+G_{t8}·p_8+G_{t9}·p_9\tag{3-2} qπ(s,a1)=Gt1⋅p1+Gt2⋅p2+Gt3⋅p3qπ(s,a2)=Gt4⋅p4+Gt5⋅p5+Gt6⋅p6qπ(s,a3)=Gt7⋅p7+Gt8⋅p8+Gt9⋅p9(3-2)
比较公式3-1和3-2可知,
V
π
(
s
)
V_\pi(s)
Vπ(s)和
q
π
(
s
,
a
)
q_\pi(s,a)
qπ(s,a)存在以下关系:
V
π
(
s
)
=
q
π
(
s
,
a
1
)
⋅
P
(
a
1
)
+
q
π
(
s
,
a
2
)
⋅
P
(
a
2
)
+
q
π
(
s
,
a
3
)
⋅
P
(
a
3
)
V_\pi(s)=q_\pi(s,a_1)·P(a_1)+q_\pi(s,a_2)·P(a_2)+q_\pi(s,a_3)·P(a_3)
Vπ(s)=qπ(s,a1)⋅P(a1)+qπ(s,a2)⋅P(a2)+qπ(s,a3)⋅P(a3)
而
P
(
a
x
)
P(a_x)
P(ax)的值是由
π
(
a
∣
s
)
\pi(a|s)
π(a∣s)确定的,上面只有9种情况,拓展到无限种可能,可以得到
V
π
(
s
)
V_\pi(s)
Vπ(s)和
q
π
(
s
,
a
)
q_\pi(s,a)
qπ(s,a)的关系为:
V
π
(
s
)
=
∑
a
∈
A
q
π
(
s
,
a
)
⋅
π
(
a
∣
s
)
(3-3)
V_\pi(s)=\sum_{a\in \mathcal{A}} q_\pi (s,a)·\pi(a|s) \tag{3-3}
Vπ(s)=a∈A∑qπ(s,a)⋅π(a∣s)(3-3)





 博客介绍了随机变量、随机过程、马尔可夫链/过程等概念,阐述了状态空间模型、马尔可夫奖励过程和马尔可夫决策过程的构成。还分析了马尔可夫相关的动态特性,包括状态转移矩阵、动态函数,介绍了价值函数、策略、回报和折扣等内容,最后探讨了贝尔曼期望方程中Vπ(s)和qπ(s,a)的关系。
博客介绍了随机变量、随机过程、马尔可夫链/过程等概念,阐述了状态空间模型、马尔可夫奖励过程和马尔可夫决策过程的构成。还分析了马尔可夫相关的动态特性,包括状态转移矩阵、动态函数,介绍了价值函数、策略、回报和折扣等内容,最后探讨了贝尔曼期望方程中Vπ(s)和qπ(s,a)的关系。



















 6092
6092

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










