前言
明明研究方向是图形学,现在也开始朝着深度学习卷了。
以前或多或少了解和使用过一些深度学习方法,但都是处于一知半解的状态,现在开始系统地学习各种深度学习的网络和方法,并记录下学习笔记。
神经元
**神经网络(Neural Networks)**的定义:神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应 [Kohonen, 1988]。
神经网络的基本组成单元就是**神经元(Neuron)**模型。在生物神经网络中,每个神经元都与其它若干个神经元相连,神经元有多条树突(Dendrite)作为信号的输入,一条轴突(Axon)作为信号的输出。当“输入信号”导致神经元的电位超过一个阈值(Threshold)时,它就会被激活,并向其它神经元传递信号。
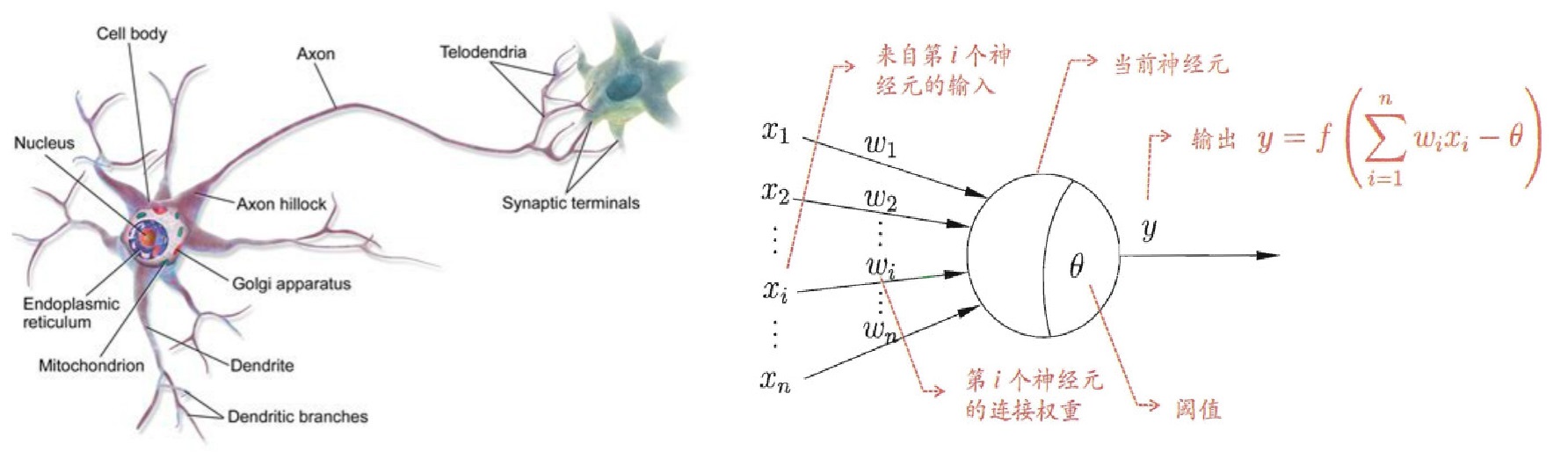
生物神经元进行抽象就得到了上图(右)所示的**M-P神经元(McCulloch-Pitts Neuron)模型。模型中神经元接收来自nnn个其它神经元传递过来的输入信号,输入信号通过带权重的连接(Connection)进行传递,神经元将输入值的加权和与阈值比较,然后用激活函数(Activation Function)**输出。
常用的激活函数:f(x)=sigmoid(x)=11+e−xf(x)=sigmoid(x)=\frac{1}{1+e^{-x}}f(x)=sigmoid(x)=1+e−x1。
感知机与多层网络(前馈神经网络)
M-P神经元也可作为感知机(Perceptron)使用,对于阈值θ\thetaθ,可以看成固定输入−1-1−1,权重为ωn+1\omega_{n+1}ωn+1。感知机的训练规则为,对于训练样例(x,y)(\mathbf{x},y)(x,y),输出为y^\hat{y}y^,则将权重这样调整:
ωi←ωi+η(y−y^)xi(1)
\omega_i \leftarrow \omega_i+\eta(y-\hat{y})x_i
\tag{1}
ωi←ωi+η(y−y^)xi(1)
其中η\etaη称为学习率(Learning Rate)。
如果两类模式是线性可分的,那么感知机的学习过程一定会收敛。
对于其它问题,需要考虑使用多层神经元。常见的神经网络是如下图所示的层级结构,每层神经元与下一层神经元“全互连”,神经元之间不存在同层连接或跨层连接。这样的神经网络结构称为多层前馈神经网络(Multi-layer Feedforward Neural Networks),与感知机一起也合称为前馈神经网络(FNN),或称为多层感知机(MLP)。

FNN的第一层为输入层,不对数据进行任何处理,最后一层为输出层,中间的为隐层或隐含层(Hidden Layer),输出层和隐含层都会进行激活函数处理。学习的过程就是对层之间的权重更新的过程,学到的东西蕴含在连接权重之中。
误差逆传播
对于多层神经网络,其训练过程中更新权重的规则常用**误差逆传播(BackPropagation, BP)**算法。
给定训练集D={(x1,y1),…,(xm,ym)},xi∈Rd,yi∈RlD=\{(\mathbf{x}_1,\mathbf{y}_1),\dots,(\mathbf{x}_m,\mathbf{y}_m)\},\mathbf{x}_i\in\mathbb{R}^d,\mathbf{y}_i\in\mathbb{R}^lD={(x1,y1),…,(xm,ym)},xi∈Rd,yi∈Rl,输入为ddd维向量,输出为lll维向量,我们讨论某一个训练样例(xk,yk)(\mathbf{x}_k,\mathbf{y}_k)(xk,yk),假设FNN的输出为y^k=(y^1k,…,y^lk)\hat{\mathbf{y}}_k=(\hat{y}_1^k,\dots,\hat{y}_l^k)y^k=(y^1k,…,y^lk),则网络在这个训练样例上的均方误差为
Ek=12∑j=1l(y^jk−yjk)2,(2)
E_k=\frac{1}{2}\sum_{j=1}^{l}(\hat{y}_j^k-y_j^k)^2 ,
\tag{2}
Ek=21j=1∑l(y^jk−yjk)2,(2)
那么从一个一般意义的角度来讲,网络学习的目的是要使得误差EkE_kEk尽可能小,因此我们要将参数(权重)沿着梯度的反方向移动,这就是**梯度下降(Gradient Descent)**的策略。从数值计算的角度来看,对于某个连接权重www,其更新公式为
w←w−η∂Ek∂w。(3)
w\leftarrow w-\eta\frac{\partial E_k}{\partial w} 。
\tag{3}
w←w−η∂w∂Ek。(3)
以上就是BP算法的全部内容,下面通过包含一个隐层的FNN的例子来详细说明BP的过程。

上图是一个FNN的例子,需要补充说明的是,bhb_hbh表示了隐层的输出,θj\theta_jθj是输出层神经元的阈值,隐层和输出层神经元都使用Sigmoid激活函数。同样假定神经网络的输出为y^k=(y^1k,…,y^lk)\hat{\mathbf{y}}_k=(\hat{y}_1^k,\dots,\hat{y}_l^k)y^k=(y^1k,…,y^lk),我们考察隐层和输出层之间的某个权值whjw_{hj}whj的更新,注意whjw_{hj}whj和EkE_kEk之间是复合函数的关系,因此有
∂Ek∂whj=∂Ek∂y^jk⋅∂y^jk∂βj⋅∂βj∂whj,(4)
\frac{\partial{E_k}}{\partial{w_{hj}}}=\frac{\partial{E_k}}{\partial{\hat{y}^k_j}} \cdot \frac{\partial{\hat{y}^k_j}}{\partial{\beta_j}} \cdot \frac{\partial{\beta_j}}{\partial{w_{hj}}} ,
\tag 4
∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj,(4)
其中∂βj∂whj=bh\frac{\partial{\beta_j}}{\partial{w_{hj}}}=b_h∂whj∂βj=bh以及∂Ek∂y^jk=(y^jk−yjk)\frac{\partial{E_k}}{\partial{\hat{y}^k_j}}=(\hat{y}^k_j-y^k_j)∂y^jk∂Ek=(y^jk−yjk)是很容易求得的,中间那个偏导数是对Sigmoid函数y^jk=f(βj−θj)\hat{y}_j^k=f(\beta_j-\theta_j)y^jk=f(βj−θj)求,而Sigmoid函数有个性质就是f′(x)=f(x)(1−f(x))f'(x)=f(x)(1-f(x))f′(x)=f(x)(1−f(x)),因此∂y^jk∂βj=y^jk(1−y^jk)\frac{\partial{\hat{y}^k_j}}{\partial{\beta_j}}=\hat{y}^k_j(1-\hat{y}^k_j)∂βj∂y^jk=y^jk(1−y^jk),综上可得
∂Ek∂whj=(y^jk−yjk)y^jk(1−y^jk)bh。(5)
\frac{\partial{E_k}}{\partial{w_{hj}}}=(\hat{y}^k_j-y^k_j)\hat{y}^k_j(1-\hat{y}^k_j)b_h。
\tag 5
∂whj∂Ek=(y^jk−yjk)y^jk(1−y^jk)bh。(5)
联立公式(3, 5)就可以实现隐层和输出层之间权重的更新。
对于输入层和隐层之间的权值vihv_{ih}vih,有
∂Ek∂vih=∂Ek∂bh⋅∂bh∂vih,(6)
\frac{\partial{E_k}}{\partial{v_{ih}}}=\frac{\partial{E_k}}{\partial{b_h}}\cdot \frac{\partial{b_h}}{\partial{v_{ih}}},
\tag 6
∂vih∂Ek=∂bh∂Ek⋅∂vih∂bh,(6)
实际上也是链式求导,就是会比(4)长很多。
通过以上例子我们可以知道,FNN的网络层越深,其误差对权值的偏导的链式就越长,考虑Sigmoid函数的导数f′(x)=f(x)(1−f(x))≤(12)2=0.25f'(x)=f(x)(1-f(x))\le (\frac{1}{2})^2=0.25f′(x)=f(x)(1−f(x))≤(21)2=0.25,因此当层数太多时,多个导数的累乘会导致“梯度消失”的现象。与之相反的是梯度爆炸现象,这些都是梯度变化的不稳定性,会使得层数变多时反而学习准确率下降。
全局最小 or 局部极小?
神经网络的训练,可以看成是找到误差函数EEE的最小值的问题,因此不可避免的需要考虑,有可能训练过程只找到了局部极小值,就收敛了。有以下一些方法来“跳出”局部极小:
- 模拟退火技术;
- 以多组不同的数值初始化神经网络,按标准方法训练后,取最优的解;
- 随机梯度下降,计算梯度时加入随机因素,因此即使陷入局部极小点,梯度也不为0,就有机会跳出局部极小点,但后果是可能在最优解附近震荡;
跳出局部极小的方法大多是启发式的,不能保证对任何问题都一定适用。
参考资料
- 周志华-《机器学习》第5章;
- 网络资料。






















 3129
3129

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








