251215-251221集训

目录

周三题单

A.Shashliks（数学）

B.Good Start（数学）

C.Equal Subsequences（脑筋急转弯）

D**.Make It Permutation（数学+reverse）

E.False Alarm（模拟）

F.Shrink（模拟）

G**.Cool Partition（哈希+贪心）

H*.Retaliation（数学+等差数列的判断策略）（最棒的一题！）

等差数列判断策略

周日题单

一、2025（位运算+数学）

二、hacker（位运算+模拟）

三、异或积（位运算+规律）

四、高低位互换（位运算）

五、DEATHSTAR（位运算+模拟）

六、A-B数对（排序+哈希）

七、连续自然数和（暴力+简单优化 /  数学）

八、在你窗外闪耀的星星（滑动窗口）

九、【模板】单调队列/滑动窗口

---

周三题单

A.Shashliks（数学）

Problem - A - Codeforces

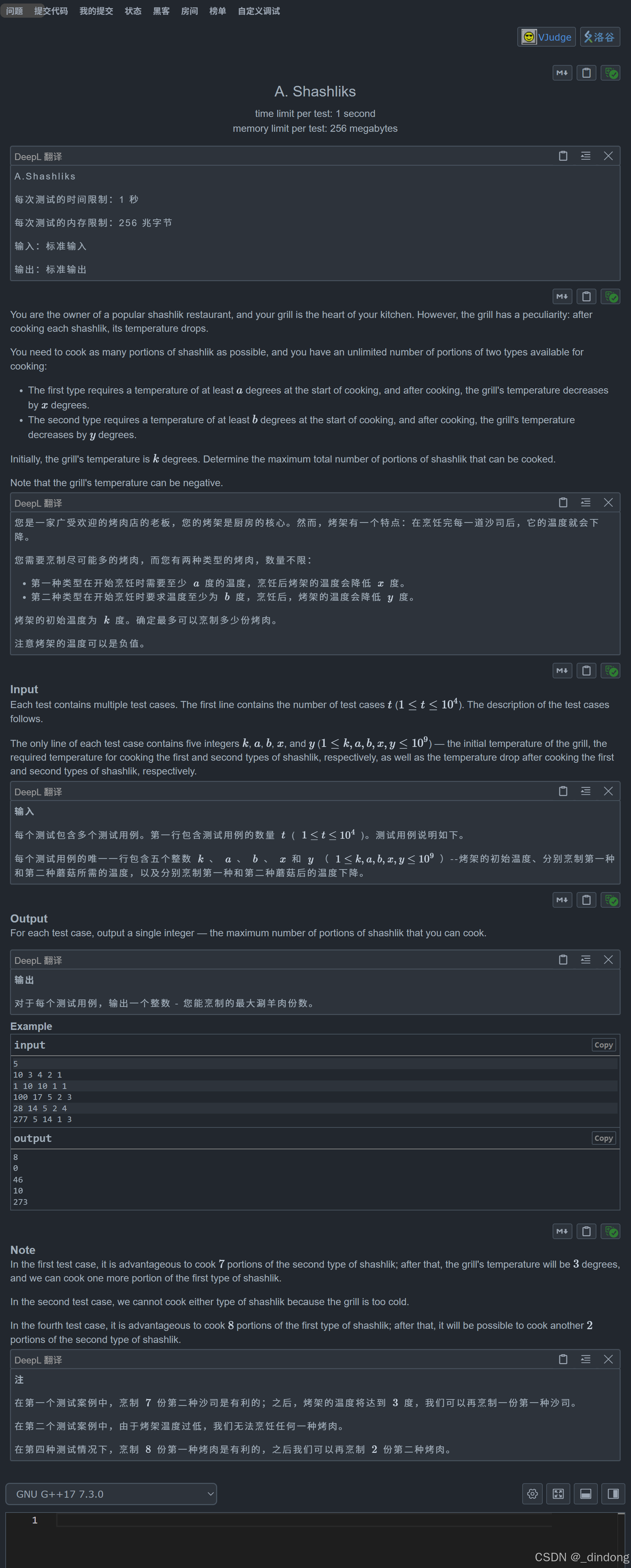
温度满足两个都能烤的时候，烤降温少的那个；只满足一个温度，就烤那一个；否则为0

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int t,k,a,b,x,y;
void solve(int k,int a,int b,int x,int y)
{
    int min_temp=min(a,b),max_temp=max(a,b);
    if (k<min_temp)
    {
        cout<<0<<endl;
        return;
    }

    ll ret=0;
    if (k>=max_temp)
    {
        int min_reduce=min(x,y),gap=k-max_temp;
        ret+=(gap/min_reduce+1);
        k-=ret*min_reduce;
        if (k<min_temp)
        {
            cout<<ret<<endl;
            return;
        }

        if (a<b)
        {
            ret+=((k-a)/x+1);
            cout<<ret<<endl;
            return;
        }
        //b<=a
        ret+=((k-b)/y+1);
        cout<<ret<<endl;
        return;
    }

    //k>=min_temp&&k<max_temp
    if (a<b)
    {
        ret+=((k-a)/x+1);
        cout<<ret<<endl;
        return;
    }
    //b>=a
    ret+=((k-b)/y+1);
    cout<<ret<<endl;
}
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>k>>a>>b>>x>>y;
        solve(k,a,b,x,y);
    }

    return 0;
}

官方题解如下，我们无需判断谁大谁小，按一套逻辑运算，输出更大的那套的值

```
#include <iostream>

using namespace std;

void solve() {
    int t, a, b, x, y;
    cin >> t >> a >> b >> x >> y;
    auto solve = [&](int t, int a, int b, int x, int y) {
        int cur = 0;
        cur += max((t - a + x) / x, 0);
        t -= max((t - a + x) / x, 0) * x;
        cur += max((t - b + y) / y, 0);
        return cur;
    };
    cout << max(solve(t, a, b, x, y), solve(t, b, a, y, x)) << endl;
}

signed main() {
    int q = 1;
    cin >> q;
    while (q --> 0)
        solve();
    return 0;
}```

B.Good Start（数学）

Problem - B - Codeforces

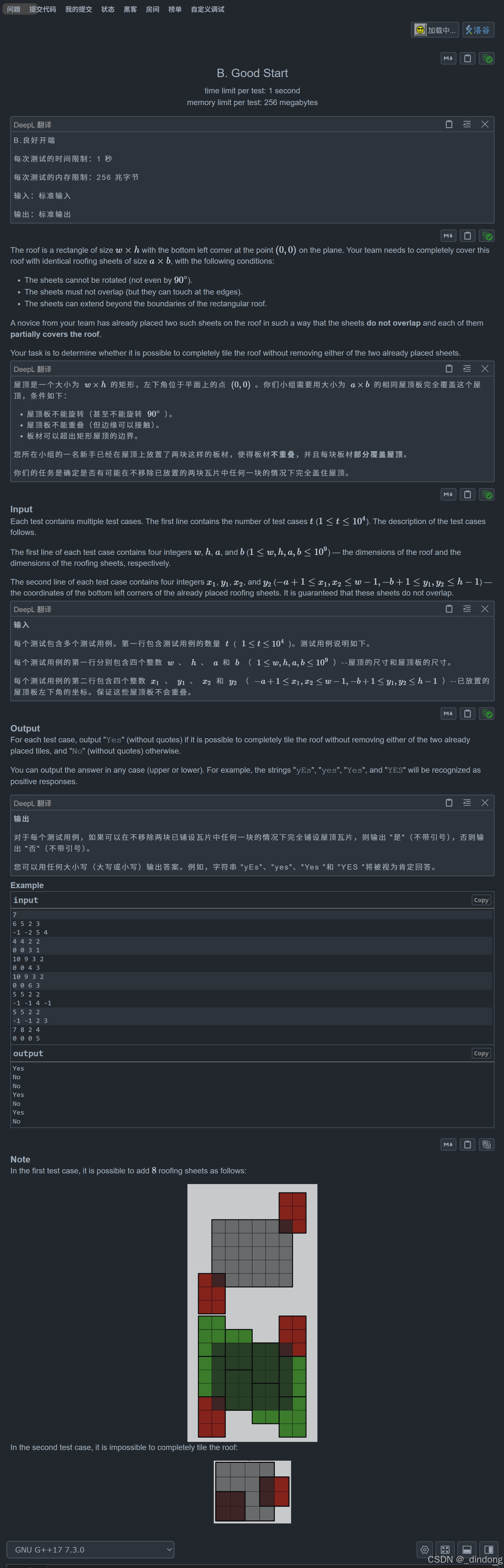
我们只需判断已经放入的两个瓦片的中心区域（下图阴影部分），长和宽取模于a，b是否为0

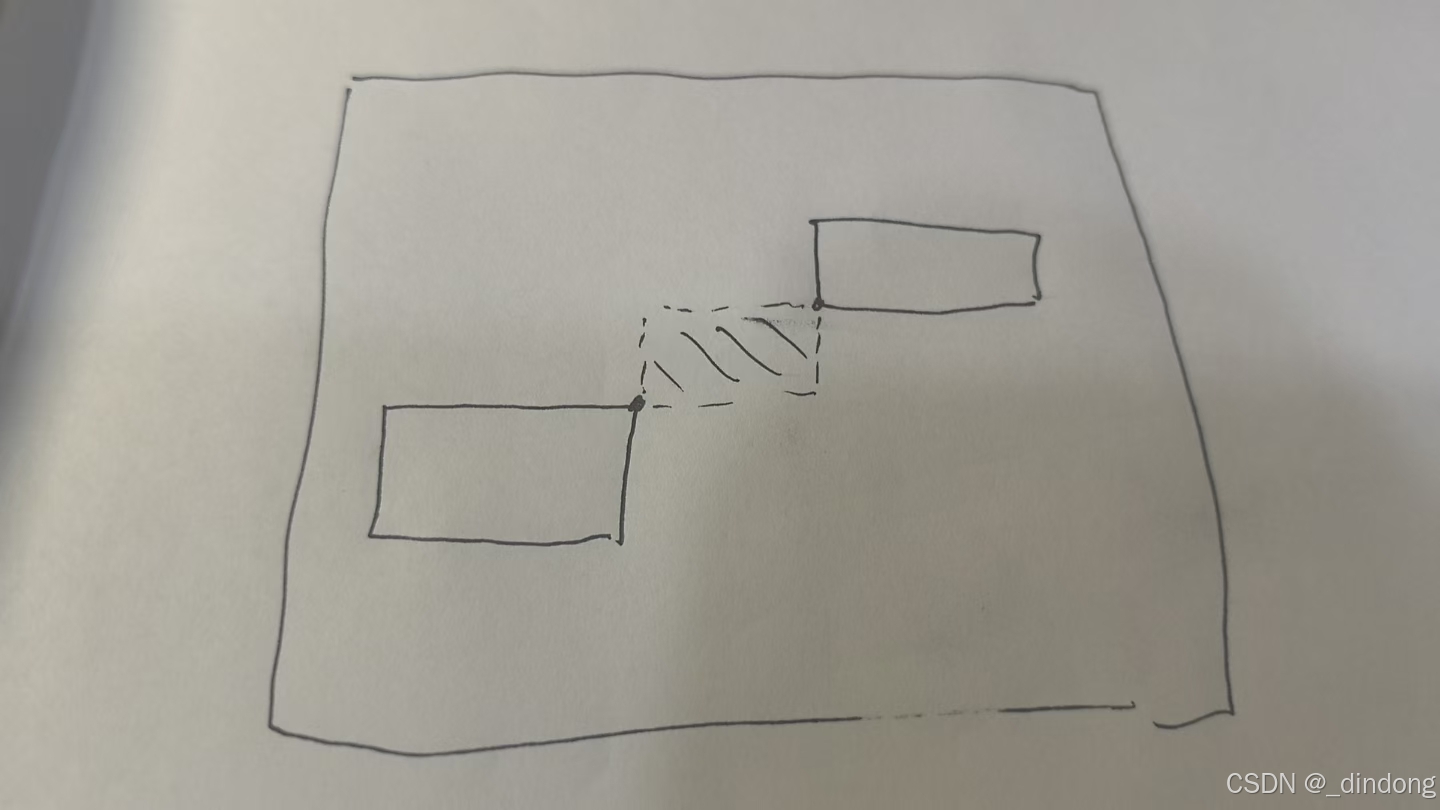
题解如下，可以优化

#include<iostream>
using namespace std;
using ll=long long;
int t,w,h,a,b,x1,y1,x2,y2;


int main()
{
    cin>>t;
    while(t--)
    {
        cin>>w>>h>>a>>b>>x1>>y1>>x2>>y2;
        int nx1=x1+a,nx2=x2+a,ny1=y1+b,ny2=y2+b;
        if (y1==y2||(y1>y2&&y1<y2+b)||(y2>y1&&y2<y1+b))
        {
            int gap=min(abs(x1-nx2),abs(nx1-x2));
            if (gap%a==0)cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
        else if (x1==x2||(x1>x2&&x1<x2+a)||(x2>x1&&x2<x1+a))
        {
            int gap=min(abs(y1-ny2),abs(y2-ny1));
            if (gap%b==0)cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
        else
        {
            int gap1=min(abs(x1-nx2),abs(nx1-x2)),gap2=min(abs(y1-ny2),abs(y2-ny1));
            if (gap1%a==0||gap2%b==0)cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }

    return 0;
}

原判断无需进行后续的大小判断，也不需要考虑x+a之类的大小问题，因为瓦片都是一样的，而且题目也说了不会重叠，我们只需要用最初的x做差，取绝对值即可，代码思路如下：

```
def solve():
    w, h, a, b = map(int, input().split())
    x1, y1, x2, y2 = map(int, input().split())
 
    if x1 == x2:
        if abs(y1 - y2) % b == 0:
            return "Yes"
        else:
            return "No"
 
    if y1 == y2:
        if abs(x1 - x2) % a == 0:
            return "Yes"
        else:
            return "No"
 
    if (x1 - x2) % a == 0 or (y1 - y2) % b == 0:
        return "Yes"
    return "No"
 
t = int(input())
for _ in range(t):
    print(solve())```

C.Equal Subsequences（脑筋急转弯）

Problem - A - Codeforces

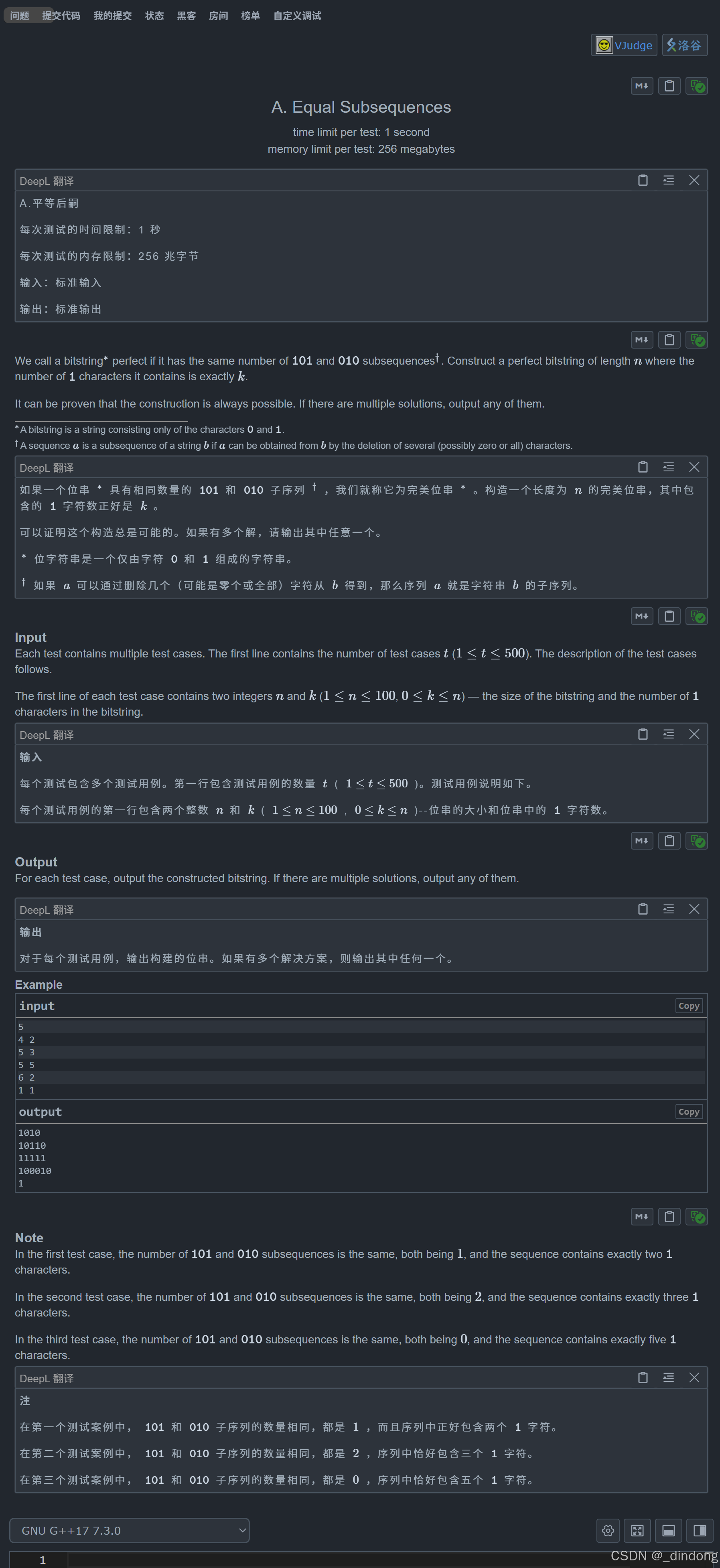
输出k个连续1，剩下的全部输出0，这样101和010子序列的数量都是0，也符合题意

#include<iostream>
using namespace std;
int t,n,k;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>k;
        for (int i=0;i<n-k;i++)cout<<0;
        for (int i=0;i<k;i++)cout<<1;
        cout<<'\n';
    }
    return 0;
}

D**.Make It Permutation（数学+reverse）

Problem - B - Codeforces

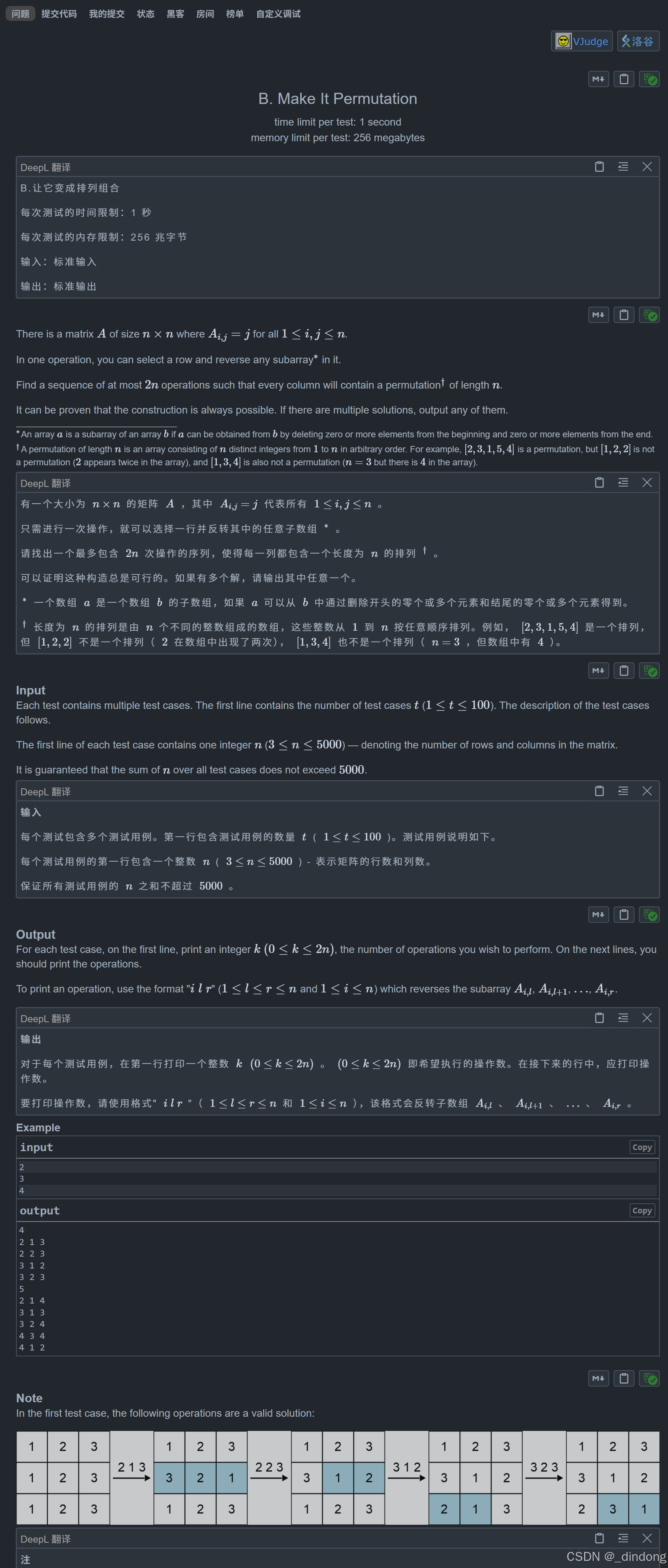
较难实现的一题/(ㄒoㄒ)/~~

题目要求操作次数小于2*n的方案都可以。

曾经做过一题，利用三次逆转，可以将数组元素实现平移，这样，从第二行开始，每行所有元素依次往右移动一格不就解决了。

但是这里要求总次数小于2*n，因为平移操作最后需要reverse整个区间，实际上这一步是不需要的，要完成我们的Make it Permutation只需要“平移”操作的前两步即可。（后来看到题解也是这么写的，不知道是不是按照元素平移那题的思路延申来的）代码实现如下：

#include<bits/stdc++.h>
using namespace std;
int t,n;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        cout<<2*n-3<<'\n';
        for (int i=1;i<n;++i)
        {
            if (i!=1)cout<<i<<" "<<1<<" "<<i<<'\n';
            if (i!=n-1)cout<<i<<" "<<i+1<<" "<<n<<'\n';
        }
        cout<<n<<" "<<1<<" "<<n<<'\n';
    }
    return 0;
}

E.False Alarm（模拟）

Problem - A - Codeforces

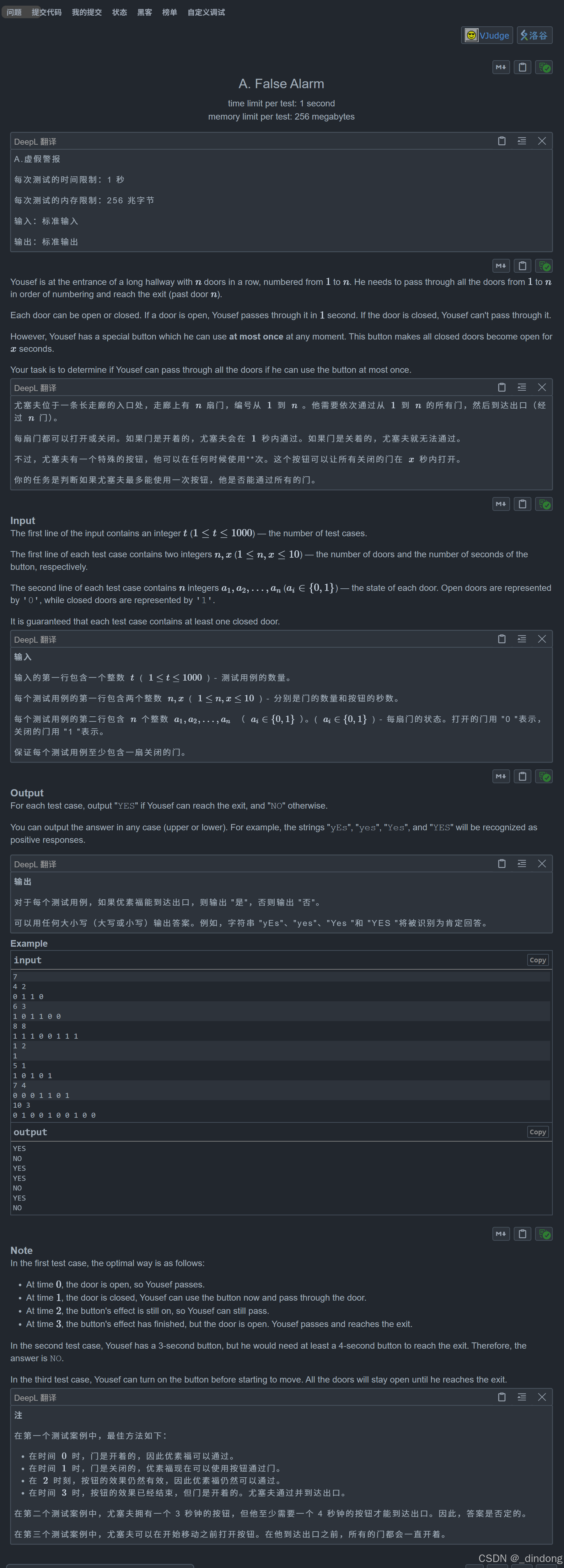
只需要考虑第一个门位置和最后一个门位置即可，很简单

#include<iostream>
using namespace std;
int t,n,x;
int arr[15];
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>x;
        for(int i=1;i<=n;i++)cin>>arr[i];
        int left=1,right=1;
        for (int i=1;i<=n;i++)
        {
            if (arr[i]==1)
            {
                left=i;break;
            }
        }
        for (int i=n;i>=1;i--)
        {
            if (arr[i]==1)
            {
                right=i;break;
            }
        }
        if (right-left>=x)cout<<"NO"<<endl;
        else cout<<"YES"<<endl;
    }
    return 0;
}

F.Shrink（模拟）

Problem - B - Codeforces

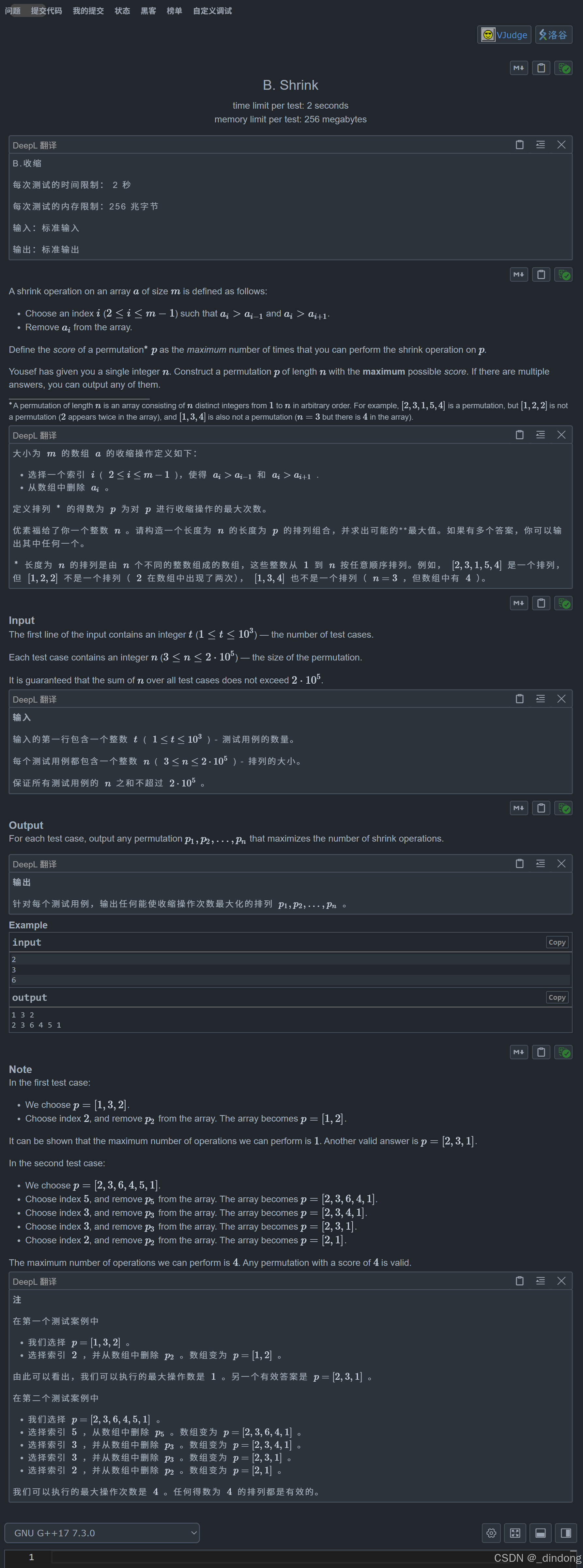
只需要1，2，放在头和尾，中间部分从前往后依次存取n，n-1，n-2...

#include<iostream>
#include <vector>
using namespace std;
int t,n;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        vector<int> a(n);
        a[0]=1,a[n-1]=2;
        int num=n;
        for (int i=1;i<n-1;++i)
        {
            a[i]=num--;
        }
        for (int i=0;i<n-1;++i)cout<<a[i]<<" ";
        cout<<a[n-1]<<endl;
    }
    return 0;
}

G**.Cool Partition（哈希+贪心）

Problem - C - Codeforces

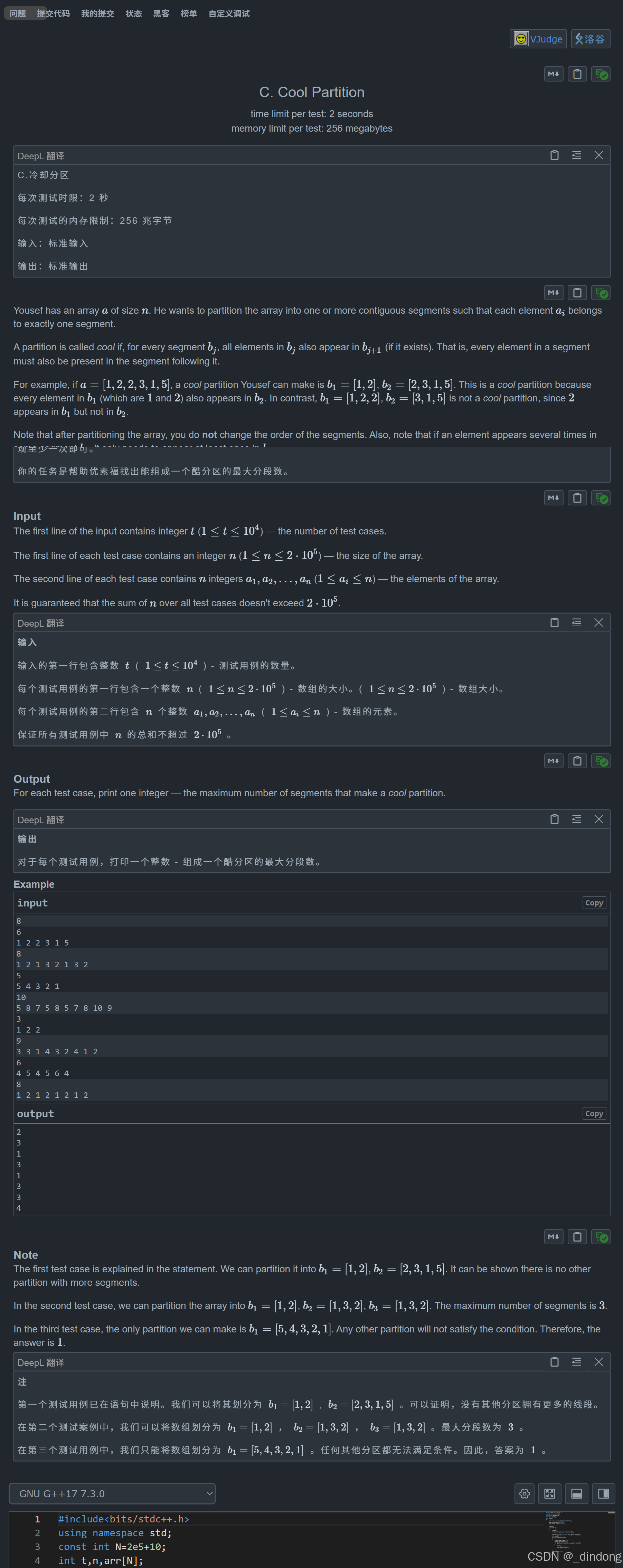
同步增加新旧区间的元素种类个数（利用哈希表），只需判断新区间能否包含前面区间全部元素种类（size相等时）即可，如此分段可以加一

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int t,n,arr[N];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    cin>>t;
    while(t--)
    {
        cin>>n;
        for(int i=0;i<n;i++)cin>>arr[i];

        unordered_map<int,int> past_part,new_part;
        int ans=0;
        for(int i=0;i<n;i++)
        {
            ++past_part[arr[i]];
            ++new_part[arr[i]];
            if (past_part.size()==new_part.size())
            {
                ++ans;
                new_part.clear();
            }
        }
        cout<<ans<<'\n';
    }
    return 0;
}

H*.Retaliation（数学+等差数列的判断策略）（最棒的一题！）

Problem - D - Codeforces

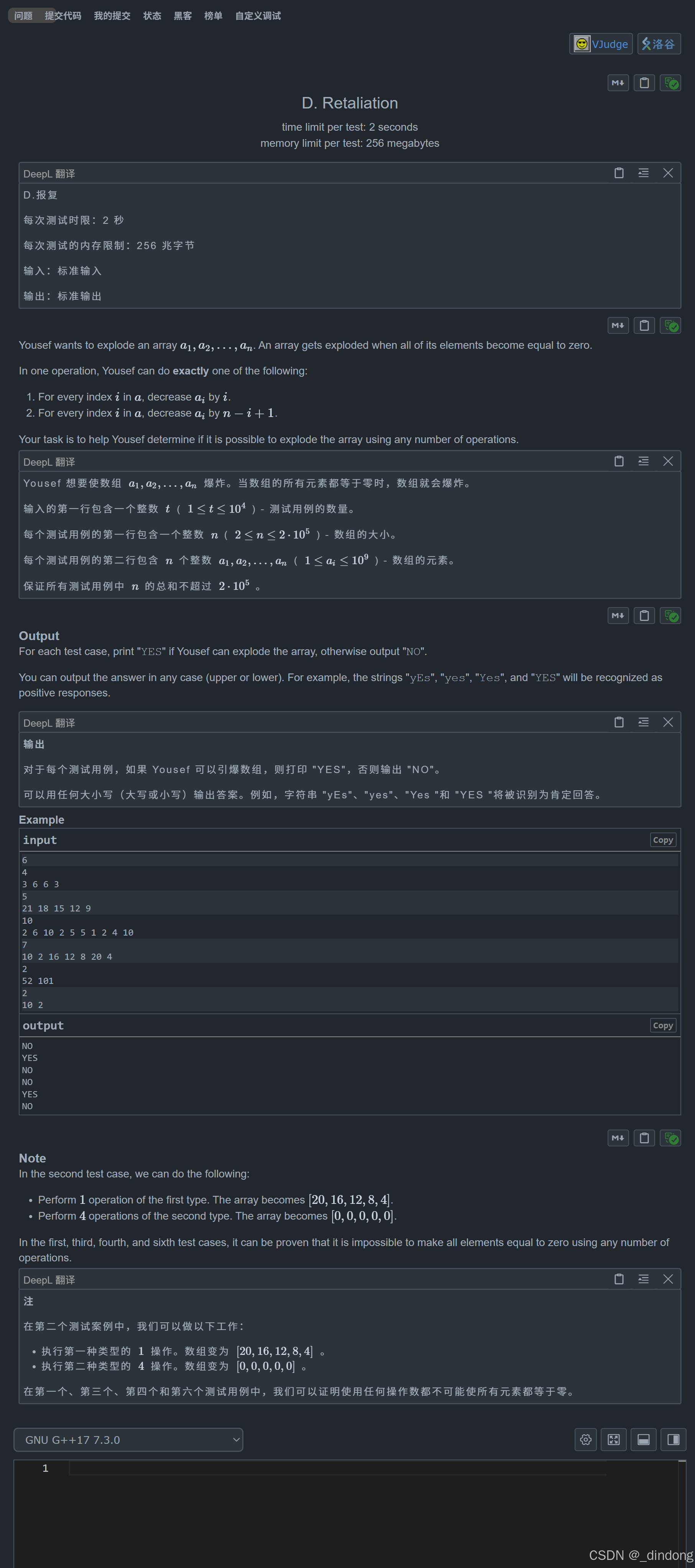
首先可以判断出一定得等差数列，然后根据题意每次选择可以使数组内 i 坐标对应元素减少 i 或者是 n-i+1。这样每次减少，因为坐标间隔 1， 相邻元素的相差值就会逐步缩小 ， 而当执行了公差次数的这种操作后，相差值就会为 0。此时等差数列所有元素全部相等，等于这个数列的最底端的基准点。如果这个基准点≥0，并且取模（n+1）为 0，那么每个元素可以减去 i 再减去 n-i+1，交替操作最终所有元素全部为 0，完成爆破。

最匪夷所思的就是题干里的坐标 i 的元素可以减去 i 或者 n-i+1。这不仅能推出是等差数列，还在提示基准值（>=0&&可以取模(n+1)得0的某个数）存在。

可以画成如下图理解：

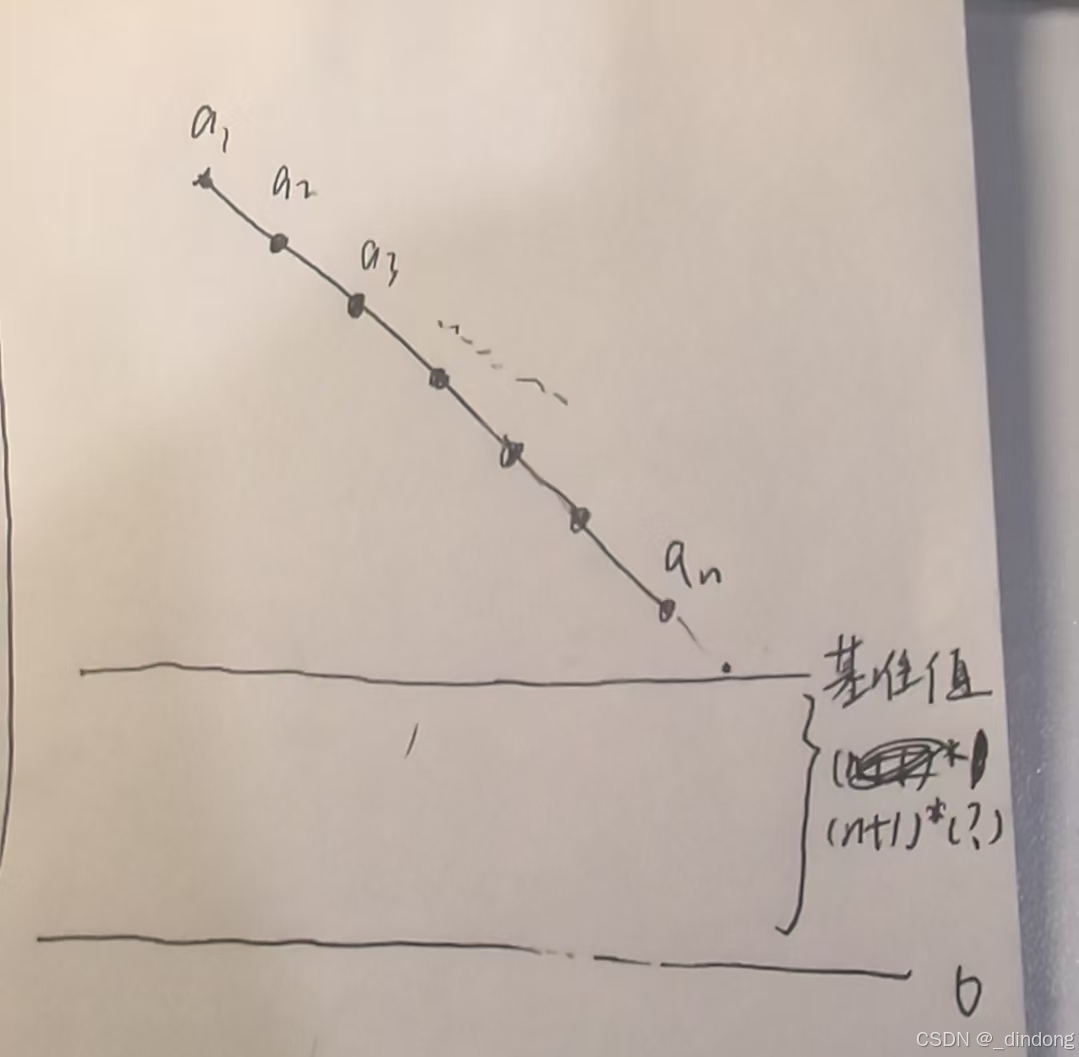
等差数列判断策略

先根据前两个元素求出 d，然后先判断是不是等差，不是等差直接返回。

如果是等差，d 就是公差。对于形如ai=i*d+b的等差数列，让每个元素减去 i 乘上 d，然后取模 b 看下是不是 0，不需要手算求公式了一个一个比对。

代码实现如下：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int arr[N],t,n;
void solve()
{
    int differ=arr[2]-arr[1];
    for (int i=3;i<=n;++i)
    {
        if (arr[i]-arr[i-1]!=differ)
        {
            cout<<"NO"<<'\n';
            return;
        }
    }
    //让所有元素变成基准值
    // for (int i=1;i<=n;++i)
    // {
    //     arr[i]+=(differ<0?differ*(n-i+1):-differ*i);
    // }
    
    //因为等差已经成立了，只让arr[1]变成基准值判断也行
    arr[1]+=(differ<0?differ*n:-differ);
    cout<<( arr[1]>=0&&arr[1]%(n+1)==0? "YES":"NO")<<'\n';
}

int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        for(int i=1;i<=n;i++)cin>>arr[i];
        solve();
    }
    return 0;
}

周日题单

一、2025（位运算+数学）

B4261 [GESP202503 三级] 2025 - 洛谷

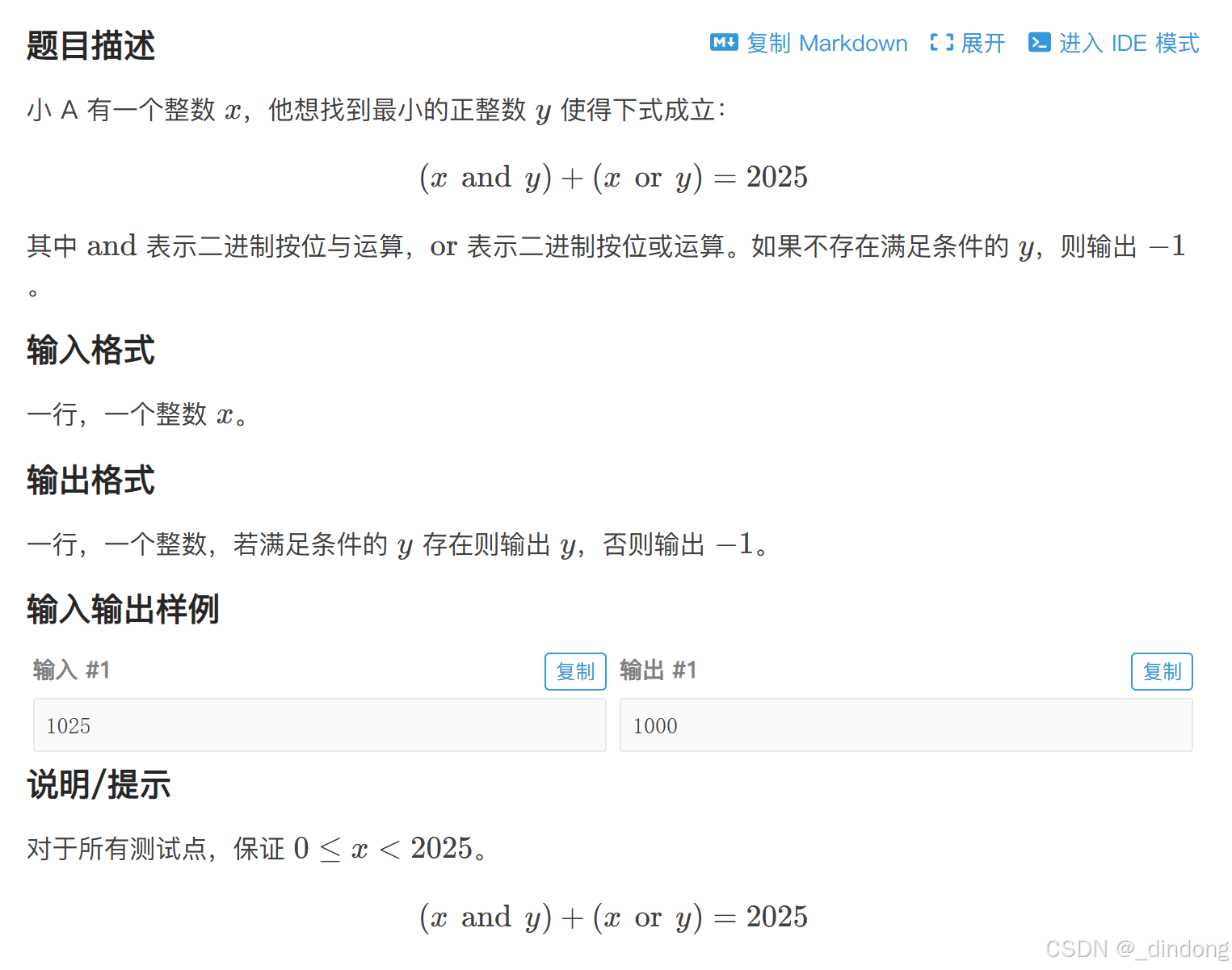
（x&y）+(x^y)==x+y

#include <bits/stdc++.h>
using namespace std;
int t;
int main()
{
    std::ios::sync_with_stdio(0);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    cin>>t;
    cout<<2025-t;

    return 0;
}

二、hacker（位运算+模拟）

P9496 「RiOI-2」hacker - 洛谷

我的解法：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
ll t,n,m;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        if (n==m)
        {
            cout<<0<<endl;
            continue;
        }

        bool case1=false,case2=false;
        while (n&&m)
        {
            if ((n&1)!=(m&1))
            {
                if (n&1==1)case2=true;//需要置0
                else case1=true;
            }

            if (case1&&case2)break;
            n>>=1;
            m>>=1;
        }

        if (case1&&case2)cout<<2<<endl;
        else if (case1&&n)cout<<2<<endl;
        else if (case2&&m)cout<<2<<endl;
        else cout<<1<<endl;
    }

    return 0;
}

评论区更好的题解：

当只有1部分不同，和只有0部分不同到时候，或运算结果会等于二者中的一个

#include<bits/stdc++.h>
using namespace std;
int T;
long long n,m;
int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%lld%lld",&n,&m);
		if(n==m){
			printf("0\n");
			continue;
		}
		if((n|m)==n||(n|m)==m){
			printf("1\n");
		}else{
			printf("2\n");
		}
	}
	return 0;
}

三、异或积（位运算+规律）

P9227 异或积 - 洛谷

打下草稿就能发现，如果n为奇数，进行一次操作后，无论重复几次都和第一次操作情况相同。如果n为偶数，那么数组也就两个状态，操作次数%2==1时，就是操作一次后的情况，%2==0的时候就是原数组的情况。对于异或积，我们可以在输入数组的时候就处理好所有元素的异或积，然后对arr[i]位置用所有元素异或积or上arr[i]就得到了该位置的异或积。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
ll t,n,k;
unsigned int arr[N];
void solve()
{
    cin>>n>>k;
    k%=2;
    unsigned int xorsum=0;
    for ( int i=0;i<n;i++)
    {
        cin>>arr[i];
        xorsum^=arr[i];
    }
    if (n%2==0&&k%2==0)
    {
        for (int i=0;i<n-1;i++)cout<<arr[i]<<" ";
        cout<<arr[n-1]<<endl;
        return;
    }

    for (int i=0;i<n-1;i++)cout<<(xorsum^arr[i])<<" ";
    cout<<(xorsum^arr[n-1])<<endl;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    cin>>t;
    while(t--)
    {
        solve();
    }

    return 0;
}

四、高低位互换（位运算）

P1100 高低位交换 - 洛谷

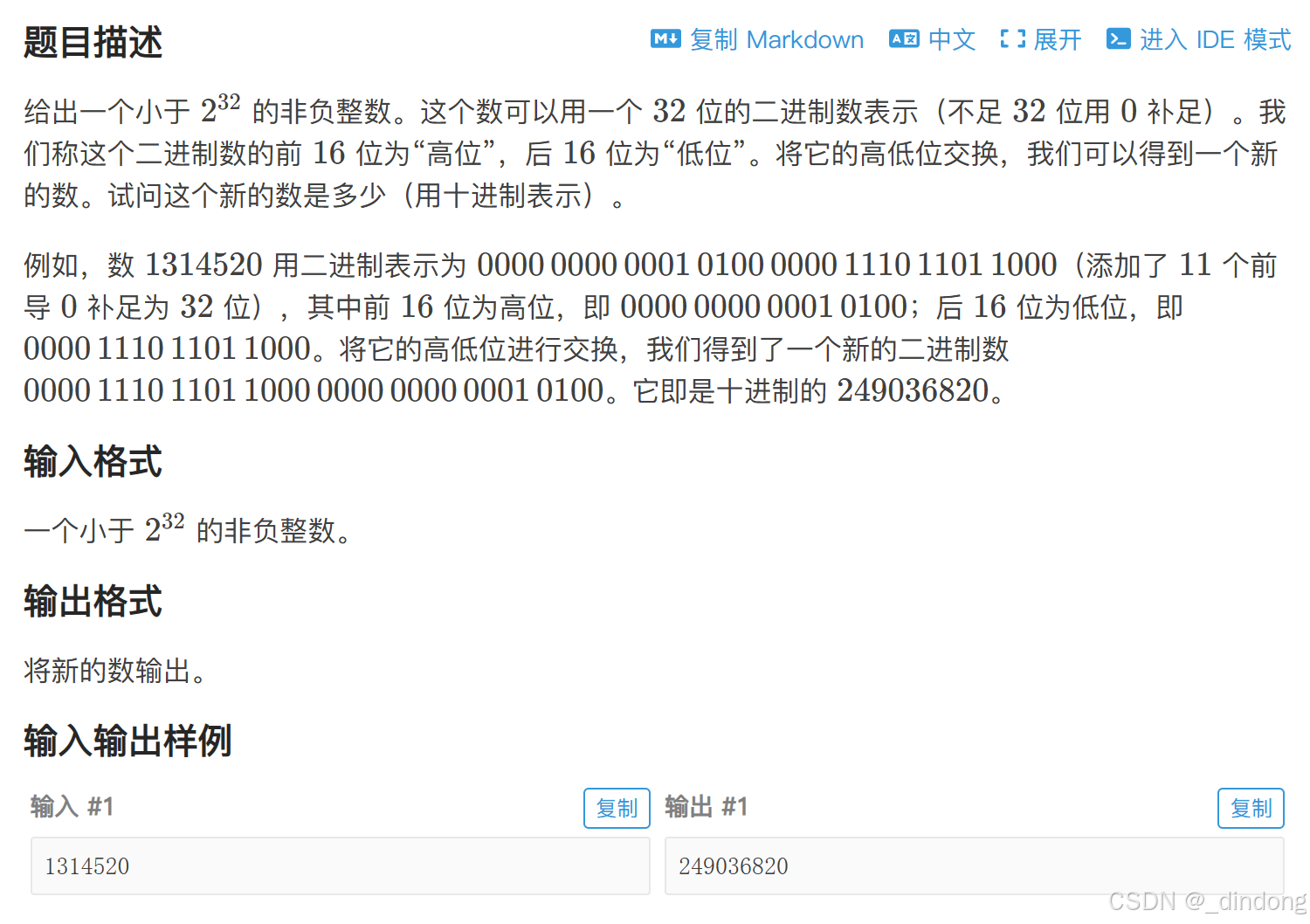
简单的位运算，取16位数后，把低位左移16位，加上右移16位的原数

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
unsigned int x;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    cin>>x;
    unsigned int num=0,tmp=x;
    int cnt=0;
    while (x&&cnt<16)
    {
        if (x&1)num+=pow(2,cnt);
        ++cnt;
        x>>=1;
    }
    for (int i=0;i<16;++i)num<<=1;
    cout<<num+x;
    return 0;
}

五、DEATHSTAR（位运算+模拟）

P8053 [COCI 2015/2016 #4] DEATHSTAR - 洛谷

因为题中是&操作后得到的数值，|=改行所有元素可以确保提取 满足改行情况的 该数可能的1的位置。

#include<bits/stdc++.h> 
using namespace std;
int n,a[1005][1005],ans[1005];
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cin>>a[i][j];
			ans[i]|=a[i][j];
		}
	}
	for(int i=0;i<n;i++)cout<<ans[i]<<" ";
	return 0;
}

六、A-B数对（排序+哈希）

P1102 A-B 数对 - 洛谷

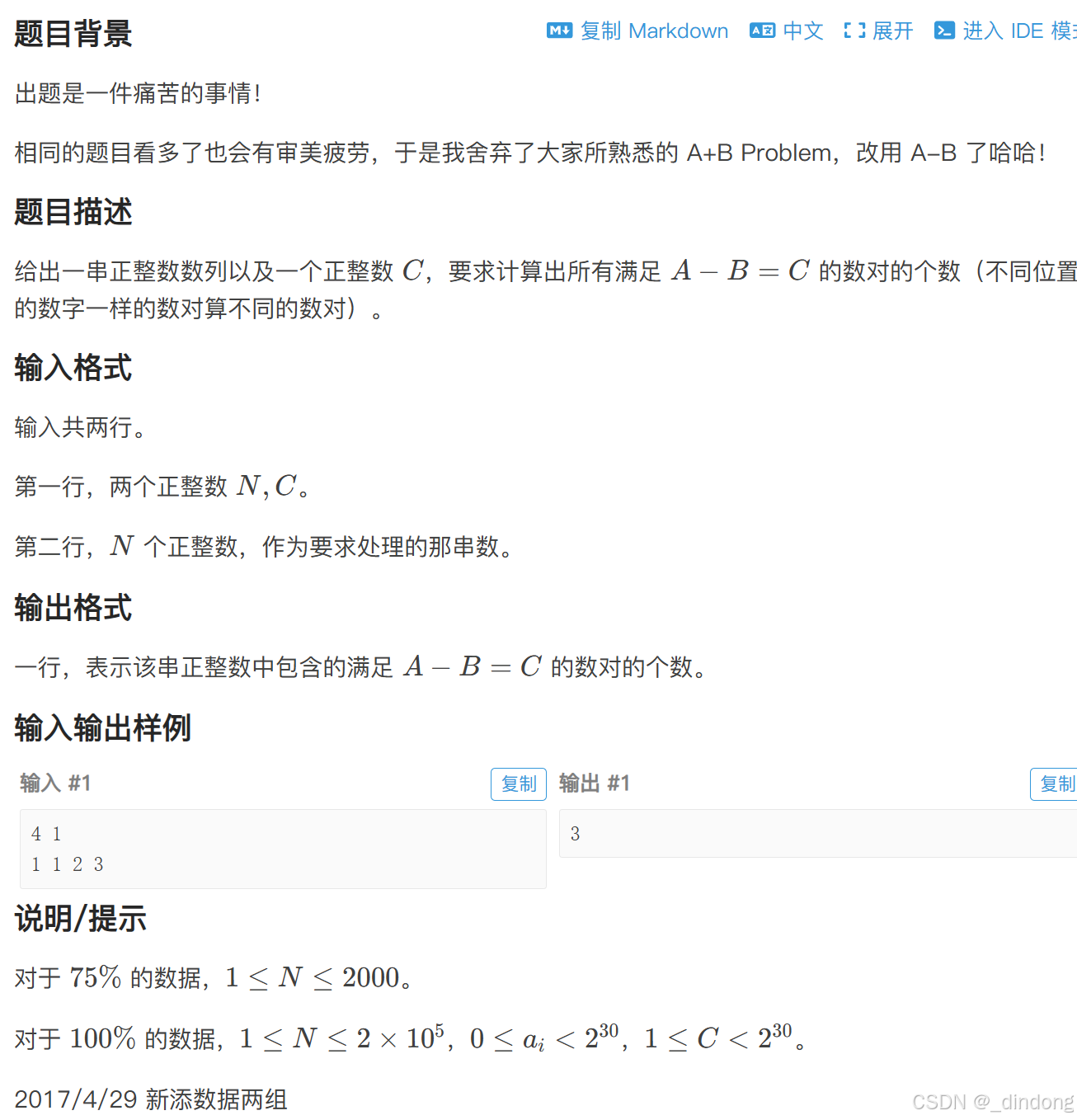
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=2e5+10;
ll arr[N],C;
int n;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    cin>>n>>C;
    unordered_map<ll,int> hash;
    for(int i=0;i<n;i++)cin>>arr[i];
    sort(arr,arr+n);
    ll ans=0;
    for (int i=0;i<n;i++)
    {
        ll x=arr[i];

        if (x-C>=0&&hash.count(x-C))ans+=hash[x-C];
        ++hash[x];

    }
    cout<<ans<<endl;
    return 0;
}

七、连续自然数和（暴力+简单优化 /  数学）

P1147 连续自然数和 - 洛谷

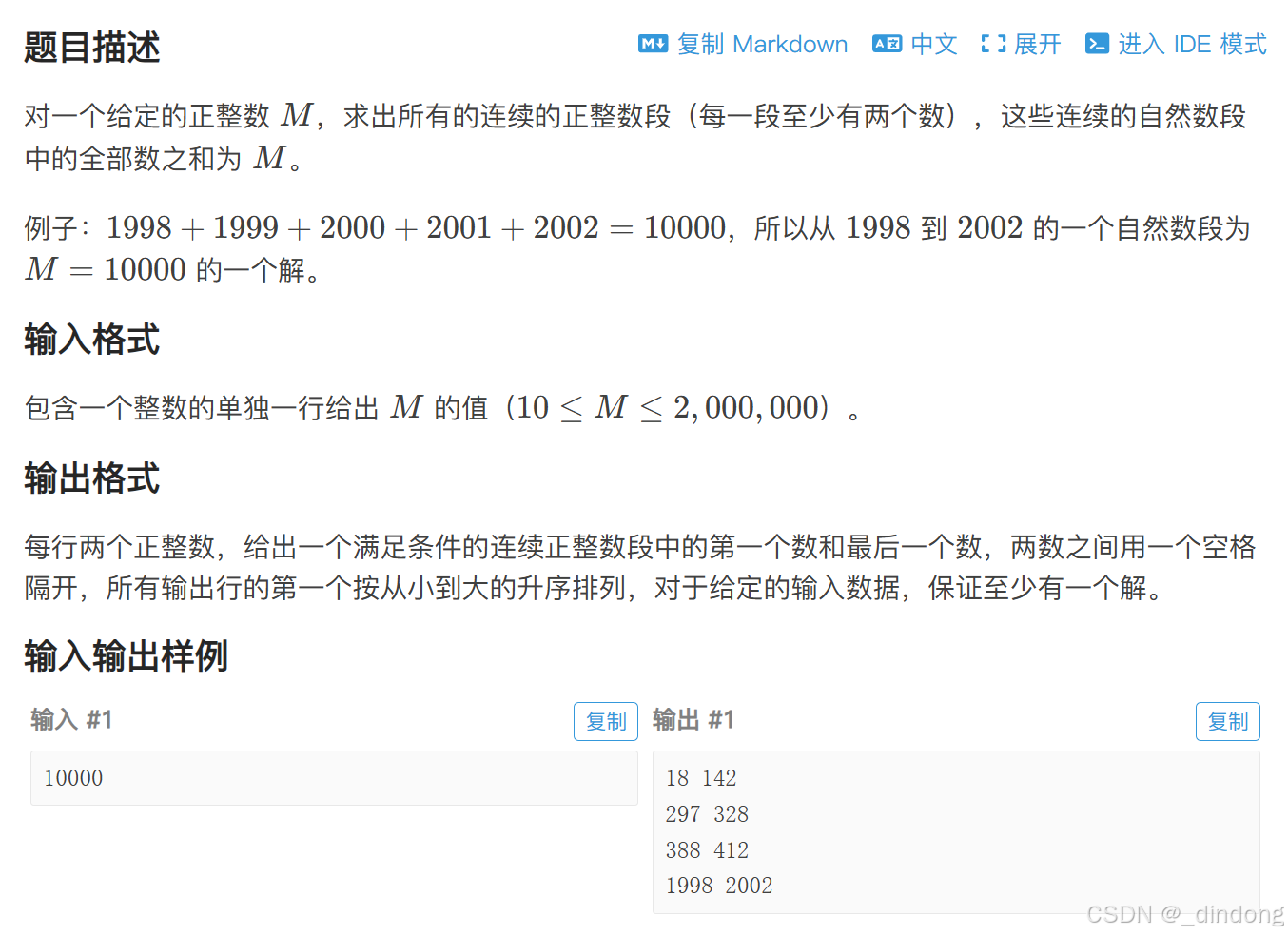
暴力+优化：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
int M;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    cin>>M;
    for (int i=1;i<=M/2;++i)
    {
        for (int j=i+1;j<=M;++j)
        {
            int sum=(i+j)*(j-i+1)/2;
            if (sum==M)cout<<i<<" "<<j<<endl;
            if (sum>M)break;
        }
    }
    return 0;
}

数学：说实话还是暴力+优化简洁易懂

#include<bits/stdc++.h>
using namespace std;
int m;
int main(){
    cin>>m;
    for(int k1=sqrt(2*m);k1>1;k1--)//枚举k1(注意是k1>1而不是k1>=1)
        if(2*m%k1==0 && (k1+2*m/k1)%2){//如果K2是整数而且与K1一奇一偶
            int k2=2*m/k1;
            cout<<(k2-k1+1)/2<<" "<<(k1+k2-1)/2<<endl;//输出答案
        }
    return 0;
}

八、在你窗外闪耀的星星（滑动窗口）

P3353 在你窗外闪耀的星星 - 洛谷

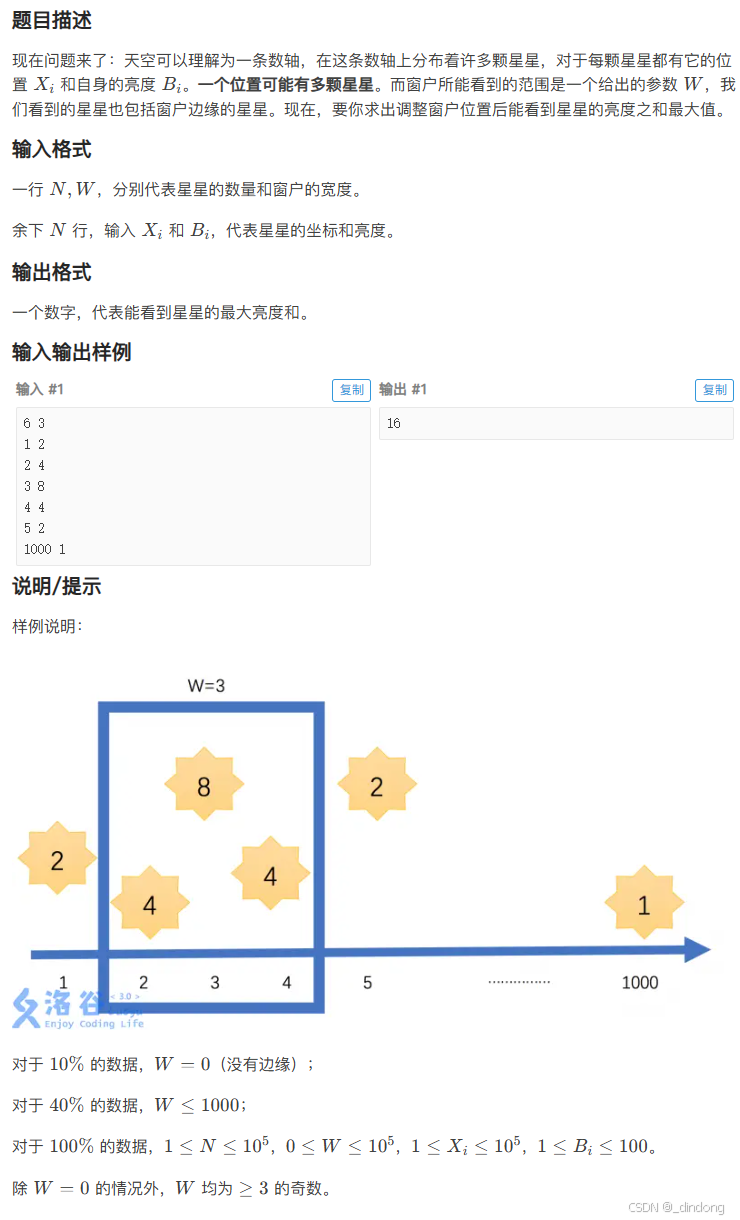
很经典的滑动窗口题，记得开ll

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
int n,W,x,b;
ll arr[N];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    cin>>n>>W;
    ll ans=0;
    int begin=N,end=0;
    while (n--)
    {
        cin>>x>>b;
        begin=min(begin,x);
        end=max(end,x);
        arr[x]+=b;
    }
    ll tmp=0;
    int left=begin,right=begin;
    while (right<=end)
    {
        while (right-left+1>W)
        {
            tmp-=arr[left];
            ++left;
        }
        tmp+=arr[right];
        ++right;
        ans=max(ans,tmp);
    }
    cout<<ans<<endl;
    return 0;
}

九、【模板】单调队列/滑动窗口

P1886 【模板】单调队列 / 滑动窗口 - 洛谷

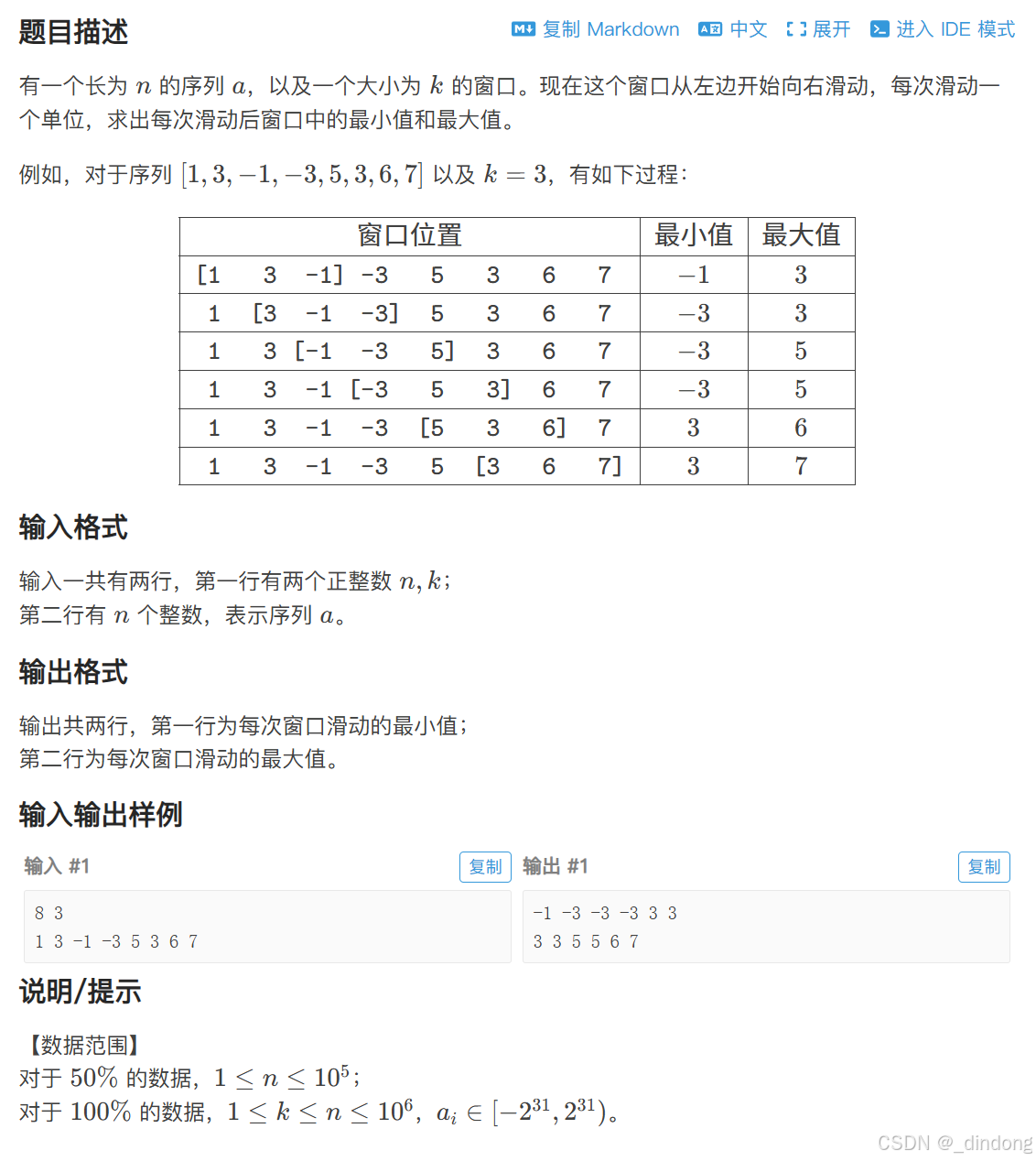
// #include <bits/stdc++.h>
#include <iostream>
using namespace std;

#define ll long long
#define endl '\n'
const int N=2e6+10;
int n,k,index[N],maxindex[N],minindex[N];
ll arr[N];
void work(int res[])
{
    int h=0,t=-1;
    for (int i=0;i<n;++i)
    {
        //队尾出队列
        while (t>=h&&arr[index[t]]>=arr[i])--t;
        //新元素入队列
        index[++t]=i;
        //左边界滑出窗口
        if (index[h]<i-k+1)++h;
        //队头就是最小
        if (i>=k-1)res[i-k+1]=index[h];
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    cin>>n>>k;
    for(int i=0;i<n;i++)cin>>arr[i];
    work(minindex);
    for (int i=0;i<n-k;++i)cout<<arr[minindex[i]]<<" ";
    cout<<arr[minindex[n-k]]<<endl;

    for (int i=0;i<n;++i)arr[i]=-arr[i];
    work(maxindex);
    for (int i=0;i<n-k;++i)cout<<-arr[maxindex[i]]<<" ";
    cout<<-arr[maxindex[n-k]]<<endl;
    return 0;
}

——————END——————